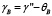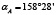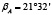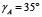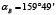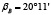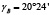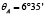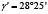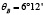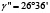Механические передачи широко распространены в современном машиностроении. Одной из разновидностей механических передач являются ременные передачи – старейшие передачи, которые применяются и в настоящее время в различных конвейерах, в приводах механизмов технологического и сельскохозяйственного оборудования, подъемниках, в строительной технике и прочих машинах. По сравнению с другими типами передач они обладают рядом особенностей, например: возможностью передачи движения на значительные расстояния; простотой конструкции; плавностью и бесшумностью работы; предохранением механизмов от резких колебаний нагрузки вследствие упругости ремня. У ременных передач существуют и недостатки. Основным недостатком ременных передач является повышенная нагрузка на валы и их опоры, связанная с большим предварительным натяжением ремня, поэтому при проектировании привода, содержащего одну или несколько ременных передач, необходимо уделять внимание конструированию опор.
Как правило, ременные передачи устанавливают на быстроходную ступень привода для связи электродвигателя с исполнительными механизмами, где вращающие моменты незначительные, что позволяет снизить радиальные габариты ременной передачи, а также ее себестоимость. Наряду с одноступенчатыми ременными передачами могут применяться многоступенчатые с большим передаточным отношением, позволяющие передавать вращающий момент на значительные расстояния, при этом исключая использование открытых зубчатых или цепных передач, но в таких случаях появляется необходимость проектирования различных опор с выбором варианта их расположения относительно двигательных установок и исполнительных устройств. Многовариантность решения такой задачи на этапе проектирования подразумевает использование различных CAD/CAE-программ. Например, авторы в источнике [1] приведено совершенствование методов проектирования технологического оборудования на современном этапе его развития с целью повышения эффективности конструирования с применением автоматизированных CAD/CAE/CAM-программ. Автор в статье [2] применяет CAD КОМПАС-3D и другие программы для усовершенствования конструкции клиноременной передачи привода технологического оборудования с целью повышения долговечности. Авторы в литературе [3] с помощью современных прикладных библиотек КОМПАС-3D излагают последовательность проектирования привода конвейера, который включает клиноременную передачу, с целью сокращения времени на подготовку производства и повышения экономической эффективности работы. В источнике [4] анализируется статическая прочность корпусного изделия с помощью CAE-модуля Simulation в программе SOLIDWORKS с целью выявления участков с минимальным и максимальным коэффициентом запаса прочности для разработки рекомендаций по созданию более рациональной конструкции в конкретных условиях эксплуатации. В работе [5] упоминается, что на этапе проектного расчета при поиске рациональной конструкции узла достаточно проводить статические расчеты прочности как менее трудоемкие с помощью метода конечных элементов, лежащего в основе CAE-программ.
В данной статье предлагается последовательность решения одной из множества задач по первичному проектированию ременного привода к какому-либо механизму, например конвейеру, которая может использоваться конструкторами при решении аналогичных задач на практике с использованием различных CAD-программ и дополнением твердотельных моделей необходимыми силовыми расчетами и исследованиями прочности в CAE-программе.
Цели исследования: изложение последовательности проектирования двухступенчатого ременного привода с расчетом силовых нагрузок в клиноременных передачах, построением годографа сил в промежуточном узле привода в зависимости от разного положения входного узла исполнительного механизма; анализ НДС твердотельных моделей двух исполнений наиболее нагруженной опоры из двух в промежуточном узле – с использованием для каждой задачи соответствующих современных CAD/CAE-программ.
Материал и методы исследования
При проектировании двухступенчатого ременного привода конвейера исходными данными являются кинематическая схема (рис. 1а) и другие параметры, которые однозначно позволяют определить кинематические и силовые факторы в передачах и валах привода.
Для решения задач такого типа наилучшим образом подходят прикладные библиотеки, встроенные в КОМПАС-3D [6], – это библиотеки «Каталог: Электродвигатели» и «Валы и механические передачи 2D». Исходными данными для такого расчета являются мощность двигателя Рдв = 3 кВт и частота вращения вала nдв = 690 об/мин, проектные передаточные числа ременных передач 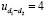 и
и 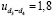 . С помощью первой библиотеки выбирают двигатель АИР 112МB8 У2 380 В, 50 Гц, IM1081 ТУ16-525.571-84, с помощью второй библиотеки производят геометрический и конструктивный расчет клиноременных передач (табл. 1), в том числе сопутствующих узлов и деталей, на которых установлены шкивы (рис. 1б).
. С помощью первой библиотеки выбирают двигатель АИР 112МB8 У2 380 В, 50 Гц, IM1081 ТУ16-525.571-84, с помощью второй библиотеки производят геометрический и конструктивный расчет клиноременных передач (табл. 1), в том числе сопутствующих узлов и деталей, на которых установлены шкивы (рис. 1б).
По построенным двумерным эскизам получают в автоматическом режиме трехмерные твердотельные модели (шкивы, валы, втулки (рис. 1б)) и при необходимости разрабатывают конструкторскую документацию, используя рассчитанные данные. Подшипники опор промежуточного вала – UC207 (ISO), входного вала конвейера – UC210. Корпус опоры подшипника принят типа UCPH (ISO) – вертикальная опора с пьедесталом (рис. 1б).
Следующим этапом необходимо произвести оценку силовых нагрузок в клиноременных передачах. Формулы для оценки сил приведены в литературе [7] и ГОСТ 1284.3-96, можно также рассчитать с помощью программного обеспечения, например [8].
Таблица 1
Рассчитанные параметры клиноременных передач двухступенчатого привода с помощью прикладных библиотек КОМПАС-3D, ГОСТ 1284.1-89, ремень кордшнуровой
|
Параметр ременной передачи |
Передача №1, i = A |
Передача №2, i = B |
|
Обозначение ремня |
А |
B |
|
Количество ремней в передаче ki , шт. |
3 |
2 |
|
Диаметр меньшего шкива, мм |
d1 = 80 |
d3 = 280 |
|
Диаметр большего шкива, мм |
d2 = 315 |
d4 = 500 |
|
Линейная скорость ремня vi , м/с |
2,889 |
2,542 |
|
Длина ремня, мм |
1900 |
2500 |
|
Действительное передаточное число |
3,977 |
1,804 |
|
Межцентровое расстояние, мм |
629 |
628 |
|
Окружное усилие в передаче Fti, Н |
1038,5 |
1109,2 |
|
Допускаемая передаваемая мощность [P], кВт |
3,105 |
3,249 |
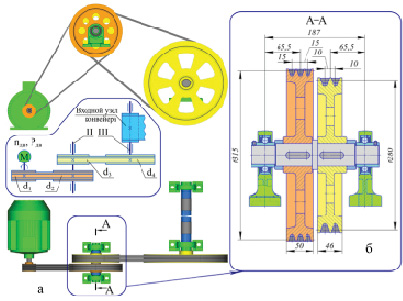
Рис. 1. Двухступенчатый привод конвейера с двумя клиноременными передачами
Согласно сведениям в ГОСТ 1284.3-96, предварительное натяжение ветви одного ремня F0i для передач с закрепленными центрами определяют по формуле:
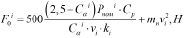 (1)
(1)
где Pномi – номинальная мощность, кВт, PномA = 3 кВт, PномB = 2,819 кВт, mn – погонная масса ремня по ГОСТ 1284.1-89, кг/м, Cαi – коэффициент угла обхвата, CαA = 0,946, CαB = 0,95, Cp = 1 – коэффициент динамичности нагрузки и режима работы при односменной работе, vi , ki (табл. 1).
Вычисляют предварительное натяжение ветви комплекта ремней в передачах 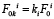 . Рассчитывают коэффициент тяги
. Рассчитывают коэффициент тяги 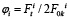 и параметр
и параметр 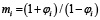 , где Fti – окружное усилие в передаче, Н. Определяют силы натяжения ведущей
, где Fti – окружное усилие в передаче, Н. Определяют силы натяжения ведущей 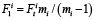 и ведомой
и ведомой 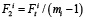 ветвей комплекта ремней (рис. 2а), равнодействующие силы на промежуточный вал от сил натяжения ведущей и ведомой ветвей комплекта ремней для каждой передачи Fri и от двух передач в приводе FR (рис. 2б).
ветвей комплекта ремней (рис. 2а), равнодействующие силы на промежуточный вал от сил натяжения ведущей и ведомой ветвей комплекта ремней для каждой передачи Fri и от двух передач в приводе FR (рис. 2б).
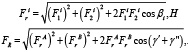 (2)
(2)
Схема распределения сил, действующих на промежуточный вал и его опоры, показана на рисунке 2, причем положение узлов привода выбрано таким образом, чтобы результирующая сила FR действовала вертикально, то есть горизонтальные координаты векторов сил равны между собой FrAsin γ' = FrBsin γ'' (рис. 2б). Такое расположение достигается уточнением угла γB через заданный угол γA с определением угла γ'' через силовые соотношения координат векторов, действующих по горизонтали. Остальные углы можно определить математическими методами или использовать модуль параметризации, встроенный в современные CAD-программы, например T-Flex CAD [9], КОМПАС-3D [10]. Рассчитанные данные по формулам выше и с использованием параметризации в одной из CAD-программ приведены в таблице 2.
Таблица 2
Рассчитанные силовые и угловые параметры ременных передач (рис. 2)
|
Параметр |
Передача №1, i = A |
Передача №2, i = B |
|
Предварительное натяжение ветви ремня F0i, Н |
F0A = 285,1 |
F0B = 453,5 |
|
Предварительное натяжение ветви комплекта ремней в передачах F0ki, Н |
F0kA = 855,3 |
F0kB = 907,0 |
|
Силы натяжения ведущей F1i и ведомой F2i ветвей комплекта ремней, Н |
F1A = 1374,7 F2A = 336,2 |
F1B = 1462,3 F2B = 353,1 |
|
Равнодействующие силы комплекта ремней Fri, Н |
FrA = 1692,0 |
FrB = 1798,0 |
|
Равнодействующая сила FR , Н |
FR = 3095,8 |
|
|
Углы в передачах (рис. 2а, 2б), где |
|
|
|
Углы, определяющие направления сил для заданного положения (рис. 2б) |
|
|
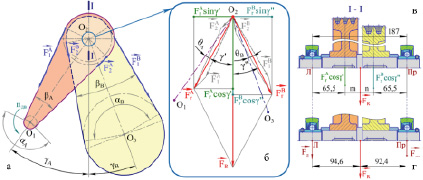
Рис. 2. Распределение сил в промежуточном узле ременного привода
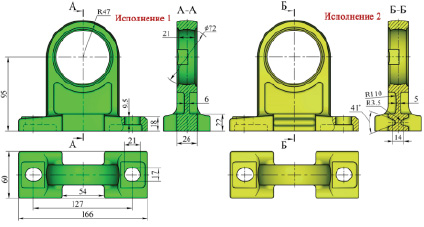
Рис. 3. Рассчитываемые исполнения корпуса опоры подшипника типа UCPH (ISO)
Для определения силовых нагрузок в левой Fл и правой Fпр опорах промежуточного вала необходимо вычислить расстояния m и n через уравнение моментов координат векторов результирующих сил комплекта ремней 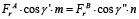 относительно точки приложения силы FR и соотношения длин в поперечном сечении узла промежуточного вала (рис. 2в): m = 29,1 мм и n = 26,9 мм. Из уравнений для определения равнодействующей в системе параллельных сил (рис. 2г) определяем силовые нагрузки в опорах: Fл = 1530 Н, Fпр = 1566 Н. Более нагружена правая опора (рис. 2г), принимаем ее в дальнейший расчет.
относительно точки приложения силы FR и соотношения длин в поперечном сечении узла промежуточного вала (рис. 2в): m = 29,1 мм и n = 26,9 мм. Из уравнений для определения равнодействующей в системе параллельных сил (рис. 2г) определяем силовые нагрузки в опорах: Fл = 1530 Н, Fпр = 1566 Н. Более нагружена правая опора (рис. 2г), принимаем ее в дальнейший расчет.
В одной из CAD-программ спроектирована в двух исполнениях твердотельная модель корпуса вертикальной опоры подшипника с пьедесталом типа UCPH (ISO) для сферического шарикоподшипника UC207 (ISO) с посадочным диаметром 35 мм (рис. 3), используемая в промежуточном узле привода. Отличия исполнений опор заключаются в разной толщине и форме тонкой стенки, также нижняя перемычка при одинаковом габарите во втором исполнении имеет две выемки, что позволило при равных габаритных и присоединительных размерах рассматриваемых опор снизить массу опоры на 5% во втором случае.
Для оценки НДС в статической постановке с помощью метода конечных элементов опор с точной геометрией (рис. 3) использован CAE-модуль Simulation в программе SOLIDWORKS, который позволяет точно и быстро производить решение сложных задач [11].
В расчетах численными методами применены ограничения и нагрузки, которые отражают реальную работу узла с учетом допущений: не рассматривались погрешности изготовления и неточности монтажа, использовался однородный и изотропный материал корпуса опоры – серый чугун марки СЧ15, моделировался линейной, упругой, изотропной моделью поведения материала, характеризующейся модулем Юнга и коэффициентом Пуассона. Ограничения в модели: фиксация опорной поверхности опоры с целью исключения вертикальных перемещений; ограничение с нулевым перемещением в горизонтальных направлениях отверстий под болты. Такой набор ограничений позволяет учесть крепление опоры к раме привода. Подшипник в модели является жестким, деформации не рассматриваются. Граничные условия для контактирующих поверхностей (внутренняя сферическая поверхность корпуса опоры и наружная поверхность подшипника Ø72 мм) – «нет проникновения». Радиальная нагрузка величиной Fпр = 1566 Н приложена к внутренней посадочной поверхности подшипника Ø35 мм в ее нижней части на дуге 180º, распределение синусоидальное. Далее произведено построение тетраэдральной конечно-элементной сетки на основе кривизны поверхности, что позволило в местах плавных переходов поверхностей сделать сетку меньшего размера. Максимальный размер стороны элемента сетки составил 2 мм, минимальный – 1 мм. Число объемных конечных элементов в исполнении А – 321,486 тыс., в исполнении Б – 320,620 тыс.
Результаты исследования и их обсуждение
С использованием параметризации в одной из CAD-программ по данным выше произведено построение годографа результирующей силы FR при различных положениях входного узла исполнительного механизма – точка OЗj , где j – номер положения опоры (рис. 4). С помощью годографа сил можно выбирать необходимое расположение узлов и опор привода с целью выбора силовой нагрузки, отвечающей различным критериям, например: сила FR действует только вертикально (рис. 2) – точка OЗj находится в положении 1 (рис. 4), тогда опорную поверхность корпуса опоры (рис. 3) в точке O2 можно расположить горизонтально, так, чтобы опора воспринимала преимущественно нагрузки сжатия; сила FR отклонена на угол 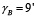 от линии центров опор и достигает своего минимального значения, причем линии центров передач образуют угол 180º – точка OЗj находится в положении 5 (рис. 4). Для остальных положений входного узла исполнительного механизма по отношению к двигателю значения силы FR и углов γB, γA сведены в таблицу 3.
от линии центров опор и достигает своего минимального значения, причем линии центров передач образуют угол 180º – точка OЗj находится в положении 5 (рис. 4). Для остальных положений входного узла исполнительного механизма по отношению к двигателю значения силы FR и углов γB, γA сведены в таблицу 3.
Произведен анализ напряженно-деформированного состояния двух исполнений корпуса опоры с помощью CAE-модуля Simulation в программе SOLIDWORKS с определением напряжений фон Мизеса (von Mises), где результаты расчета в виде картин распределения напряжений представлены на рисунке 5. Напряжения достигают своей максимальной величины в месте соединения тонкой стенки с обоймой опоры корпуса подшипника в обоих исполнениях. Немного видоизменив конструкцию опоры во втором ее исполнении, удалось уменьшить величину максимальных напряжений на 10% (рис. 5).
Таблица 3
Сила FR и углы в зависимости от положения опоры OЗj относительно O1 (рис. 4)
|
Параметр |
j = 0 |
j = 1 |
j = 2 |
j = 3 |
j = 4 |
j = 5 |
j = 6 |
j = 7 |
j = 8 |
|
Сила FR, Н |
3489,8 |
3095,8 |
2477,0 |
1624,4 |
626,2 |
106,7 |
1043,3 |
2235,8 |
3090,6 |
|
Угол γA, рад |
0,111 |
0,611 |
0,997 |
1,260 |
1,675 |
3,144 |
1,251 |
0,789 |
0,384 |
|
Угол γB, рад |
0,111 |
0,356 |
0,644 |
0,921 |
1,117 |
0,003 |
1,280 |
0,984 |
0,576 |
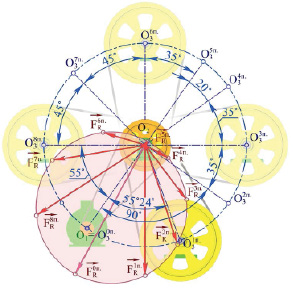
Рис. 4. Годограф результирующей силы FR при разных положениях входного узла исполнительного механизма
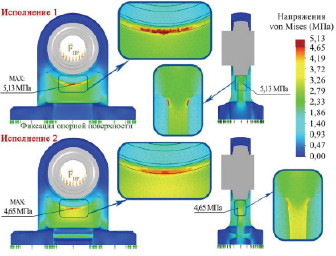
Рис. 5. Распределение напряжений в рассчитываемых опорах подшипника
В узлах, где наблюдаются максимальные напряжения по Мизесу (рис. 5), третье главное напряжение (максимальное из всех главных напряжений) также достигает своих максимальных величин: для исполнения 1: σ3 = –5,24 МПа, для исполнения 2: σ3 = –4,61 МПа (рис. 3, 5). С учетом того, что для чугуна предел прочности при сжатии в несколько раз превышает предел прочности при растяжении, который согласно ГОСТ 1412-85 должен быть не менее 150 МПа, получаем достаточный запас прочности при работе опоры как в условиях сжатия, так и при растяжении.
Заключение
На проектном этапе перед конструктором возникают многовариантные задачи по рациональному выбору и расчету узлов проектируемого механизма привода. Одной из таких задач является выбор программного обеспечения, которое позволяет полностью спроектировать механизм, включая силовой расчет и оценку НДС. Большинство современных CAD/CAE-программ могут быть использованы для полного цикла проектирования механизма привода, но в некоторых программах более детально проработаны некоторые модули, которые позволяют максимально упростить рутинные операции конструктора или снизить трудозатраты при проведении прочностных расчетов, а также использовать встроенную параметризацию как один из вариантов поиска рационального решения расположения узлов и механизмов привода друг относительно друга.
В данной статье изложен один из множества вариантов реализации механизма привода при его проектировании к какому-либо механизму, например конвейеру. Основная задача конструктора на стадии проектирования – это выбор последовательности действий, четкое понимание готового варианта решения поставленной задачи. Например, изменив положение узлов друг относительно друга, можно варьировать силовые факторы и, как следствие, уменьшить металлоемкость узла и снизить его себестоимость. Проведя прочностные расчеты твердотельных моделей с помощью CAE-программ или модулей, можно разработать более рациональную конструкцию узла. Приведенная последовательность проектирования привода дополняет классические методы расчета в соответствии с различными рекомендациями и нормами, а также позволяет сконструировать надежный узел с минимальными массово-экономическими затратами в производстве, эксплуатации и ремонте.




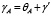 ,
,