Оптимальная организация дорожного движения в режиме реального времени – актуальная проблема. С учетом современных технологий это возможно в рамках интеллектуальных транспортных систем. Поэтому важной и своевременной задачей является математическое моделирование транспортных и пешеходных потоков. Для оперативного реагирования на постоянно изменяющуюся ситуацию на улично-дорожной сети требуется минимизация времени между получением исходных данных задачи и параметров, являющихся результатом ее решения. С этой точки зрения наиболее подходящими являются математические модели, основанные на аналитическом решении поставленных задач.
Для моделей транспортных и пешеходных потоков существует аналогичная классификация. Их традиционно по степени детализации используемых параметров разделяют на макроскопические, мезоскопические и микроскопические [1–4]. Микроскопические модели основаны на учете движения каждого отдельного пешехода; мезоскопические учитывают поведение отдельных пешеходов, но с целью определения параметров всего потока или закона распределения потока; макроскопические определяют характеристики потока в целом без учета поведения отдельных участников движения. Для решения транспортных задач различного уровня (локальных или глобальных) требуются различные типы моделей потоков.
Целью данной работы является разработка метода определения характеристик пешеходного потока в режиме реального времени в рамках интеллектуальных транспортных систем.
Материалы и методы исследования
Для того, чтобы учитывать движение пешеходов при организации движения в узловых точках сети в режиме реального времени, удобно применять мезоскопическое моделирование. В данном случае необходимо оценивать задержки транспортных средств, вызванные необходимостью пропускать пешеходные потоки. Кроме того, при выборе оптимальной схемы организации движения на конкретном перекрестке следует также учитывать потери времени пешеходов [5]. В случае направленного движения пешеходов к переходу удобно применять модели, описывающие поток как случайный процесс с помощью случайных функций. При таком подходе возможно разработать аналитический аппарат для оценки средних потерь времени всех конфликтующих потоков (как транспортных, так и пешеходных) [6, 7] с помощью методов теории массового обслуживания и теории восстановления. В работе N. Bode [8] утверждается, что интервалы по времени между подряд идущими пешеходами имеют гамма-распределение, частным случаем которого является специальное распределение Эрланга.
В работах [8–10] обращается внимание на то, что значительное влияние на характеристики пешеходного потока оказывает их разделение на малые социальные группы. В данной работе с этой целью малые социальные группы будут определяться как отдельные кластеры. При моделировании пешеходного потока используется такой же подход, который применялся автором при разработке модели транспортных потоков TIMeR_Mod [11].
Под событием в модели понимается прибытие очередного объекта к фиксированной точке пространства. Интервалы по времени между отдельными событиями будем считать подчиненными двупараметрическому закону Эрланга. Под объектом понимается либо отдельный пешеход, либо кластер пешеходов – плотное скопление людей (как правило, знакомых, следующих в одинаковом направлении). В работе автора [12] был предложен один из возможных алгоритмов разбиения пешеходов на кластеры. Предлагалось формировать кластеры, проверяя выполнение условия dij < dfree , где dij – расстояние от точки с текущими координатами до центра кластера, dfree – максимально допустимое расстояние, определяющее границу между свободным движнием пешеходов и их движением в связанной группе.
Исходные данные для определения параметров пешеходного потока предполагается получать с камер видеонаблюдения. В настоящей работе метод автоматической работы с камерами видеонаблюдения не рссматривается, это является задачей отдельного исследования. Исходными данными являются декартовы координаты пешехода в фиксированный момент времени. Кроме этого необходимо фиксировать время пересечения последовательно движущимися объектами заданной точки пространства.
Для расчета исходящих параметров (характеристик пешеходного потока) будут применяться методы теории случайных функций, теории восстановления [13, 14].
Результаты исследования и их обсуждение
1. Моделирование пешеходного потока как потока кластеров
Для определения взаимного влияния пешеходных и транспортных потоков на перекрестках, необходимо однотипно моделировать их движение. В этом случае можно использовать методы определения средней очереди в потоке на перекрестке, средней задержки на перекрестке по направлениям, используя методы и аналитический аппарат, который был разработан автором для модели TIMeR_Mod [15].
Если рассматривать эту частную задачу, то координаты объектов – пешеходов можно брать одномерные, спроецированные на ось движения. То есть это точки в одномерном пространстве. Основной признак, по которому будем объединять объекты – расстояние между двумя точками. Кроме того, следует ввести ограничение на расстояние между соседними объектами.
Кластером в данном случае будем считать множество точек S, расстояние от каждой из которых хотя бы до одной точки этого множества S меньше некоторого заданного значения dfree.
Разработана программа в среде DELPHI, реализующая разбиение потока на кластеры.
Описание программы разбиения потока на кластеры
Функция DPOINT получает на вход координаты точек и выдаёт расстояние между ними.
Функция Counter получает на вход массив данных и количество точек. Если ни одна из точек не принадлежит ни одному из кластеров, то счётчик увеличивается на единицу.
Процедура MakeUpClaster получает на вход критическое расстояние между точками, начальную точку кластера, количество точек, номер кластера и исходный массив данных.
Проверяем расстояния от всех точек до начальной с помощью функции DPOINT; если расстояние не более чем dfree., то группируем эти точки в один кластер.
Основная программа начинается при нажатии кнопки Start.
Заполняем массив данных MainArr координатами объектов – пешеходов (MainArr – матрица размеров 3 × N).
Формируем первый кластер:
− задаем начальную точку; проверяем, какие точки из MainArr находятся от исходной на расстоянии не более чем dfree. Если это условие выполнено, то мы группируем эти точки в один кластер. Это будет кластер № 1.
Формируем остальные кластеры:
− увеличиваем номер кластера на единицу;
− пока функция Counter > 0, находим точку из MainArr, не принадлежащую ни одному кластеру;
− формируем кластер, считая найденную точку начальной, с помощью процедуры MakeUpClaster.
В результате работы программы разбиение на кластеры задается однозначно с точностью до порядка нумерации кластеров. Действительно, пусть Pi – некоторая точка из кластера K1, Pj – произвольная точка.
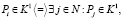
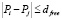. (1)
Предположим, что точка Pl принадлежит одновременно кластерам Ks и Kt и, следовательно:
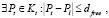
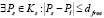. (2)
По алгоритму разбиения на кластеры получаем, что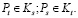 
Рассуждая аналогичным образом по поводу остальных точек кластеров Ks и Kt, получим, что все точки из Ks ⊂ Kt и все точки из Kt ⊂ Ks . Таким образом, эти кластеры совпадают: Ks = Kt. То есть если точка принадлежит двум разным кластерам, то эти кластеры совпадают.
На рис. 1 представлен пример работы программы.
Замечание: если расстояние между большей частью объектов – пешеходов меньше контрольного расстояния dfree, то разбиение на кластеры нецелесообразно, так как грубо аппроксимирует поток. В этом случае будем рассматривать интервалы по времени не между центрами кластеров, а между отдельными пешеходами. Согласно исследованиям в теории пешеходных потоков в этом случае интервалы по времени в плотном пешеходном потоке подчинены нормальному распределению. При значении параметра k ≥ 5 специального распределения Эрланга он близок к нормальному.
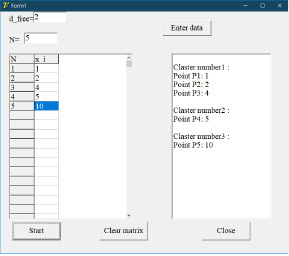
Рис. 1. Пример работы программы разбиения пешеходов на кластеры
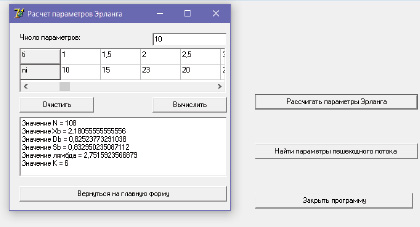
Рис. 2. Пример работы программы расчета параметров Эрланга
2. Определение параметров Эрланга для пешеходного потока
Для определения параметров распределения Эрланга, которым аппроксимируется пешеходный поток, необходимо получить соответствие между значением интервалов по времени между следующими друг за другом объектами в потоке и количеством таких интервалов. Уточним, что при разбиении потока на кластеры фиксируется прохождение центром кластера заданной точки пространства.
Тогда параметры распределения Эрланга определяются по формулам
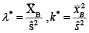, (3)
где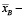 
выборочная средняя случайной величины T (интервалов между следующими подряд пешеходами);
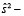исправленная выборочная дисперсия случайной величины T.
В общем случае получаем нецелое k. Для того, чтобы получить параметры распределения Эрланга, в качестве k возьмём k = [k*] + 1, а в качестве параметра λ следующее значение:
.
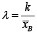Согласно проведенным экспериментам (видеосъемка потоков) при разбиении на кластеры пешеходного потока с низкой и средней интенсивностью движения значение параметра k = 1 или k = 2. При высокой интенсивности движения разбиение на кластеры нецелесообразно, пешеходный поток хорошо аппроксимировался законом Эрланга при значении параметра k = 6. Если разбиение на кластеры не проводилось, в потоках с низкой и средней интенсивностью параметр k принимал значения от одного до четырех. Адекватность гипотезы о виде распределения проверялась с помощью критериев Пирсона и Романовского. С целью расчета параметров распределения Эрланга написана программа (рис. 2) .
3. Применение математической модели для определения характеристик пешеходных потоков у перекрестков
В работе автора [11] приведен вывод аналитического аппарата для определения таких характеристик потока, как средняя длина очереди, средняя суммарная задержка в узловой точке, средняя задержка одного объекта в потоке при значениях параметра k от одного до четырех. Точный аналитический аппарат для определения характеристик пешеходных потоков у перекрестков с помощью теории восстановления [13] возможно получить также для k = 6. Ниже приведено соответствующее утверждение, доказанное авторами.
Теорема 1: пусть распределение интервалов по времени между событиями в потоке представляет собой специальный поток Эрланга с параметрами k и λ. Тогда число объектов, пересекающих данную точку пространства в течение промежутка времени (0; t), для k = 6 может быть оценено по формуле
.
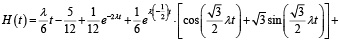
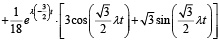При слиянии s пешеходных потоков Эрланга с параметрами k и λi , i = 1,2,…,s количество пешеходов, пересекающих данную точку пространства в течение промежутка времени (0; t), может быть оценено по формуле
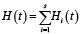. (4)
Авторами доказано, что такие характеристики, как средняя суммарная задержка требований и средняя задержка одного пешехода, могут быть рассчитаны так, как утверждается в Теореме 2.
Теорема 2: пусть распределение интервалов по времени между событиями в потоке представляет собой специальный поток Эрланга с параметрами k и λ. Тогда:
− средняя суммарная задержка требований рассматриваемого потока за время Ti секунд, в течение которого запрещено движение в данном направлении, может быть оценено по формуле
;
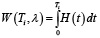− средняя задержка (в секундах) одного пешехода за время Ti секунд, в течение которого запрещено движение в данном направлении, может быть рассчитана по формуле
.
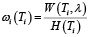Авторами разработаны соответствующие программные модули для расчета параметров пешеходного потока (рис. 3).
Заключение
Моделирование пешеходных потоков приобрело большую значимость в последнее время для таких отраслей, как организация дорожного движения, строительство зданий и сооружений. С помощью моделирования движения потоков пешеходов прогнозируют среднее время эвакуации, среднюю величину задержек объектов в тех или иных ситуациях, среднюю длину очереди при перекрытом движении. Особенно актуально получение таких характеристик в режиме реального времени и с достаточной степенью точности, так как это дает возможность оперативно реагировать на изменяющуюся ситуацию. Результаты представленной работы отвечают этим целям и могут быть использованы в интеллектуальных транспортных системах.
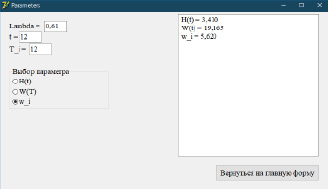
Рис. 3. Пример работы программы определения характеристик пешеходного потока