Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Динамическое развитие горной промышленности предполагает повышение требований к подготовке выпускников горных вузов, работа которых связана с обработкой информации, полученной в результате изучения горных пород и их массивов, разнообразных инженерных экспериментов. Критическое мышление в данном случае – важнейший фактор при восприятии и обобщении поступающих данных.

В научной литературе существует большое количество определений понятия «критическое мышление».

Б. Рассел под критическим мышлением понимает «процесс оценки или категоризации в терминах ранее приобретенных базовых знаний... оно включает в себя установку, плюс владение фактами, плюс ряд навыков мышления» [1, с. 134]. Как видно из определения, важным компонентом критического мышления является установка, готовность к критическому мышлению.

Дж. Дьюи определяет критическое мышление как рефлексивное мышление и приравнивает его к интеллектуальному (только оно имеет педагогическую ценность), важная функция которого – разрешение сомнений. Автор выделяет этапы рефлексивного мышления: «состояние нерешимости, колебания ума или сомнения; процесс поиска, исследования, направленный на то, чтобы осветить дальнейшие факты, служащие для подтверждения или отрицания вызванного мнения» [2, с. 7].

К.П. Кокарев, анализируя определения критического мышления, отмечает одно необходимое условие, наличие которого позволяет говорить о развитом критическом мышлении – это «умение распознавать ситуации, в которых нужно останавливать автоматизм и начинать мыслить критически» [3, с. 20]. Автор отмечает, что «наше мышление в жизни не решает сложных задач – поэтому не особенно трудозатратно. В отличие от него аналитическое мышление требует больших ресурсов – и поэтому используется редко. Критическое мышление играет роль «переключателя» типов мышления: умение в нужное время перейти к аналитическому мышлению, сделать обоснованные выводы, оценить последствия исполнения своих решений» [3, с. 20].

Д.А. Шаров пишет: «Критическое мышление отражает в себе направленность на улучшение собственного мышления. Другими словами, оно есть средство саморегуляции мышления с целью его оптимизации в процессе решения возникающих проблем. Именно критическое мышление приходит на помощь, когда проблема не решается, когда необходимо вычленить фундаментальные основания принятого решения, и именно критическое мышление помогает выявить в нем ошибки и внутренние противоречия» [4, с. 215]. Наличие противоречий не позволяет формировать целостное представление об исследуемом предмете (процессе) для получения полного знания о нем. Человек в своем познании окружающего мира стремится приблизиться к абсолютной истине. Причем сам процесс движения происходит поэтапно. На каждом этапе с помощью критического мышления человек «осознает и выявляет грань между познанным и непознанным, устанавливает связи не только внутри непознанного, но и выходы из познанного в непознанное» [5].

Под критическим мышлением мы понимаем «мыслительный процесс, позволяющий осуществлять оценочно-рефлексивную деятельность, направленную на оптимальное решение проблемной ситуации при ее всестороннем критическом анализе с помощью знаний, опирающихся на субъектный опыт, и с помощью аргументированного обоснования (опровержения) истинности выдвигаемых гипотез, построенных на законах логики для последующей всесторонней оценки последствий возможных решений» [6, с. 68].

Формированию критического мышления студентов вузов в процессе обучения математике посвящены работы А.А. Вендиной [7], Н.В. Сухановой [8], Л.И. Якобюк [9]. Анализ вышеперечисленных работ показал, что при формировании критического мышления в процессе обучения математике в вузах не учитывается использование профессиональной области знаний, в которой можно задействовать математический аппарат. Таким образом, появилась необходимость в разработке методики обучения математике студентов горных вузов с целью формирования у них критического мышления, основанной на анализе, оценке, опровержении информации из сферы будущей профессиональной деятельности. Это позволит им принимать обоснованные управленческие решения, на основании которых полученные результаты можно будет применить на практике – безопасно и эффективно использовать горные территории и ресурсы.

Цель исследования – разработка методики формирования критического мышления в процессе обучения математике студентов горных вузов.

Материалы и методы исследования

Самостоятельная познавательная деятельность является отличительной чертой критического мышления. Основываясь на этом, мы выделили в качестве обязательных следующие принципы формирования критического мышления студентов: активного взаимодействия, творчества, опоры на субъектный опыт, принцип управляемого перехода от деятельности в учебной ситуации к деятельности в профессиональной ситуации. Особенность выделенных принципов состоит в обеспечении рабочей обстановки, которая создаст благоприятные условия для активной, самостоятельной сознательной работы студентов, что приведет к всестороннему рассмотрению решаемой проблемной ситуации с последующей оценкой своих действий и действий других. Полученные в результате знания составят личный опыт студентов, который можно будет применить в будущей профессиональной деятельности.

Для формирования критического мышления у студентов горных вузов мы предлагаем использовать прикладные задачи, в сюжете которых находится реальная профессиональная ситуация из области горного дела, представленная в виде информационной составляющей, структурируя которую студенты смогут проанализировать предлагаемые обстоятельства, понять специфику проблемы, требующую решения (всесторонний критический анализ), разработать варианты ее разрешения и выделить оптимальный из них (оценка) [10].

Работа над решением задач предполагает выдвижение гипотез. Это может привести к появлению противоречивых предположений относительно, например, правильности построения математической модели исследуемого процесса горного дела. В результате активной мыслительной деятельности студенты смогут аргументированно обосновывать или опровергать истинность выдвигаемых гипотез, что приведет к разрешению появившихся противоречий и формированию критического мышления.

Мы предлагаем такие прикладные задачи, в результате решения которых получается, что две совершенно разные модели описывают один исследуемый процесс горного дела. Возникает противоречие, разрешить которое возможно после сравнения результатов решения. Становится очевидным, что одна из моделей точнее описывает исследуемый процесс. Особенность данных задач – подготовить студентов к тому, что в процессе критического осмысления проблемной ситуации первоначально собранная информация об исследуемом объекте может подтверждаться, дополняться или вообще оказаться недостоверной.

В конце решения задач происходит рефлексия собственной деятельности. Студентам предлагается заполнить карту самоанализа, в которой прописаны возможные затруднения при решении прикладных задач. Учащиеся отмечают те позиции, которые вызвали затруднения. При возникновении затруднений, не вписанных в таблицу, студенты самостоятельно заполняют пустые строки.

Применение прикладных задач в обучении позволяет не только включить в личный опыт базовые предметные знания и умения, но критически их переосмыслить для будущего использования в работе с новейшими процессами и технологиями. Это поможет обойти быстрое «устаревание» предметных знаний и умений [11].

Для выявления уровня сформированности критического мышления нами введены показатели критического мышления, представленные в табл. 1.

На начальном этапе экспериментальной работы со студентами 1 курса (семестр 1) проводились практические занятия, на которых проходило решение прикладных задач как в индивидуальной, так и групповой форме. В качестве методов эксперимента были выбраны опрос, беседы, наблюдение, проведение контрольных работ, в состав которых входили прикладные задачи. Анализ полученных результатов позволил нам выявить уровни владения студентами выделенными показателями критического мышления. Результаты исследования, проведенного в начале экспериментальной работы, представлены в табл. 1.

Анализ данных позволил выявить проблемы, связанные с неумением студентов искать недостающую для решения задач информацию, выявлять избыточную, низкий уровень умений, связанных с выдвижением, аргументацией, опровержением гипотез, с исследованием моделей реальных процессов горного производства. Для исправления этой ситуации нами предложены приемы формирования критического мышления студентов.

Таблица 1

Показатели критического мышления

Таблица 2

Схема ориентирования

1. Использование схем ориентирования поможет студентам определить систему базовых знаний математического и профессионально-прикладного материала, позволяющих решить задачу. Вид схемы ориентирования представлен в табл. 2.

2. Приведение контрпримера при опровержении некоторого утверждения. Для понимания и дальнейшего закрепления смысла изучаемого явления можно предложить студентам сформулировать обратное утверждение. Что получится? Как вы думаете, обратное утверждение является верным? Обоснуйте свою точку зрения.

3. Заполнение карточек, в которых приведено полное решение задачи, но фразы в условии, связанные с выведенными ранее законами, формулами, известными фактами, заменены символом  (таким образом произойдет обращение к уже имеющемуся опыту студентов). Для разрешения трудностей, возникающих при решении задачи, к карточке может быть предложен ряд уточняющих вопросов.

4. Самостоятельное составление студентами прикладных задач по некоторым заранее заданным элементам.

В процессе проведения занятий по математике с использованием прикладных задач (в основе которых находятся проблемы, связанные с работой предприятий горной промышленности, и пути их решения) нами было отмечено, что у студентов проявляется не только интерес к решению задач, но и осознание всей меры ответственности при принятии инженерных решений, а это в свою очередь активизирует учебную деятельность обучающихся.

Результаты исследования и их обсуждение

В проведении экспериментальной работы принимали участие студенты 1 и 2 курсов, обучающиеся по направлению подготовки 21.05.02 Прикладная геология и 21.05.04 Горное дело ФГБОУ ВО «Уральский государственный горный университет» (г. Екатеринбург). Экспериментальная группа – 90 чел., контрольная – 96 чел.

Для проверки эффективности методики обучения математике, использование которой обеспечит формирование критического мышления у студентов горных вузов, были выделены уровни сформированности критического мышления и дана их краткая характеристика.

Начальный уровень сформированности критического мышления предполагает, что студент совместно с преподавателем способен производить отбор и интерпретацию информации, выявлять проблему, активизировать необходимый для решения задачи собственный опыт.

Средний уровень сформированности обеспечивается умениями студента самостоятельно производить поиск недостающей (избыточной) информации, выдвигать гипотезы, аргументировать их, оспаривать чужие гипотезы; строить и анализировать математическую модель описанного в задаче явления, решать задачу, осуществлять проверку решения.

Высокий уровень достигается умениями студента самостоятельно оценивать адекватность построенной математической модели по введенным критериям, выявлять несоответствие (противоречие) построенной модели изучаемому процессу, формулировать выводы с качественным обоснованием, прогнозировать дальнейшее развитие изучаемого процесса, оценивать процесс решения с точки зрения его оптимальности.

В процессе формирующего этапа экспериментальной работы была проведена диагностика уровней сформированности критического мышления у студентов горных вузов, предполагающая три среза (по окончании первого, второго и третьего семестров).

Таблица 3

Разделение студентов по уровням сформированности критического мышления в конце эксперимента

Разделение студентов в контрольной и экспериментальной группах по уровням сформированности критического мышления в конце эксперимента представлено в табл. 3.

Для проверки достоверности итогов экспериментальной работы нами была выполнена статистическая обработка полученных результатов на основе критерия χ2 Пирсона для сопоставления двух эмпирических распределений по одному признаку.

Нами рассмотрены следующие гипотезы.

Н0 (нулевая гипотеза): распределение студентов экспериментальной группы по уровням сформированности критического мышления является случайным, разработанная методика не влияет на уровень сформированности критического мышления студентов.

Н1 (альтернативная гипотеза): распределение студентов в экспериментальной группе по уровням сформированности критического мышления обусловлено применением разработанной методики обучения математике.

Согласно критерию Пирсона были найдены значения 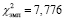и 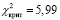. 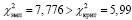, значит, принимается H1 (альтернативная гипотеза): распределение студентов в экспериментальной группе по уровням сформированности критического мышления обусловлено применением разработанной методики обучения математике.

Выводы

Полученные результаты дают нам основание сделать следующие выводы:

1) в ходе образовательного процесса необходимо помочь обучающимся научиться выявлять истинность или неистинность предлагаемой информации, но только через их самостоятельную деятельность;

2) для формирования критического мышления у студентов горных вузов необходимо разработать и внедрить в процесс обучения методическое обеспечение, содержащее в себе прикладные задачи, обеспечивающие междисциплинарные связи математики с профессионально-прикладными дисциплинами горного дела;

3) организовать процесс решения студентами задач необходимо на основе принципов: активного взаимодействия, творчества, опоры на субъектный опыт, управляемого перехода от деятельности в учебной ситуации к деятельности в профессиональной ситуации, предоставляя обучающимся возможность анализировать, оценивать, опровергать, выявлять противоречия, делать выводы, видеть применение полученных знаний в практической деятельности.