В настоящее время главной целью образования является формирование разносторонне развитой личности, широкого научного кругозора, общекультурных интересов и творческого потенциала ученика, способного самореализоваться во всех сферах деятельности. Для достижения данных целей особое внимание стало уделяться поисково-исследовательской деятельности обучающихся. На современном этапе обучения поисково-исследовательская деятельность учащихся рассматривается как инновационная образовательная технология, получившая широкое распространение в образовательном процессе. В соответствии с ФГОС ООО усвоение образовательной программы должно обеспечивать необходимость использования обучающимися поисково-исследовательской деятельности на основе регулятивных, познавательных, коммуникативных универсальных учебных действий, которые составляют основу поисково-исследовательской деятельности [1]. Данные аспекты справедливы для обучающихся школ, среднего профессионального звена и студентов вузов, в том числе педагогических.
Приобщение обучающихся к исследовательской деятельности в процессе обучения математике осуществляется с помощью особых исследовательских задач при изучении определённой методической линии.
Линия уравнений занимает важное место в курсе алгебры. Для изучения данной темы выделяется значительно больше часов, чем на какую-либо другую тему в школьном курсе математики. В содержании вузовского курса элементарной математики широко представлены виды уравнений и методы их решения. Это обусловлено тем, что уравнения являются эффективным средством закрепления, углубления и расширения теоретических знаний и развития творческой математической деятельности учащихся.
Анализ учебно-методической литературы, опыт педагогов-практиков позволяют сделать вывод о том, что проблеме организации поисково-исследовательской деятельности учащихся при решении уравнений в курсе алгебры не уделяется достаточного внимания. Методика обучения учащихся обычно выстраивается на основе использования традиционных методов и способов. Задачи исследовательского характера на занятиях рассматриваются и используются крайне редко.
Цель исследования – разработать и проверить экспериментально методические рекомендации по организации поисково-исследовательской деятельности студентов-математиков на примере обучения методам решения уравнений.
Материалы и методы исследования
Для изучения методических особенностей организации поисково-исследовательской деятельности студентов-математиков и экспериментальной проверки эффективности предлагаемой методики исследование проводилось на базе физико-математического факультета ФГБОУ ВО «Мордовский государственный педагогический университет имени М.Е. Евсевьева». В контексте исследования выполнен анализ научной и учебно-методической литературы. Наряду с теоретическими использовались и эмпирические методы исследования: наблюдение за процессом обучения студентов, работой преподавателей, а также их опросы. В исследовании использованы данные, полученные авторами в результате апробации разработанных методических рекомендаций в обучении студентов на учебных занятиях по математическим дисциплинам [2]. Описание теоретических основ поисково-исследовательской деятельности и выявление оптимальных условий ее организации в процессе обучения математике в высшей школе выполнено на основе деятельностного и технологического подходов [3].
Материалы статьи обладают практической значимостью для преподавателей методических дисциплин в контексте профессионально направленного обучения студентов педагогических вузов.
Результаты исследования и их обсуждение
В настоящее время образовательный процесс направлен на достижение таких серьёзных и значимых целей, как гармоничное развитие личности учащегося, формирование широкого научного кругозора, общекультурных интересов и общечеловеческих ценностей ученика. Одним из важнейших факторов, необходимых для достижения данных целей, является приобщение учащихся к познанию окружающей действительности, исследованию изучаемых процессов и явлений. В связи с этим под организацией исследовательской деятельности обучающихся понимается серьёзная инновационная образовательная технология, и, в свою очередь, проблема использования в образовательном процессе учебных исследований является актуальной и многоаспектной.
Включение учебных исследований в образовательный процесс, выделяя при этом существенные характеристики, определяющие основные направления и значимость использования учебных исследований, в свою очередь, подчёркивает важность организации и приобщения учащихся к поисково-исследовательской деятельности.
Понятие поисково-исследовательской деятельности неоднократно являлось объектом рассмотрения у разных авторов и авторских коллективов, каждый из которых выделял в определении данного понятия, по их мнению, наиболее важные содержательные элементы.
Осуществив анализ рассмотренных определений, можно заметить, что поисково-исследовательская деятельность рассматривается в контексте разных подходов, а именно учитываются такие содержательные элементы, как решение проблемных заданий, самостоятельность поиска знаний, овладение новыми знаниями, овладение умением работать с информацией и построение целостной картины исследуемого фрагмента действительности.
В контексте данного исследования под поисково-исследовательской деятельностью будем понимать активную, самостоятельную деятельность, направленную на решение проблемных ситуаций путём исследований и анализа различного учебного материала, в результате которых происходит овладение новыми знаниями, умениями и навыками. Для данной деятельности должны выполняться этапы, характерные для научного исследования.
Активизация поисково-исследовательской деятельности учащихся зависит от некоторых условий, к которым можно отнести такие, как:
– благоприятная атмосфера и дружеский настрой в ученическом коллективе;
– согласованное сочетание индивидуальной и коллективной форм обучения;
– наличие организованной структуры, для которой характерно дифференцирование учебного материала по степени сложности;
– ознакомление обучающихся с приемами организации познавательной деятельности;
– наличие стойкой учебно-познавательной мотивации к обучению и саморазвитию.
К основным принципам организации учебного процесса, направленным на развитие поисково-исследовательской деятельности учащихся, относятся:
– развитие интереса к изучаемому объекту;
– осуществление принципа индивидуализации в обучении;
– конструирование заданий творческого характера, требующих использования нестандартных методов решения;
– сочетание методов, в частности дидактически и методически обоснованных, которые направлены на развитие познавательной деятельности и творческих способностей учащихся.
Можно выделить следующие основные дидактические функции поисково-исследовательской деятельности:
1) открытие новых знаний (осуществляется работа непосредственно с понятием, выделением его существенных свойств и признаков; определения математических закономерностей и принципов; выбор наиболее рационального доказательства какого-либо утверждения и т.д.);
2) углубление полученных знаний (предполагает получение равносильных определений; обобщение уже изученных теорем, работа с доказательствами);
3) систематизация изученных знаний (функция направлена на установку связи между изученными понятиями и теоремами; структурирование и систематизацию учебного материала и т.д.);
4) развитие учащихся (функция направлена на переход учащихся из объекта обучения в субъект управления; а также формирование самостоятельности учащихся к самоуправлению);
5) обучение учащихся способам деятельности (предполагает обучение структуры учебного исследования, назначение её компонентов и основных этапов).
На основе анализа ряда исследований, проведенных разными авторами, в структуре учебного исследования можно выделить следующие этапы: постановка проблемы, выдвижение гипотезы, проверка гипотезы, вывод.
Этап постановки проблемы тесно связан с анализом и изучением задачной ситуации. В одних случаях с проблемы начинается учебное исследование, а в других проблема выступает как результат наблюдений за каким-либо объектом. На данном этапе необходимо поставить перед учащимся такое затруднение, преодоление которого активизировало бы его мыслительную деятельность; определить перед учащимся противоречия между возникшей познавательной потребностью и невозможностью удовлетворения данной потребности посредством имеющихся знаний, умений и навыков [4].
Составляя план решения поставленной проблемы, учащийся мысленно представляет результат решения данной проблемы, отмечая последовательность выполнения своих действий на основе имеющегося опыта и решения проблем. В результате этого возникает некоторая идея, на которой основано решение данной проблемы. Довольно часто только одно из нескольких предположений может являться гипотезой. Таким образом, гипотезой является только обоснованное предположение. Многие авторы считают, что для учебного исследования этап выдвижения гипотезы является очень важным и необходимым. Он возможен только при тщательном изучении фактов и явлений.
Следующим шагом после выдвижения гипотезы является проверка данной гипотезы. Проверка предполагает подтверждение, доказательство, обоснование или опровержение гипотезы. Обучающиеся должны уметь анализировать учебный материал, предложенный учителем, выделяя основные элементы, а также уметь сравнивать, синтезировать, сопоставлять, обобщать и делать необходимые выводы.
На основе определения главных и обязательных этапов исследования выделяются следующие ключевые приёмы организации поисково-исследовательской деятельности (таблица):
– постановка проблемы (обозначение тех вопросов, которые необходимо рассмотреть в ходе исследования);
– выдвижение гипотезы (высказывание определённых предположений, проведение рассуждений в ходе исследования);
– доказательство или опровержение гипотезы [5].
Приёмы организации поисково-исследовательской деятельности
|
Название приёма |
Действия, составляющие приём |
|
Приём постановки проблемы / приём представления проблемных заданий |
1. Осуществление анализа задачи, предполагающее выделение условия и требования представленной задачи. 2. Выполнение анализа возникшей проблемы. 3. Представление и формулировка проблемной задачи в виде вопроса или задания |
|
Приём выдвижения гипотезы / приём планирования возможных вариантов решения задачи |
1. Осуществление анализа возникшей проблемы. 2. Высказывание возможных предположений по решению данной проблемы. 3. Нахождение решения частных задач. 4. Синтез результатов, полученных при решении частных задач. 5. Формулировка гипотезы |
|
Приём доказательства гипотезы / приём выполнения плана и оценки результатов выполненной работы |
1. Определение того, какое из утверждений достаточно доказать для подтверждения гипотезы и осуществления его анализа. 2. Установление способа доказательства выбранного утверждения 3. Решение задачи на доказательство 4. Установление истинности или ложности полученных результатов. 5. Принятие или опровержение гипотезы |
Система упражнений, направленная на организацию поисково-исследовательской деятельности, должна содержать такие задачи, которые будут главным образом мотивировать учащихся на самостоятельный поиск необходимой информации; способствовать развитию умений анализировать, синтезировать и структурировать информацию, уметь преобразовывать её.
В соответствии с этим важно разработать систему заданий, которая способствует организации поисково-исследовательской деятельности учащихся. Выполнение данных заданий будет способствовать углублению и расширению имеющихся у учащихся знаний. Приведем пример учебного задания, выделив приемы поисково-исследовательской деятельности.
Задача 1. Найти значения параметра «а», при которых дробно-рациональное уравнение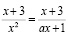 
имеет единственное решение.
Решение. Для решения данного уравнения воспользуемся аналитическим методом и составим следующую совокупность уравнений:
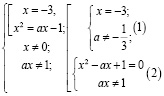
Рассмотрим несколько случаев.
1 случай.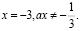 
Система (2) не должна иметь решений. Следовательно,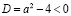 
или 
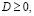но корни уравнения не удовлетворяют условию 
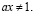Однако при 
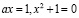уравнение не имеет решений. Получим: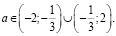
2 случай.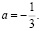 
Система (1) не имеет решений. Значит, система (2) примет вид:
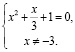
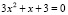– действительных корней нет.
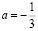не удовлетворяет условию, так как решений нет ни у одной из систем.
Ответ: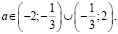 
При выполнении данного задания использовались следующие приёмы поисково-исследовательской деятельности:
– приём постановки проблемы (анализ условия задачи; определение вида уравнения; установление того, что необходимо найти);
– приём начального исследования проблемы и планирования возможных вариантов решения задачи (высказывание предположений по решению данных уравнений; актуализация понятия «параметр»; актуализация основных способов решения дробно-рациональных уравнений);
– приём выполнения плана и оценки результатов выполненной работы (непосредственное решение уравнений: для каждого из полученных значений параметра а определение корней дробно-рационального уравнения; установление конкретных значений параметра, при которых уравнение имеет единственное решение).
Для решения дробно-рациональных уравнений существует ещё один метод – метод неопределённых коэффициентов, который отличается простотой и удобством применения. Данный метод не включается в содержание школьных учебников алгебры. Он изучается в рамках вузовского курса элементарной математики. Данный метод рационален при решении сложных дробно-рациональных уравнений. Приведем пример такого учебного материала.
Задача 2. Решите уравнение:
.
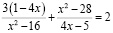Решение. Область допустимых значений: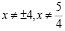 
.
Запишем исходное уравнение в виде
,
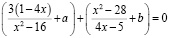где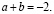 
Суть решения данного уравнения методом неопределённых коэффициентов заключается в следующем: необходимо подобрать такие значения a и b, чтобы в последующем числители дробей, которые входят в уравнение, были равны. Далее этот числитель, который является общим множителем, выносится за скобки, и решение уравнения сводится к решению двух уравнений:
,
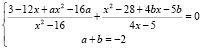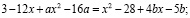
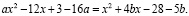
Получаем следующую систему:
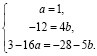
Из системы следует, что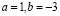 
, причём значения a и b удовлетворяют условию: 
.
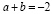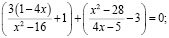
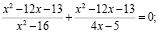
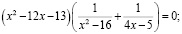
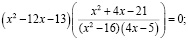
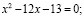или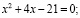 
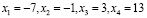∈ ОДЗ.
Ответ: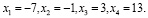 
При выполнении данного задания использовались следующие приёмы поисково-исследовательской деятельности:
– приём представления проблемного задания (анализ условия задачи; определение вида уравнения; знакомство учащихся с методом неопределённых коэффициентов при решении дробно-рациональных уравнений, определение его преимущества и значимости);
– приём планирования возможных вариантов решения задачи (высказывание предположений по решению уравнений c использованием изученного метода неопределённых коэффициентов);
– приём выполнения плана и оценки результатов выполненной работы (решение дробно-рациональных уравнений с использованием метода неопределённых коэффициентов).
Для закрепления умений и навыков учащихся в решении дробно-рациональных уравнений с параметром и решении дробно-рациональных уравнений с помощью метода неопределённых коэффициентов следует предложить аналогичные задания, которые могут быть представлены в качестве самостоятельной или домашней работы.
Заключение
В контексте данного исследования поисково-исследовательская деятельность определяется как активная, самостоятельная деятельность, направленная на решение проблемных ситуаций путём исследований и анализа различного учебного материала, в результате которых происходит овладение новыми знаниями, умениями и навыками.
Систематическая организация поисково-исследовательской деятельности студентов педагогического вуза по математическим дисциплинам обучающихся при решении уравнений, грамотно используя приёмы поисково-исследовательской деятельности, в значительной мере повысит эффективность и качество обучения учащихся.
Статья выполнена в рамках гранта на проведение научно-исследовательских работ по приоритетным направлениям научной деятельности вузов-партнеров по сетевому взаимодействию (Чувашский государственный педагогический университет имени И.Я. Яковлева и Мордовский государственный педагогический университет имени М.Е. Евсевьева) по теме «Формирование приемов поисково-исследовательской деятельности студентов педагогических вузов в процессе обучения математическим дисциплинам».