Проблема организации дорожного движения в городах является достаточно серьезной. Постоянно возникающие заторы на улично-дорожной сети ведут к снижению скорости движения, увеличению времени в пути, повышению расхода топлива, увеличению вредных выбросов в окружающую среду. Наиболее действенными мерами, способными обеспечить беззаторовое движение, являются расширение дорожной сети, строительство новых дорожных развязок, выведение транзитного транспорта за черту города. Однако в силу градостроительных особенностей это не всегда возможно. Поэтому оптимальная организация движения на уже существующей дорожной сети также является действенной мерой. Причем актуальной задачей является разработка методов автоматизированного принятия решений по организации движения в режиме реального времени.
В настоящее время существует большое количество математических моделей распределения транспортных потоков по сети и методов, способствующих решению задач оптимального управления ими [1–3]. Однако изучение методов моделирования и управления потоками остается актуальной задачей. Это связано с развитием технических возможностей сбора и обработки данных, а также с широким спектром задач, подлежащих исследованию.
Отдельной локальной задачей является организация движения на регулируемом пересечении. Исследования в этой области посвящены методам определения оптимальных фаз светофорного цикла и снижения очереди автотранспортных средств у перекрестка [4, 5]. Актуальной является задача разработки метода определения оптимальных параметров светофорного регулирования в режиме реального времени при минимальном количестве исходных данных, что и является целью данной работы.
Материалы и методы исследования
Для решения задач локального порядка, в частности организации движения на перекрестке со светофорным регулированием, необходимо разработать модель движения транспортных средств и выбрать критерий оптимизации. Критерий оптимизации будет определять направленность мероприятий по совершенствованию организации движения.
В данной работе перекресток рассматривается как узел транспортной сети, в котором пересекаются несколько транспортных потоков, распределенных по полосам движения. Каждый транспортный поток описывается как случайный поток событий, распределенный по закону Эрланга. Справедливость такой гипотезы была проверена автором экспериментально [6]. В качестве критерия оптимизации можно выбрать, например, среднюю часовую задержку на данном перекрестке (в автомобиле-часах); среднюю часовую задержку на данном перекрестке по выбранным приоритетным направлениям (в автомобиле-часах); среднюю задержку за один цикл [7]. Требованию минимизации общих транспортных расходов в сети (system optimization) отвечает критерий задача минимизации потерь времени на данном перекрестке всеми транспортными средствами.
Результаты исследования и их обсуждение
1. Модель регулируемого перекрестка
Автором разработана математическая модель движения автотранспортных средств по сети [6, 8] и выведены явные аналитические функции для определения параметров качества организации движения в случае, если справедлива гипотеза о распределении интервалов по времени между автомобилями по закону Эрланга. Явное аналитическое задание функции позволяет провести исследование на наличие ее экстремумов средствами математического анализа.
Пусть n1 – число потоков магистрали № 1; n2 – число потоков магистрали № 2;
h – среднее время (в секундах) между пересекающими узловую точку требованиями одного потока;
Hi(t, λ) – функция восстановления для i-го потока магистрали № 1;
Wi(Ti, λ) – суммарная задержка всех требований i-го потока за один цикл регулирования;
T1 – время (в секундах), в течение которого запрещено движение для потоков магистрали номер № 1:
T2 – время (в секундах), в течение которого запрещено движение для потоков магистрали номер № 2 :
Y – время (в секундах) горения желтого сигнала;
длина цикла светофорного регулирования:
T1 + T2 + Y = T. (1).
Под задержкой на перекрестке будем понимать время ожидания возможности продолжить движение в нужном направлении, вызванное запрещающим сигналом светофора. Суммарная задержка всех транспортных средств данного потока за единицу времени – один час – выражается следующим образом:
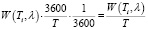(авт.∙ч). (2)
Целевая функция:
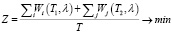. (3)
В результате следует получить оптимальные значения параметров регулирования T, T1, T2.
При этом для каждого потока должно выполняться условие отсутствия затора: при движении по данной полосе количество автомобилей, прибывающих к перекрестку за один цикл, не должно превышать количество требований, пересекающих этот перекресток за время Ti, когда движение разрешено. Ниже сформулированы условия отсутствия затора:
, 
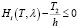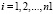; (4)
, 
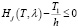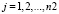. (5)
Кроме этого, необходимо выполнение условий:
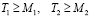, (6)
где M1, M2 – минимальная допустимая по нормативам длительность фаз светофорного цикла (в секундах).
В работе [6] экспериментально проверено, что значение параметра k распределения Эрланга может принимать значения от одного до четырех. Значения параметра λ зависят от интенсивности движения. Функции Hi(t, λ) и Wi(Ti, λ) в каждом случае следующие:
Параметр k = 1)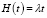 
; 
;
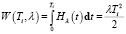Параметр k = 2)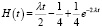 
;
;
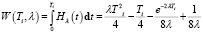Параметр k = 3)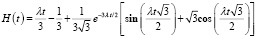 
;
;
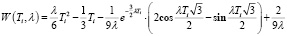параметр k = 4)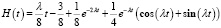 
;
.
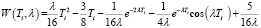2. Разработка алгоритма решения задачи
Для разработки алгоритма докажем следующее утверждение.
Теорема 1. Функция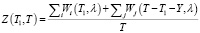 
не имеет критических точек в области определения.
Доказательство.
Критические точки являются решением системы:
Ω: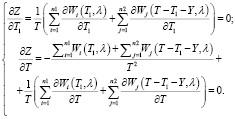 
C учетом того, что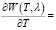 
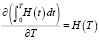, продолжим вычисление 
:
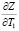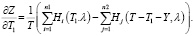
Найдем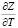 
:
.
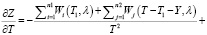
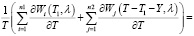
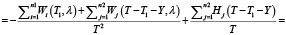
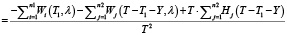Так как функция H(t) возрастает, то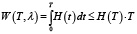 
. Можно оценить значение частной производной по Т.
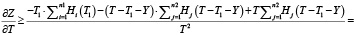
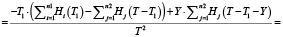
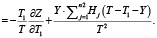
Если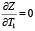 
, то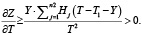 
Знак неравенства строгий, так как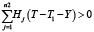 
(иначе движение в направлении 2 отсутствует).
Таким образом, функция Z(T1,T) не имеет критических точек.
Что и требовалось доказать.
Следствие: целевая функция
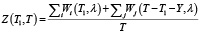
может достигать экстремума (в частном случае минимума) только на границе области определения:
.
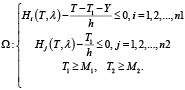Исходя из этого, возможно разработать алгоритм решения данной задачи математического программирования. Ниже отметим следующие факты, которые будут учтены при разработке алгоритма.
1. Пусть при T = T* и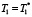 
целевая функция Z(T1,T) достигает наименьшего значения при выполнении условий Ω. Тогда хотя бы одно из неравенств системы ограничений обращается в равенство.
2. Система ограничений линейна относительно параметра T1, тогда
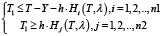
То есть множество допустимых значений Ω не пустое, если выполнено условие
.
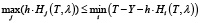Если
,
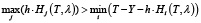то задача не имеет решений.
Алгоритм решения
Шаг 1) при T = Tmax проверяем выполнение условия:
.
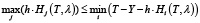Если выполнено, то переходим к шагу 2, если не выполнено – к шагу 3.
Шаг 2) находим наименьшее Z(T1,T) значение для T = Tmax
2.1) принимаем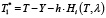 
для i = 1;
2.2) если T1* ≥ М1 и
,
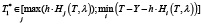то принимаем значение T1* за решение задачи. Вычисляем Z(T1*);
2.3) если не все условия выполнены, то переходим к пункту 2.4;
2.4) повторяем пункты 2.1–2.4 для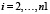 
;
2.5) принимаем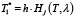 
для j = 1;
2.6) если T1* ≥М1 и
,
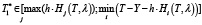то принимаем значение T1* за решение задачи. Вычисляем Z(T1*);
2.7) если не все условия выполнены, то переходим к пункту 5;
2.8) повторяем пункты 2.5 – 2.7 для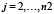 
;
2.9) из всех найденных Z(T1*) выбираем наименьшее значение.
Шаг 3) проверяем выполнение условия
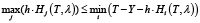
при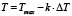 
, 
.
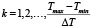Точность достаточно взять ΔТ = 1.
Если выполнено, то переходим к шагу 2, если не выполнено – изменяем значение Т.
Шаг 4) среди всех найденных значений Z(T1*) выбираем наименьшее, соответствующие значения параметров являются решением задачи.
Замечания:
1. Если ставится задача свести к минимуму суммарные затраты времени на регулируемом перекрестке в определенном направлении, то изменяется числитель целевой функции (суммируем затраты времени только в выбранном направлении). Например,
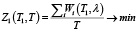
или
.
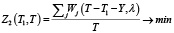Функция Z1(T1,T) оптимизирует суммарную часовую задержку в направлении № 1, а Z2(T1,T) – в направлении № 2. Обе функции монотонные по аргументу Т1, поэтому наименьшее значение достигается также на границе области Ω. Поэтому можно использовать предложенный выше алгоритм.
2. Если интенсивность движения в каком-либо направлении высокая и очередь из транспортных средств не успевает ликвидироваться за время горения разрешающего сигнала светофора, то соответствующее неравенство в системе Ω не может быть выполнено; в этом случае можно исключить его из рассмотрения и найти оптимальные фазы цикла для остальных направлений.
По алгоритму из пункта 2.2 автором разработан программный модуль среде DELPHI (рисунок).
Заключение
Предлагаемый метод определения параметров цикла светофорного регулирования приемлем для его корректировки в режиме реального времени, так как по заданным параметрам потоков мгновенно выдает решение. Кроме того, предлагаемый способ определения задержек на регулируемом перекрестке позволяет проводить предварительную оценку суммарных потерь времени при проектировании пересечения, определении числа полос и схемы движения на подходах к перекрестку.
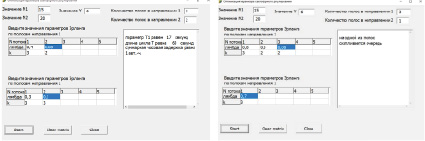
Пример работы программы, определяющей оптимальные параметры цикла светофорного регулирования