Конкурентоспособность предприятий легкой промышленности напрямую зависит от качества производимых ими изделий. В свою очередь, качество одежды определяется в том числе качеством материалов и их соответствием установленным требованиям. Задача эффективности выбора материалов для изготовления определенной продукции является многокритериальной, требующей определения комплексного показателя качества. Для решения многокритериальных задач используются различные методы построения обобщенного показателя [1–4], одним из которых является функция желательности Харрингтона. При этом для реализации математического функционала методов определения комплексного показателя качества, при учете максимально возможного числа частных показателей, необходимо использовать автоматизированные способы обработки данных с применением соответствующих программных средств.
Разработка технологии автоматизированного расчета комплексного показателя качества материалов для изготовления изделий легкой промышленности с использованием обобщенной функции желательности Харрингтона позволит оптимизировать процесс обоснованного выбора материалов исходя из заданных требований и условий эксплуатации проектируемой одежды.
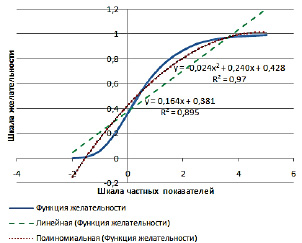
Рис. 1. График функции желательности Харрингтона
Цель работы – разработка инструментария на основе компьютерных технологий для комплексной оценки уровня качества материалов для одежды специального назначения.
Материалы и методы исследования
Комплексная оценка качества материалов, применяемых в производстве одежды специального назначения, в данной работе проводилась на основе построения обобщенной функции желательности Харрингтона. Стандартные оценки по шкале желательности приведены в табл. 1 [5]. Функция желательности может быть определена графическим или аналитическим методом. Разработка автоматизированных способов реализации аналитического метода на основе компьютерных технологий значительно снизит трудоемкость и повысит точность расчетов.
Функция желательности, соответствующая шкале желательности Харрингтона для одностороннего ограничения, имеет вид
di = exp( -exp(-y)) или 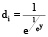 , (1)
, (1)
где y – кодированное значение частного параметра у.
Обобщенный показатель желательности (D) рассчитывается по формуле (2).
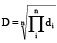 . (2)
. (2)
Перевести значения размерных (натуральных) показателей (х) качества изделий в безразмерные (у) можно по формулам [5, 6]:
– при линейной зависимости y = a0 + a1x, (3)
– при нелинейной связи y = a0 + a1x + a2x2. (4)
График функции желательности Харрингтона с односторонним ограничением представлен на рис. 1. В программной оболочке Excel с помощью трендового анализа были построены графические зависимости и найдены корреляционные уравнения связи между частными показателями и шкалой желательности [6], представленные на рис. 1.
Анализ величин достоверности аппроксимаций показал, что при параболическом полиноме (R2 = 0,97) погрешность аппроксимации меньше, чем при линейном тренде (R2 = 0,895). Потому для разработки комплексного показателя качества в данном исследовании был взят параболический тренд функции желательности.
Прологарифмировав дважды уравнение (1) с учетом результатов проведенной выше аппроксимации и соответственно уравнения (4), составляем систему уравнений для определения частных функций желательности:
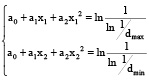 , (5)
, (5)
где dmax и dmin – значения шкалы желательности «отлично и «удовлетворительно»;
х1, х2 – значения исследуемых показателей, соответствующих оценкам шкалы желательности «отлично» и «удовлетворительно» соответственно.
Для комплексной оценки качества материалов в соответствии с выражениями (1–5) был разработан алгоритм, наглядно представленный на рис. 2 и позволяющий определять обобщенные показатели желательности для i-го числа тканей и n-го числа исследуемых свойств для каждой ткани.
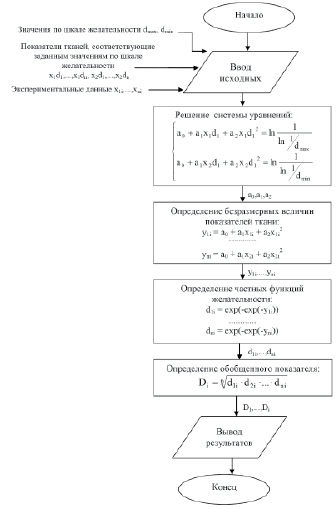
Рис. 2. Алгоритм комплексной оценки качества материалов
Таблица 1
Шкала оценок исследуемых показателей
|
Градация качества |
Оценки по шкале желательности |
xd1 |
xd2 |
xd3 |
xd4 |
xd5 |
xd6 |
xd7 |
xd8 |
|
Отлично |
1,00–0,80 |
1600 |
1000 |
60 |
60 |
1,5 |
1,2 |
25000 |
60 |
|
Хорошо |
0,79–0,64 |
1000 |
700 |
40 |
40 |
2 |
1,5 |
15000 |
40 |
|
Удовлетворительно |
0,63–0,37 |
500 |
400 |
30 |
30 |
2,4 |
1,7 |
5000 |
20 |
|
Плохо |
0,36–0,20 |
300 |
200 |
20 |
20 |
2,7 |
2 |
2000 |
10 |
|
Очень плохо |
0,19–0,00 |
200 |
150 |
10 |
10 |
3 |
2,3 |
1000 |
7 |
Таблица 2
Экспериментальные показатели материалов для спецодежды
|
Номер ткани |
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
х8 |
|
1 |
1500 |
900 |
55 |
52 |
1,8 |
1,3 |
20 000 |
55 |
|
2 |
1150 |
900 |
35 |
25 |
2 |
1,8 |
30 000 |
45 |
|
3 |
1200 |
900 |
55 |
40 |
2 |
1,4 |
28 000 |
30 |
|
4 |
2500 |
700 |
64 |
50 |
2 |
1,5 |
32 000 |
25 |
|
5 |
1500 |
600 |
30 |
20 |
2 |
1,8 |
15 000 |
40 |
|
6 |
1300 |
850 |
50 |
45 |
1,9 |
1,2 |
15 000 |
80 |
|
7 |
1300 |
1000 |
64 |
55 |
2 |
1,4 |
35 000 |
40 |
|
8 |
1000 |
1200 |
55 |
60 |
1,7 |
1,2 |
35 000 |
30 |
|
9 |
1600 |
800 |
55 |
25 |
2 |
1,9 |
35 000 |
50 |
|
10 |
2500 |
900 |
64 |
60 |
2 |
1,4 |
30 000 |
80 |
|
11 |
1700 |
600 |
64 |
25 |
2 |
1,5 |
20 000 |
60 |
|
12 |
1000 |
700 |
50 |
45 |
2 |
1,4 |
15 000 |
60 |
Для определения комплексного показателя качества тканей, применяемых для производства одежды специального назначения, были выбраны: х1 – разрывная нагрузка по основе,(N); х2 – разрывная нагрузка по утку,(N); х3 – раздирающая нагрузка по основе (N); х4 – раздирающая нагрузка по утку (N); х5 – усадка по основе (%); х6 – усадка по утку (%); х7 – число циклов истирания, х8 – воздухопроницаемость (дм³/(м²·с)).
На основе анализа требований к материалам для спецодежды [7, 8] были установлены значения вышеуказанных показателей тканей (xd1,...,xdn), соответствующие градации качества по шкале желательности, и представлены в табл. 1.
В качестве dmax и dmin были приняты значения нижней границы зоны «отлично» и «удовлетворительно»: dmax = 0,8; dmin = 0,37
В рамках исследования для испытаний были взяты 12 образцов тканей для спецодежды. Экспериментальным путем определены значения показателей х1–х8 представленные в табл. 2.
Программная реализация предложенного алгоритма осуществлялась в математическом редакторе Matchcad. Фрагмент решения системы уравнений (5) представлен на рис. 3.
С использованием данной программы была проведена комплексная оценка качества на основе функции желательности Харрингтона для всех исследуемых образцов тканей для одежды специального назначения.
Результаты исследования и их обсуждение
В результате решения системы уравнений (5) были получены математические модели взаимосвязи натуральных показателей и их безразмерных величин:
y1 = -8,27∙10-4∙x+1,677∙10-6∙x2
y2 = -1,956∙10-3∙x+4,926∙10-6∙x2
y3 = -0,049∙x+1,644∙10-3∙x2
y4 = -0,035∙x+1,408∙10-3∙x2
y5 = 4,87-0,845∙x2
y6 = 5,914-2,044∙x2
y7 = -2,826∙10-5∙x+5,883∙10-9∙x2
y8 = -0,024∙x+2,456∙10-3∙x2
В результате автоматизированного расчета в программе Matchcad были получены значения частных и комплексного показателя качества для исследуемых образцов материалов, представленные в табл. 3. Применение разработанной программы автоматизированного определения функции желательности Харрингтона предусматривает графическую интерпретацию результатов. На рисунке 4 представлен график полученных комплексных показателей для исследуемых образцов тканей.
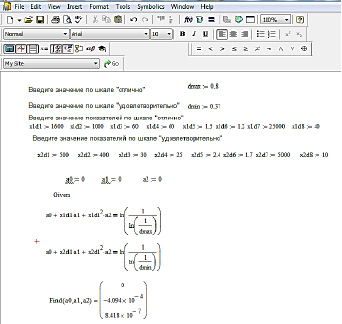
Рис. 3. Фрагмент программной реализации комплексной оценки качества материалов
Таблица 3
Результаты аналитической оценки функции желательности Харрингтона
|
Номер образцов тканей |
Частные желательности |
Обобщенная желательность |
|||||||
|
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
d7 |
d8 |
D |
|
|
1 |
0,924 |
0,898 |
0,903 |
0,872 |
0,888 |
0,918 |
0,846 |
0,998 |
0,905 |
|
2 |
0,754 |
0,898 |
0,476 |
0,37 |
0,798 |
0,37 |
0,988 |
0,98 |
0,576 |
|
3 |
0,786 |
0,898 |
0,903 |
0,653 |
0,798 |
0,862 |
0,978 |
0,798 |
0,829 |
|
4 |
0,999 |
0,703 |
0,973 |
0,843 |
0,798 |
0,765 |
0,994 |
0,675 |
0,835 |
|
5 |
0,924 |
0,578 |
0,371 |
0,318 |
0,798 |
0,131 |
0,666 |
0,95 |
0,504 |
|
6 |
0,842 |
0,861 |
0,827 |
0,756 |
0,85 |
0,95 |
0,666 |
0,999 |
0,838 |
|
7 |
0,842 |
0,95 |
0,973 |
0,908 |
0,798 |
0,862 |
0,998 |
0,95 |
0,908 |
|
8 |
0,652 |
0,991 |
0,903 |
0,95 |
0,916 |
0,95 |
0,998 |
0,798 |
0,887 |
|
9 |
0,95 |
0,815 |
0,903 |
0,37 |
0,798 |
0,013 |
0,998 |
0,993 |
0,477 |
|
10 |
0,999 |
0,898 |
0,973 |
0,95 |
0,798 |
0,862 |
0,988 |
0,999 |
0,931 |
|
11 |
0,968 |
0,578 |
0,973 |
0,37 |
0,798 |
0,765 |
0,846 |
0,999 |
0,753 |
|
12 |
0,652 |
0,703 |
0,827 |
0,756 |
0,798 |
0.862 |
0,667 |
0,999 |
0,776 |
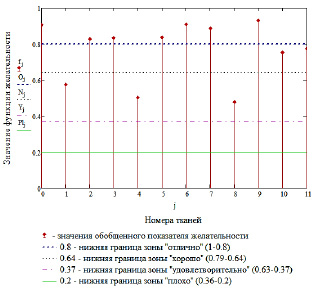
Рис. 4. Графическая оценка обобщенной функции желательности Харрингтона
Использование графического представления результатов исследования позволяет наглядно оценить, в какую зону шкалы желательности попадает обобщенный показатель материала и, соответственно, уровень качества исследуемого изделия. Поскольку к одежде специального назначения предъявляются довольно строгие требования ввиду особенностей ее эксплуатации, поэтому приемлемый уровень качества установим по нижней границе зоны «хорошо», то есть 0,64. Материалы, которые имеют значение комплексного показателя менее 0,64, не могут использоваться для производства спецодежды.
Заключение
Анализ результатов исследования, представленный в табл. 3 и на рис. 4, показал, что ткани № 2, 5, 9 имеют неприемлемый уровень качества (обобщенный показатель < 0,64). Остальные образцы исследуемых материалов имеют значения обобщенной функции по шкале «отлично» и «хорошо», и их можно рекомендовать для проектирования одежды специального назначения.
Таким образом, в работе предложен подход многокритериальной оценки качества изделий на основе обобщенной функции желательности Харрингтона с применением компьютерных технологий, практическое применение которого позволит автоматизировать и значительно ускорить оценку соответствия тканей предъявляемым требованиям.



