Применение бронхопластики направлено на удаление части крупного бронха с очагом поражения и последующей его пластикой. При этом чаще всего хирург сталкивается с проблемой различных диаметров бронхов при их сшивании, это обусловлено сложной внутренней структурой легочных образований, и врач интуитивно производит подобный вид операций, опираясь на основные хирургические принципы [1] и по-своему оценивая и реализовывая натяжение анастомозируемых бронхов, упуская при этом факторы возникающей деформации, посредством которых происходят изменения размеров и форм частей бронхиального дерева, а также возникающие при этом силовые напряжения между отдельными частями легких (рис. 1).
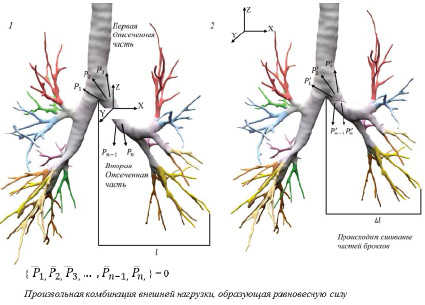
Рис. 1. Бронхиальное дерево с учетом внутренних усилий и их распределением по сечению: 1) до наложения анастомоза; 2) после наложения анастомоза с учетом изменения размеров бронхиального дерева
Следует отметить, что отсутствие учета этих факторов может привести к нарушению прочности бронхиального анастомоза в послеоперационном периоде, т.к. при чрезмерном натяжении бронх начинает испытывать сильные внутренние напряжения, что увеличивает вероятность несостоятельности шва. Так, согласно литературным источникам, частота нарушения целостности бронхиального шва в послеоперационный период составляет до 35% [2].
Для описания эффектов, возникающих в результате деформаций, связанных с неоднородностью бронхиального дерева, т.е. когда в результате заболевания меняются некоторые части бронхов, предлагается модель переменного коэффициента жесткости бронхиального дерева, задача которой заключается в определении интенсивности внутренних сил по сечению, что будет позволять контролировать изменения формы и размеров бронхиального дерева в результате напряжений, вызванных приложенными нагрузками с учетом сил, действующих между отдельными частями легких, зависящих от деформации во избежание полного нарушения прочности бронхиального дерева.
Следовательно, при создании модели переменного коэффициента жесткости бронхиального дерева следует:
− учитывать деформацию на выделенном участке сечения планируемой резекции бронхиального дерева с постоянном напряжением;
− контролировать изменения формы или размеров бронхиального дерева на этом участке при фиксированной деформации;
− определять соотношение, характеризующее изменения некоторых частей бронхиального дерева, возникающих в результате деформаций.
Цель исследования – выбор наилучших аналогов, используемых для исследования напряженно-деформированного состояния при создании модели переменного коэффициента жесткости бронхиального дерева, учитывающей предел прочности анастомоза.
Отметим, что входной информацией данной модели являются снимки КТ с автоматическим выделением границ и структуры патологии [3].
Для достижения поставленной цели необходимо решить следующие задачи:
− провести обзор моделей, используемых для исследования напряженно-деформированного состояния;
− выделить их преимущества и недостатки;
− выбрать наилучший вариант для реализации модели переменного коэффициента жесткости бронхиального дерева.
Материалы и методы исследования
Успех выполнения бронхопластики зависит от правильно созданного анастомоза между резецированными частями бронхов, который прежде всего должен быть прочным, а прочностный анализ позволяет проводить существующие модели напряженно-деформированного состояния.
Оценка напряженно-деформированного состояния по сечению ставит своей задачей определение внутренних напряжений, деформаций и перемещений в различных точках деформируемого тела произвольных размеров [4], возникающих под действием внешних нагрузок.
В связи с этим будут рассмотрены пять механических моделей напряженно-деформированного состояния для выявления наилучшей при создании модели переменного коэффициента жесткости.
Модели напряженно-деформированного состояния
Отметим, что свойства бронхиального дерева представляют сочетание вязкостных и эластичных характеристик, при этом зависящих от времени возникающего напряжения под действием деформации. Также бронх имеет сложную внутреннюю неоднородную структуру, состоящую из дискретных частей, в силу которых механические свойства материала различны по направлениям.
Модель типа Максвелла [5] является простой двухпараметрической моделью, описывающей поведение упругого элемента Е, осложненного вязкостью элемента η (рис. 2). Так, результатом работы [6] является анализ свойств данной модели, описание которых затрагивает лишь некоторые основные особенности поведения материалов при возникающей деформации.
Модель типа Фойгта [5] в свою очередь также состоит из двух составляющих, но уже параллельно соединенных вязкого η и упругого Е элементов (рис. 3). Так, в работе [7] данная модель не дает верного описания поведения материала под нагрузкой.
Модель типа Кельвина [5] состоит из последовательного соединения модели типа Фойгта и упругого Е1 элемента, что не допускает мгновенной деформации, при этом учитывает вязкие явления ползучести и релаксации (рис. 4). Однако описание ползучести данной модели начинается при любой приложенной нагрузке, какой бы небольшой она ни была, что не всегда имеет место для реальных вязких твердых тел: эта модель не включает пороговый эффект. Кроме того, это придает ему характер обратимости: снятие напряжений вызывает полное возвращение твердого тела к его исходному состоянию без ограничений и остаточных деформаций. По этой причине твердое тело Кельвина-Фойгта является вязкоупругим.
Модель типа Бюргерса [5] состоит из двух упругих элементов и двух элементов вязкости, соединенных как комбинация последовательно расположенных отдельных элементов, или из последовательного соединения модели типа Максвелла и модели типа Фойгта (рис. 5). Данная модель описывает восстановление после ползучести.
Модель типа Бранкова, или пятипараметрическая модель [5], состоит из четырехэлементной модели типа Бюргерса с последовательно связанной моделью типа Максвелла и моделью типа Кельвина (рис. 6). Так, в работе [8] показано, что данная модель описывает все стадии ползучести, но допускает погрешности, касающиеся описания начальной скорости и скорости ползучести, возрастающей до разрушения.
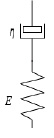
Рис. 2. Модель типа Максвелла
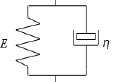
Рис. 3. Модель типа Фойгта
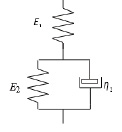
Рис. 4. Модель типа Кельвина
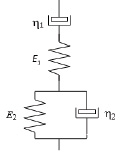
Рис. 5. Модель типа Бюргерса
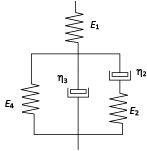
Рис. 6. Модель типа Бранкова
Критерии оценки моделей напряженно-деформированного состояния
Оценка моделей напряженно-деформированного состояния по сечению проводилась по следующим критериям:
a) удлинение с постоянной нагрузкой и последующей фиксацией деформации

b) удлинение с постоянной нагрузкой с последующим изменением относительно растяжения

c) простота моделей

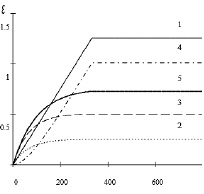
Рис. 7. Удлинение при постоянной нагрузке с последующей фиксацией деформации: 1) модель типа Максвелла, 2) модель типа Фойгта, 3) модель типа Кельвина, 4) модель типа Бюргерса, 5) модель типа Бранкова [9]
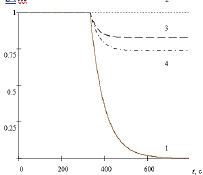
Рис. 8. Удлинение с постоянной нагрузкой с последующим изменением относительно растяжения: 1) модель типа Максвелла, 2) модель типа Фойгта, 3) модель типа Кельвина, 4) модель типа Бранкова [9]
Оценка моделей напряженно-деформированного состояния по выявленным критериям
|
Аналоги |
Оценка по критериям, балл |
∑, балл |
||
|
a |
b |
c |
||
|
Модель типа Максвелла |
0,5 |
0,5 |
1 |
2 |
|
Модель типа Фойгта |
1 |
0 |
1 |
2 |
|
Модель типа Кельвина |
1 |
1 |
0,5 |
2,5 |
|
Модель типа Бюргерса |
0,5 |
0,5 |
0 |
1 |
|
Модель типа Бранкова |
1 |
0,5 |
0 |
1,5 |
Согласно полученным графическим изображениям зависимостей деформации и релаксации от времени растяжения (рис. 7, 8 соответственно) при постоянной нагрузке модели типов Бюргерса и Максвелла описывают практически изменение только одного линейного размера бронха, причем с одним и тем же углом наклона (рис. 7), но в начальный момент времени их поведение различно: модель типа Бюргерса описывает нагрузку пропорционально значению самой величины действия удлинения, а модель типа Максвелла – строго линейную зависимость. В моделях типов Кельвина, Фойгта и Бранкова нарастание деформации происходит по экспоненциальным законам, однако при фиксации деформации модель типа Фойгта не описывает релаксацию напряжения, а модели типов Кельвина и Бранкова описывают достаточно сильное изменение относительно удлинения [9].
Нелинейная модель типа Максвелла вполне может описывать изменения реального бронха при растяжении, но графическая зависимость данной модели полностью релаксирует, что не может происходить с бронхом ввиду того, что в составе бронхиального дерева имеется коллаген и эластин. Подобное поведение описывают графические зависимости моделей типов Кельвина и Бранкова. Также обе эти модели имеют ограниченную релаксацию, как и бронхиальное дерево, однако определение всех параметров пятипараметрической модели типа Бранкова является достаточно сложной задачей [9].
Из проведенного аналитического анализа моделей сделан вывод, что наиболее адекватно поведение бронхиального анастомоза описывает модель типа Кельвина [9].
Результаты исследования и их обсуждения
Анализируя полученные результаты таблицы, выявили, что каждый из аналогов, наряду с преимуществами, обладает и недостатками, при этом нет ни одного аналога, который решал бы поставленную проблему. Поэтому в ходе исследования был выбран наилучший аналог для реализации модели переменного коэффициента жесткости бронхиального дерева, который описывает достаточно хорошо деформацию под действием внешних сил и при этом имеет ограниченную релаксацию, что в свою очередь наблюдается во время натяжения и после фиксации бронхиального шва.
Выводы
1. В ходе исследования был проведен обзор моделей, используемых для исследования напряженно-деформированного состояния.
2. Были выявлены их преимущества и недостатки.
3. Выбран наилучший аналог для реализации модели переменного коэффициента жесткости бронхиального дерева, которая в свою очередь направлена на помощь хирургу в предоперационной подготовке для описания эффектов, возникающих в результате деформаций, связанных с изменениями некоторых частей бронхиального дерева посредством хирургических вмешательств.



