Проблема моделирования связи между структурой и свойствами химических соединений – это важнейшая математическая задача современной теоретической и компьютерной химии [1-3]. Основная цель построения моделей связи «структура – свойство» – прогнозирование свойств химических соединений непосредственно по их структуре, при помощи соответствующих расчетов, минуя эксперимент. Результаты таких расчетов могут быть использованы для целенаправленного поиска соединений с заданными свойствами. Для моделей связи «структура – свойство», имеющих вид корреляционных уравнений, в литературе часто используется аббревиатура QSPR/QSAR (Quantitative Structure-Property/Activity Relationships), в зависимости от того, какое свойство соединений рассматривается: физико-химическое или какой-либо вид биологической активности.
Следует отметить, что экспериментальное определение различных свойств соединений с целью поиска соединений с заданным набором свойств во многих случаях является технически сложным и, кроме того, требует определенных финансовых и временных затрат. В связи с этим разработка, обоснование и тестирование различных математических методов моделирования связи между структурой и свойствами химических соединений является актуальной задачей.
Одним из наиболее распространенных подходов к моделированию связи «структура – свойство», приводящим к моделям, имеющим вид корреляционных уравнений, является так называемый статистический подход. Он заключается в следующем. Имеется набор химических структур {Si} (структурных формул молекул) с известными значениями {yi} некоторого свойства (физико-химического или биологической активности), i = 1, …, N. Требуется, анализируя эти данные, выявить зависимость свойства y от структуры S, т.е. найти функцию вида y = f(S), определяющую модель связи «структура – свойство».
Как правило, в этих исследованиях для описания структуры молекул используются взвешенные молекулярные графы (МГ), которые строятся по структурным формулам соответствующих молекул. Вершины этих графов соответствуют атомам молекулы (возможно, группе атомов), а ребра – химическим связям между ними. Числовые веса вершин и ребер кодируют атомы и связи различных типов; кроме того, могут быть приписаны некоторые веса и парам не связанных вершин графа. МГ задается своей матрицей весов. Следует отметить, что по первоначально определенной матрице весов МГ можно также построить много других матриц, модифицируя определенным образом элементы этой исходной матрицы.
Для количественной характеристики структуры молекул используются инварианты x1, …, xn соответствующего МГ (т.е. числа, вычисляемые по графу или его матрице, не зависящие от способа нумерации его вершин). В этом случае модель связи «структура – свойство» приобретает вид уравнения: y = f(x1, …, xn).
Таким образом, каждой исходной химической структуре S ставится в соответствие по некоторому правилу граф (или его матрица М), а этому графу, в свою очередь, сопоставляется некоторый набор инвариантов x1, …, xn, вычисляемых по определенным алгоритмам.
Далее предполагается, что функция многих переменных f(x1, …, xn) в уравнении связи «структура – свойство» имеет специальный вид (например, она является линейной или квадратичной), но зависит от ряда подгоночных параметров. Эти параметры определяются по исходным данным так, чтобы получаемое уравнение было бы как можно более точным на исходном наборе химических соединений.
Следует отметить, что при моделировании связи «структура – свойство» возникают проблемы выбора способа построения МГ, инвариантов МГ, а также аппроксимирующей функции f из бесконечного множества возможных вариантов. Однако этот выбор очень важен, так как от него зависит конечный результат моделирования.
Точность построенной модели можно оценивать разными способами (см., например, [4]). Например, можно использовать для этой цели такие статистические параметры соответствующего регрессионного уравнения, как коэффициент корреляции (R) и среднеквадратичное отклонение (s), максимальная и средняя относительные ошибки (δмакс и δср) расчета свойств исходной выборки (в %) при помощи полученного уравнения и т.д. При этом необходимо задать пороговые значения этих параметров, на основе которых модель будет признана «приемлемой» или нет. Эти пороговые значения зависят от конкретной задачи. Например, для физико-химических свойств обычно считается, что модель «хорошая», если R ≥ 0,95 или если δмакс ≤ 5%. Например, в [5] предложены следующие характеристики качества модели по величине коэффициента корреляции: R ≥ 0,990 (outstanding), R ≥ 0,975 (excellent), R ≥ 0,950 (very good), R ≥ 0,925 (good), R ≥ 0,900 (fair).
Одним из важных видов инвариантов графов являются инварианты спектрального типа, т.е. построенные на основе каких-либо спектральных характеристик матрицы графа [6; 7]. Основными спектральными характеристиками графа с n вершинами являются его собственные числа λ1 ≤ … ≤ λn (или коэффициенты характеристического полинома, которые выражаются через собственные числа), а также соответствующие собственные векторы.
Собственные числа графа несут в себе довольно большую информацию о структуре графа. Одно время даже считалось, что простой граф однозначно определяется по набору собственных чисел его матрицы смежности, но потом были найдены примеры, показывающие, что это не так. Как известно, матрица графа (как и любая матрица) однозначно восстанавливается по набору ее собственных чисел и соответствующих собственных векторов.
Инварианты спектрального типа широко используются в теории электронного строения сопряженных молекул. Примерами таких параметров являются: сумма положительных собственных чисел или их число, наименьшее положительное и наибольшее отрицательное собственное число и т.д. [6]. Кроме того, отдельные спектральные инварианты находят применение и в корреляциях «структура – свойство», совместно с молекулярными параметрами других видов [7; 8].
Цель исследования – построить и проанализировать регрессионные модели связи «структура – свойство» для разнообразных физико-химических свойств алканов, в которых используются инварианты МГ, основанные исключительно на собственных числах различных матриц этих МГ.
Исходные данные для построения корреляций
В качестве исходных данных для построения моделей связи «структура – свойство» была рассмотрена выборка структурных формул алканов с числом атомов углерода от 6 до 8 (всего N = 32 соединения), с известными значениями следующих физико-химических свойств: 1) температура кипения (bp – boiling point); 2) молярный объем (MV – molar volume at 20 °C); 3) молярная рефракция (MR – molar refraction at 20 °C); 4) теплота парообразования (HV – heat of vaporization at 25 °C); 5) критическая температура (TC – critical temperature); 6) критическое давление (PC – critical pressure); 7) поверхностное натяжение (ST – surface tension at 20 °C) [9].
Способы представления химических структур
Первоначально были построены простые МГ углеродных остовов алканов. Вершины этих МГ соответствуют атомам углерода, а ребра – химическим связям между ними. Затем для таких МГ были построены следующие простейшие матрицы: М1 = А (матрица смежности), М2 = D (матрица расстояний), М3 = V – М1 (матрица Кирхгофа), М4 = V+М2. Здесь V – матрица, диагональные элементы которой равны степеням соответствующих вершин МГ, а остальные элементы равны нулю. На рисунке приведен пример простого МГ углеродного остова 2-метилпропана и его матриц М1 – М4.
Заметим, что рассмотрение разных матриц одного простого МГ равносильно построению разных МГ, с разными весами вершин, ребер и пар несвязанных вершин.
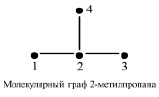
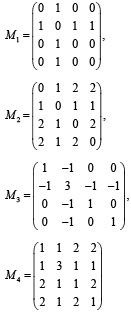
Простой молекулярный граф 2-метилпропана и его матрицы М1-М4
Инварианты, используемые для построения моделей связи «структура – свойство»
Пусть n – число вершин МГ, λ1 ≤ … ≤ λn – собственные числа какой-либо матрицы этого МГ (в данном случае – М1-М4). В работе рассматривались следующие инварианты спектрального типа, построенные при помощи некоторых простейших симметричных функций многих переменных и вычисленные для каждой из матриц М1-М4:
x1 = f1 (λ1, …, λn) = max λi;
x2 = f2 (λ1, …, λn) = min λi;
x3 = f3 (λ1, …, λn) = ∑|λi |2;
x4 = f4 (λ1, …, λn) = ∑|λi |3;
x5 = f5 (λ1, …, λn) = ∑ λi , λi >0;
x6 = f6 (λ1, …, λn) = ∑ (1 / λi ), λi >0;
x7 = f7 (λ1, …, λn) = (1 / n) × ∑ e λi ;
x8 = f8 (λ1, …, λn) = ∏ λi .
Отметим, что выбор этих симметричных функций был достаточно формальным и произвольным; он никак не связан ни с рассматриваемыми свойствами, ни с классом химических соединений. Кроме x1-x8, был рассмотрен также параметр x9 = n.
Следует подчеркнуть, что существует бесконечно много инвариантов МГ, которые могут использоваться в моделях связи «структура – свойство», и эти инварианты могут быть разных типов (см., например, [6]). Заранее неизвестно, от каких именно инвариантов и каким образом зависит изучаемое свойство для данного класса соединений. В связи с этим возникает проблема выбора конечного числа инвариантов МГ из бесконечного числа возможных вариантов. В нашей работе мы рассматриваем инварианты только одного типа – спектрального, что позволяет уменьшить степень неопределенности при выборе молекулярных параметров и алгоритмизировать процесс построения моделей.
Алгоритм построения корреляций «структура – свойство»
Для всех семи физико-химических свойств и отдельно для каждой матрицы М1-М4 были построены как линейные, так и нелинейные корреляции специального вида. Опишем в общем виде алгоритм, использованный нами для этих целей.
Пусть имеется выборка, состоящая из N химических структур с известными численными значениями yi (i=1,…,N) их некоторого свойства у (физико-химического или биологической активности) и известными численными значениями каких-либо их m структурных параметров x1,x2,…,хm. Задача заключается в построении корреляционного уравнения вида y=f(x1,x2,…,хm) (где функция f – это некоторый многочлен от переменных x1,x2,…,хm), удовлетворяющего определенным заданным требованиям. При этом, возможно, некоторые переменные из набора x1,x2,…,хm не будут входить в это уравнение; степень многочлена f может быть произвольной. Очевидно, что получаемое уравнение является линейным относительно выражений, являющихся произведением исходных переменных, взятых в некоторых целочисленных неотрицательных степенях, и поэтому оно определяет линейную регрессию, соответствующую исходной нелинейной регрессии.
Шаг 1. Назовем набор параметров x1,x2,…,хm исходным набором. Выберем некоторое число k (1≤k≤m). Из исходного набора параметров методом пошаговой линейной регрессии отберем k параметров xi1,…,xik, дающих наилучшую линейную корреляцию для свойства у (т.е. с наибольшим коэффициентом корреляции), и построим ее.
Параметры xi1,…,xik , вошедшие в полученную корреляцию, назовем базовыми.
Если качество полученной модели устраивает исследователя, то работа алгоритма на этом заканчивается. Если необходимо построить более точную модель, то переходим к Шагу 2.
Шаг 2. Образуем новое множество параметров, состоящее из базовых параметров (см. Шаг 1), их квадратов и всевозможных попарных произведений. Очевидно, что общее число параметров в новом множестве будет равно m1=k+0.5(k2+k)=0.5k2+1,5k.
Шаг 3. Идем на Шаг 1 и выполняем все действия, указанные в этом пункте, взяв в качестве исходного набора параметров новое множество параметров, сформированное на Шаге 2. Теперь в качестве m используется m1.
Результатом работы алгоритма являются регрессионные уравнения, полученные на Шаге 1, с такими их статистическими характеристиками, как коэффициент корреляции, среднеквадратичное отклонение, максимальная абсолютная ошибка расчетов свойств химических соединений исходной выборки по построенному уравнению (с указанием той структуры, на которой она реализуется), средняя относительная ошибка (в %). Кроме того, для каждой структуры заданной выборки приводятся расчетное значение свойства у, а также соответствующие абсолютная и относительная ошибки.
Отметим, что результат работы алгоритма (т.е. получаемая модель) существенно зависит от последовательности чисел k, выбираемых на Шаге 1 (при многократном повторении Шага 1). В связи с этим для получения лучшего результата или разных результатов целесообразно поварьировать цепочку чисел k. Из получаемых различных моделей можно выбрать одну или несколько наилучших (по какому-либо критерию). Таким образом, процедура построения моделей носит итерационный характер и в определенной степени управляется исследователем.
Таблица 1
Коэффициенты корреляции R нелинейных моделей для матриц М1-М4
|
Физ.-хим. св-во Матрица |
bp |
MV |
MR |
HV |
TC |
PC |
ST |
|
M1 |
0,9907 |
0,9963 |
0,9998 |
0,9914 |
0,9835 |
0,9355 |
0,9724 |
|
M2 |
0,9855 |
0,9930 |
0,9997 |
0,9790 |
0,9588 |
0,9105 |
0,9291 |
|
M3 |
0,9857 |
0,9940 |
0,9998 |
0,9896 |
0,9710 |
0,9397 |
0,9424 |
|
M4 |
0,9888 |
0,9955 |
0,9998 |
0,9888 |
0,9438 |
0,9105 |
0,8435 |
Вышеописанный алгоритм реализован нами в виде компьютерной программы на языке Java; при этом пользователь на первом этапе работы программы может выбрать некоторое подмножество множества параметров x1,x2,…,хm, с которым будет работать дальше.
При построении корреляций в настоящей работе в соответствии с описанным выше алгоритмом в качестве исходного набора использовались параметры x1-x9 (m=9), на Шаге 1 первоначально было выбрано k=3, на Шаге 2 новое множество параметров состояло из m1=9 параметров, при повторном выполнении Шага 1 было выбрано k=3. На этом процесс построения моделей заканчивался. Заметим, что похожая методика построения нелинейных корреляций использовалась нами ранее в работе [10].
Определение матрицы, дающей наилучшую модель
Далее была поставлена задача выбора одной матрицы графа из нескольких рассмотренных выше матриц, позволяющих получить наилучшую модель (как линейную, так и нелинейную). Наилучшей мы считаем модель с наибольшей величиной коэффициента корреляции R. При совпадении коэффициентов корреляции наилучшей считаем модель с наименьшим значением среднеквадратичного отклонения s. Соответствующую матрицу также назовем наилучшей.
В таблице 1 приведены значения коэффициентов корреляции (с четырьмя знаками после запятой) для нелинейных моделей для всех семи физико-химических свойств и всех матриц М1-М4. Такая точность в определении R необходима для максимальной дифференциации построенных моделей и выбора только одного варианта из нескольких возможных. При округлении R до трех знаков после запятой в ряде случаев различия между моделями по этому критерию исчезают.
На основе таблицы 1 можно сделать следующие выводы.
1. Наилучшую модель дает матрица М1 (для свойств bp, MV, HV, TC, ST).
2. Для свойства MR матрицы М1, М3, М4 дают одинаковый результат, но если учитывать s, то наилучшая – это М4.
3. Наилучший результат для свойства РС дает М3 (R = 0,9355). Однако в линейной корреляции наилучший результат дает М1 (R = 0,9413). Отметим, что, используя матрицу М1, в рамках предложенного алгоритма можно получить более точную модель, с большей степенью нелинейности относительно исходных молекулярных параметров, а именно:
PC = 61.3-6.38x9+0.11(x1)2x5x9-0.02x9 (x1)2(x8)2
(δср = 1.42%, s = 0.634, R = 0.9515).
4. Все модели, отобранные как наилучшие, содержат 3 структурных параметра (если их рассматривать как линейные) и обладают очень высоким коэффициентом корреляции. Опираясь на классификацию моделей по коэффициенту корреляции, приведенную в [5], их можно охарактеризовать, по крайней мере, как «очень хорошие».
Частоты появления в корреляциях различных инвариантов
Весьма интересным представляется вопрос о том, какие из рассмотренных, формально определенных инвариантов наиболее часто встречаются в построенных корреляциях и с чем может быть связана их «популярность». Для ответа на этот вопрос были найдены суммарные частоты появления всех 9 рассмотренных инвариантов во всех 8 корреляциях (линейных и нелинейных, полученных отдельно для матриц М1-М4) для каждого свойства (табл. 2). Частота встречаемости инварианта в отдельной корреляции определялась как число его появлений в соответствующей формуле, с учетом степени этого инварианта. Например, для приведенной выше корреляции для РС частоты появления x1, x5, x8, x9 равны 4, 1, 2, 3 соответственно.
Таблица 2
Суммарные частоты появления параметров х1-х9 во всех 8 корреляциях
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
|
|
bp |
1 |
4 |
4 |
1 |
5 |
7 |
1 |
0 |
6 |
|
MV |
4 |
4 |
5 |
0 |
4 |
5 |
0 |
0 |
9 |
|
MR |
3 |
4 |
2 |
2 |
2 |
5 |
0 |
0 |
12 |
|
HV |
4 |
3 |
1 |
2 |
5 |
6 |
1 |
1 |
8 |
|
TC |
5 |
3 |
3 |
2 |
3 |
6 |
0 |
2 |
7 |
|
PC |
7 |
4 |
0 |
1 |
1 |
2 |
6 |
0 |
8 |
|
ST |
2 |
2 |
1 |
3 |
3 |
10 |
5 |
2 |
6 |
|
Σ |
26 |
24 |
16 |
11 |
23 |
41 |
13 |
5 |
56 |
Оказалось, что наиболее «популярные» 3 инварианта – это x9, х6, х1: x9 = n; x6 = ∑1 / λi, λi >0; x1 = max λi. Эти факты можно объяснить, например, следующим образом.
Параметр x9 = n может служить количественной характеристикой размера молекулы, а размер молекулы существенно влияет на ее свойства (например, чем больше размер молекул, тем больше энергии необходимо затратить, чтобы начался процесс кипения или испарения соответствующего вещества).
Параметр x1 может служить мерой ветвления молекулярного графа-дерева (в случае матрицы смежности), так как при фиксированном n он принимает свои экстремальные значения на наиболее и наименее разветвленных графах (с интуитивной точки зрения) – графе-звезде и графе-цепи. Чем больше «ветвистость» МГ, тем сильнее молекулы «цепляются» друг за друга своими ветвями, тем больше энергия взаимодействия молекул и тем выше, например, температура кипения.
Нами установлено, что параметр 1/x6 (для матрицы смежности) совместно с инвариантом Р3, равным числу цепочек длины 3 в МГ, хорошо коррелирует с плотностью ρ соответствующих веществ (коэффициент корреляции R = 0,965). Итак, x6 связан определенным образом с плотностью веществ, а она, в свою очередь, существенно влияет на многие другие свойства алканов. Например, для ρ можно получить довольно точную двухпараметрическую корреляцию с Р3 и bp или с Р3 и HV (R = 0,97); при добавлении в уравнение третьего параметра n коэффициент корреляции увеличивается: R = 0,99.
Нелинейные корреляции на основе спектров всех четырех матриц
Кроме того, для всех рассматриваемых свойств были построены нелинейные модели, для построения которых использовались параметры х1-х8 не для какой-либо одной матрицы, как выше, а для всех четырех, а также х9 (т.е. всего 33 исходных параметра). Назовем такие модели обобщенными.
Цель построения обобщенных моделей – выяснить: 1) можно ли таким образом улучшить результаты, полученные ранее для отдельных матриц; 2) будут ли использоваться в них все рассмотренные матрицы или только наилучшая, выявленная ранее.
Для вышеуказанных обобщенных моделей была проведена проверка их адекватности при помощи так называемой процедуры скользящего контроля (cross validation). Суть этой процедуры заключается в следующем: из исходной выборки, состоящей из N структур, удаляют одну структуру, затем строят новую модель на оставшихся структурах, далее при помощи этой модели рассчитывают величину свойства для удаленной структуры; эти действия выполняют для всех N структур, а затем строят корреляцию между экспериментальными и рассчитанными значениями изучаемого свойства. По статистическим характеристикам этой корреляции (например, по коэффициенту корреляции и среднеквадратичному отклонению) делают вывод о качестве тестируемой модели.
В таблице 3 представлены результаты построения и тестирования нелинейных обобщенных моделей для всех семи физико-химических свойств. В ней указаны параметры, вошедшие в корреляцию, а также соответствующие матрицы, по которым они вычислялись; кроме того, приведены значения некоторых статистических характеристик полученных моделей: δср – средняя относительная ошибка (в %), s – среднеквадратичное отклонение, R – коэффициент корреляции. При этом параметр R указан с четырьмя знаками после запятой, как и в таблице 1, для того чтобы можно было сравнивать модели из таблиц 1 и 3 по этому параметру.
Таблица 3
Результаты построения и тестирования нелинейных обобщенных моделей
|
Инварианты МГ, вошедшие в корреляцию |
δср (%) |
s |
R |
δср,cv (%) |
scv |
Rcv |
|
|
bp |
x5(М1)x3(М1), (x6(М2))2, x5(М4)x6(М2) |
2.18 |
2.65 |
0.9928 |
2.60 |
2.99 |
0.990 |
|
MV |
х1(М4)x4(M1), х4(М4)x8(М2), x3(М3)x6(М3) |
0.40 |
0.79 |
0.9979 |
0.73 |
1.39 |
0.994 |
|
MR |
x9, x2(М4)x4(М3), х5(M1)x6(М2) |
0.10 |
0.05 |
0.9999 |
0.10 |
0.04 |
0.999 |
|
HV |
x5(M1)x5(М4), x8(М2)x4(М2), x8(M1) x8(М4) |
0.83 |
0.40 |
0.9948 |
1.37 |
0.61 |
0.989 |
|
TC |
x5(M1)x1(M1), x6(M1)x7 (М3), x8(М4)x7(М3) |
1.14 |
4.14 |
0.9876 |
1.47 |
4.86 |
0.981 |
|
PC |
x5(M1)x6(М2),x8(М4)x74(М3), x6(М2)x6(M1) |
1.03 |
0.41 |
0.9802 |
1.64 |
0.69 |
0.931 |
|
ST |
x5(M1)x7(M1), x2(М4)x4(М3), x6(M1)х1(М3) |
1.21 |
0.33 |
0.9785 |
1.65 |
0.44 |
0.956 |
Кроме того, в таблице 3 приведены аналогичные результаты для процедуры скользящего контроля, выполненной для полученных моделей: δср,cv – средняя относительная ошибка (в %), scv – среднеквадратичное отклонение, Rcv – коэффициент корреляции.
Сравнивая модели в таблицах 1 и 3 по величине коэффициента корреляции R, можно сделать вывод, что для каждого физико-химического свойства полученная обобщенная модель является более точной, чем наилучшая из предыдущих восьми, построенных для каждой из матриц М1-М4 отдельно. Результаты скользящего контроля свидетельствуют о хорошей стабильности полученных моделей.
Кроме того, установлено, что для четырех свойств (bp, HV, TC, ST) в корреляциях используются 3 матрицы, а для трех (MV, MR, PC) – все 4 матрицы (из четырех). Таким образом, практически все рассмотренные матрицы оказались полезными при моделировании связи «структура – свойство». Заметим, что при этом параметр x9 = n вошел в корреляцию только для свойства MR.
Выводы
1. В работе предложен новый подход к моделированию связи между физико-химическими свойствами алканов и их структурными характеристиками. Одна из особенностей разработанной методики – это использование в качестве молекулярных параметров только инвариантов спектрального типа соответствующих МГ. Вторая особенность – применение гибкой итерационной процедуры построения аппроксимирующей функции в моделях связи «структура – свойство», которая является многочленом специального вида от исходных молекулярных параметров.
2. Показано, что для ряда физико-химических свойств алканов разработанный подход позволяет строить достаточно точные модели связи «структура – свойство». При сравнении результатов, получаемых для разных четырех видов матриц МГ, установлено, что наилучший результат дает матрица смежности МГ. Использование для построения корреляций одновременно всех инвариантов всех рассмотренных четырех матриц позволяет улучшить результаты, получаемые для каждой матрицы отдельно. При этом полезными оказываются все матрицы.
3. При проведении статистического анализа частоты встречаемости различных молекулярных параметров в построенных корреляциях (по отдельным матрицам) выявлены 3 наиболее «популярных» параметра и предложено качественное объяснение этим фактам.
4. Предлагаемый подход к построению корреляций «структура – свойство» допускает обобщение путем расширения перечня используемых спектральных инвариантов или/и рассмотрения дополнительно каких-либо других матриц МГ, что может способствовать увеличению его эффективности. Получаемые корреляции могут быть также улучшены за счет увеличения степени их нелинейности. Отметим также, что разработанная методика моделирования связи «структура – свойство» может быть применена к органическим соединениям любого класса и любым свойствам, измеряемым количественно.



