Единая система современного образования предполагает применение на всех ее уровнях для всех групп учащихся наиболее эффективных методологий обучения. В настоящее время одним из таких подходов является моделирование образовательных траекторий с помощью методов математического моделирования. Они позволяют наиболее гибко адаптировать учебный процесс под каждого обучаемого при такой наиболее распространенной форме классно-урочной системы школьного образования, как групповая работа [1, 2]. Методология моделирования образовательных траекторий оптимальными способами открывает широкие возможности дифференциации процесса обучения с учетом личностных запросов школьника [3, 4]. Данный подход оказывается перспективным и в работе с одаренными детьми при их подготовке к олимпиадному программированию.
Олимпиадное программирование является одной из ветвей дидактической линии обучения алгоритмизации и программирования в школьном курсе информатики. Оно составляет предмет углубленного обучения школьников. При этом, как правило, обучение в данном направлении ведется с наиболее одаренными детьми в области математики и информатики. Так, в школе «Ступени к Олимпу», образовательная деятельность в которой осуществляется по всем школьным дисциплинам, основу группы школьников, обучаемых олимпиадному программированию, образуют участники профильных олимпиад по информатике и учащиеся, прошедшие профотбор в школе дистанционного обучения одаренных детей при Смоленском областном институте развития образования (СОИРО). При этом специфика образовательного процесса такова, что в этой школе при обучении олимпиадному программированию нет возрастного деления на группы. Учащиеся занимаются подготовкой в данной предметной области совместно. В связи с этим возникает естественный вопрос об организации учебного процесса оптимальным образом.
Цель исследования – описание и анализ применения методов математического моделирования при формировании индивидуальных траекторий обучения олимпиадному программированию.
Научная новизна состоит в применении методологий математического моделирования, а именно методов функционального анализа, как средства построения оптимальных образовательных траекторий при обучении школьников олимпиадному программированию.
Материалы и методы исследования
Олимпиадное программирование выступает особым направлением в общей системе обучения информатике в школе. Оно предполагает, с одной стороны, владение собственно методами программирования, которые позволяют в выбранной инструментальной системе реализовать алгоритм решения задачи. С другой стороны, знание только основ алгоритмизации и синтаксиса среды программирования, как правило, не обеспечивает решение поставленной проблемы надлежащим образом с учетом особенностей всех входящих данных, что отражается в наборах для тестирования программы [5]. Иными словами, школьнику необходима такая подготовка, которая в том числе состоит в объяснении математических способов решения и иллюстрации их записи в изучаемой им системе программирования. В то же время в обучении олимпиадному программированию достаточно часто наблюдаются две ситуации. В первой из них школьник владеет синтаксисом записи структур и алгоритмов в инструментальной среде разработки программ, но не может математически полно и грамотно решить задачу. Во второй он может выработать ход решения задачи, но не может подобрать инструменты для реализации. Первая ситуация в большей степени свойственна учащимся средней школы, а вторая – старшей школы. В отдельных, но не исключительных случаях наоборот. Ввиду совместной подготовки при решении олимпиадных задач уже данные факторы обуславливают с необходимостью поиск оптимального выбора образовательных траекторий, как для общих групп обучения, так и для совершенствования индивидуального мастерства школьников в программировании. Именно поэтому методы математического моделирования выступают средством обеспечения и претворения в жизнь данных идей в повседневной практике.
Еще одним фактором, обуславливающим использование методов математического моделирования в процессе обучения олимпиадному программированию, является его периодичность. Во многом приобретение профессиональных навыков носит самостоятельный характер, который обеспечивается еженедельной подготовкой, тренировками в олимпиадных раундах на различных онлайн-платформах и участием в отраслевых олимпиадах школьников. Так в школе «Ступени к Олимпу» обучение ведется сессиями, во время которых обучаемым школьникам рассказывается теоретический материал о подходах решения разных классов задач и демонстрируется их программная реализация. В межсессионный период учащиеся самостоятельно оттачивают приобретенные навыки программирования математических алгоритмов на разнообразных задачах практики в индивидуальном темпе. В связи с этим обойтись в рамках организованного таким образом образовательного процесса без применения средств математического моделирования траекторий обучения невозможно. Отказ от их использования приводит не только к снижению результатов освоения дидактической линии олимпиадного программирования, но и снижению интереса к такой деятельности, а следовательно, к оттоку обучаемых из групп школьников, прошедших профессиональный отбор.
В качестве средств математического моделирования образовательных траекторий можно использовать разные подходы. Так, научная школа под руководством С.П. Грушевского предлагает внедрять интерактивные модели планирования образовательного процесса и применять фасетные технологии в процессе формирования профессиональных компетенций учителей информатики [6, 7]. В работах Д.А. Бояринова предлагается использовать семантические сети и фреймовые структуры для формализации учебного материала, а также инварианты теории графов для формирования набора индивидуальных заданий в системе адаптивного непрерывного образования [8, 9]. В педагогических исследованиях О.М. Киселевой описывается модель и методология группового обучения на основе подбора оптимальных математических моделей изучения предметного материала. Она успешно переносит методы математического моделирования на формат дистанционного обучения, который в условиях современной системы образования незаменим как инструмент организации самостоятельной работы [10, 11].
В данном исследовании инструментами математического моделирования служат:
1. Представление предметной области изучаемого материала в виде семантической сети [12]. Это обусловлено двумя факторами. Во-первых, совокупность логических закономерностей и причинно-следственных связей между элементами знаний, как правило, не является линейно-иерархической структурой. Во-вторых, при формировании групповых и индивидуальных траекторий обучения как средство оптимального моделирования используется модифицированная семантическая сеть с измененным набором элементов знаний и их взаимосвязями. Такой формат позволяет добавлять или удалять структурные элементы семантической сети, гибко адаптируя ее под текущие характеристики изучения предметного материала.
2. Выявление латентных характеристик системы изучаемого материала, которые определяют знания школьников на текущем этапе обучения, с помощью математического аппарата соответствия Галуа [13]. Во-первых, данный выбор основан на том, что ключевую роль в преодолении барьеров при изучении дисциплинарных знаний играют внутренние факторы индивидуального освоения учебных предметных модулей. Во-вторых, выявление общих закономерностей в характере и темпе изучения учебного материала с использованием методологии соответствия Галуа обеспечивает моделирование подвижных мини-групп обучаемых олимпиадному программированию школьников.
3. Формирование индивидуальных и групповых наборов изучения компонентов учебного материала с использованием аппарата математических критериев импликативных матриц [14]. Во-первых, система критериев моделирования по заданным параметрам одновременно служит инструментом адаптивного учета личностных запросов учащихся и средством реализации образовательного процесса в зоне ближайшего развития обучаемых. Во-вторых, импликативный выбор позволяет прогнозировать и определять степень достижимости результатов обучения на заданном временном интервале с фиксированными вероятностными показателями освоения предметных модулей учебной дисциплины.
Итак, обучение школьников олимпиадному программированию с использованием методов математического моделирования проводилось в соответствии со следующей парадигмой. Для каждой сессии интенсивных недельных занятий был подобран исходный теоретический и практический материал, который составлял основу изучаемого модуля. Так, например, на сессии входных лекций и практических работ по олимпиадному программированию изучались такие базовые вопросы, как основные типы данных, файловый ввод-вывод данных, линейные программы, формирование массивов, организация и использование циклов. После чего рассматривались задачи, требующие знаний по динамическому программированию, процедурам и функциям и рекурсивным подпрограммам при соответствующем изложении теоретического материала алгоритмических подходов. На второй сессии школьникам объясняли материал по обработке фиксированной последовательности чисел, обработке числовых последовательностей, расчету площади под кривой, обработке цифр в строке на необходимом наборе задач, иллюстрирующих методы их программной реализации. Третья сессия состояла в изучении вопросов множественного типа данных, основных методов сортировки, методов быстрой сортировки, а также разборе решения ключевых задач на клеточной карте и задач на шахматной доске. Четвертая сессия включала решение задач в прямоугольной системе координат, задач на кодирование данных в системах счисления, задач на перебор множеств и задач на графах с необходимыми теоретическими пояснениями. Данная сессия была итоговой. После нее проводилась итоговая олимпиада школьников по программированию проекта «Ступени к Олимпу».
Всем школьникам в рамках обучения на каждой сессии предлагался базовый учебный материал. После его изучения вне зависимости от возраста учащихся проводилось диагностическое тестирование, которое было направлено на формирование групп дальнейшего обучения в сессионный период и генерирование индивидуальных траекторий в межсессионное время. В силу разных базовых математических знаний такой подход был единственно оптимальным при организации обучения. Также отметим и такую особенность, как владение школьниками навыками программирования в различных инструментальных средах. Базовыми являлись языки программирования PascalABC.NET, Python и C++, а также в отдельных случаях C# и Java. При этом акцент в объяснении делался на содержательном изложении материала. Синтаксис используемой в реализации алгоритма системы программирования изучался уже в рамках подвижных групп обучения и индивидуально. Данные особенности обусловили как необходимое условие использование такого подхода в обучении олимпиадному программированию, как математическое моделирование образовательных траекторий. При этом одинаковый возраст и выбор системы программирования при решении задач также являлись одними из критериев формирования мини-групп обучения. В то же время ключевыми факторами служили исходный уровень способностей, текущий уровень учебных достижений и латентные параметры освоения учебного материала, выявленные с помощью применения соответствия Галуа при диагностических тестированиях и выполнении заданий практики.
В межсессионное время каждый школьник, как правило, самостоятельно тренировался в решении практических задач и совершенствовал навыки в олимпиадном программировании. Консультирование проводилось с периодом в две недели и состояло в оценке текущего уровня учебных достижений обучаемых для коррекции траекторий обучения, причем как индивидуальных, так и групповых. Обучаемые олимпиадному программированию школьники ввиду индивидуального графика могли изучать предметный материал в собственном темпе с учетом иной своей занятости в ежедневном образовательном процессе средней школы. Именно такой подход позволял не только не снижать интерес к данной области знаний, но и систематически подкреплять его и выводить уровень владения навыками олимпиадного программирования на новый профессиональный уровень.
Результаты исследования и их обсуждение
Педагогический эксперимент по внедрению методологий математического моделирования в обучение олимпиадному программированию осуществляется ежегодно на протяжении последних пяти лет в школе «Ступени к Олимпу». Обучение проводится на базе Смоленского государственного университета совместно со Смоленским областным институтом развития образования. Информационная поддержка и профотбор школьников для обучения на основе подготовленных материалов осуществляется дистанционно на базе информационно-методического портала СОИРО. Олимпиадному программированию в школе «Ступени к Олимпу» обучается ежегодно от 15 до 20 школьников Смоленской области. Экспериментальная работа проводится с использованием автоматизированной интеллектуальной системы «Advanced Tester». В данной системе на основе введенных данных об элементах обучения автоматически генерируется семантическая сеть предметного материала, проводятся диагностические и итоговые тестирования уровня учебных достижений, формируются оптимальные образовательные траектории с помощью математического аппарата соответствия Галуа и импликативных матриц. В данном программном комплексе оценка уровня индивидуальных учебных достижений школьника и групповых результатов обучения предполагает использование средств диагностики современной теории тестовых измерений. Анализ полученных экспериментальных данных осуществляется автоматически в непрерывном режиме, что обеспечивает функционал интеллектуальной программной среды «Advanced Tester» [15]. Обоснование необходимости использования функциональных методов математического моделирования как инструмента построения оптимальных образовательных траекторий при обучении школьников олимпиадному программированию отражено в обобщенных результатах педагогического эксперимента за пять лет, в ходе которого в нем приняли участие 88 школьников.
Количественный анализ экспериментальных данных проводился по формуле
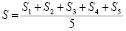 ,
,
где S1 – теоретические вопросы, а S2, S3, S4, S5 – задания практики олимпиадного программирования. Оценивание проводилось по шкале в 100 баллов. Обобщенные результаты итоговых ежегодных диагностических работ школьников по знанию теоретических подходов к решению олимпиадных задач и владению навыками их программной реализации в инструментальной среде представлены в таблице.
Результаты педагогического эксперимента по обучению школьников олимпиадному программированию также отражены на рисунке.
Результаты обучения школьников олимпиадному программированию
|
Группа |
Число школьников, достигших уровня усвоения знаний |
Всего |
||
|
Высокий |
Повышенный |
Базовый |
||
|
Экспериментальная группа 1 |
6 |
8 |
1 |
15 |
|
Экспериментальная группа 2 |
7 |
9 |
1 |
17 |
|
Экспериментальная группа 3 |
8 |
9 |
2 |
19 |
|
Экспериментальная группа 4 |
8 |
9 |
2 |
19 |
|
Экспериментальная группа 5 |
7 |
10 |
1 |
18 |
|
Всего |
36 |
45 |
7 |
88 |
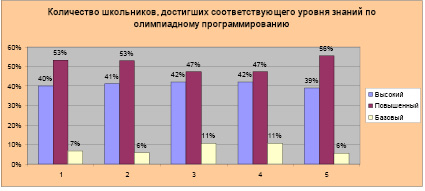
Результаты обучения школьников олимпиадному программированию
Качественный анализ условий и результатов эксперимента
Количественные данные учебных достижений школьников по обучению олимпиадному программированию с применением методов математического моделирования демонстрируют смещение кривой нормального распределения в область высоких результатов. Учащиеся, освоившие программу учебной дисциплины на базовом уровне, составляют единицы от всех обучаемых олимпиадному программированию. Этот факт можно объяснить тем, что область решения олимпиадных заданий требует индивидуального подхода при обучении школьников. Организация работы в подвижных мини-группах с учетом индивидуальных особенностей является оптимальным решением при изучении олимпиадного программирования. Восприятие школьниками специальных приемов решения задач, мышление на уровне абстрактных структур данных определяют дифференциацию учебного процесса таким образом, что индивидуальный темп освоения учебного материала становится нормой обучения. Таким образом, упор на самостоятельный характер учебной деятельности с контактным обучением в мини-группах является ответом на образовательный запрос подготовки школьников в области решения олимпиадных задач по программированию. При этом без использования методологий математического моделирования решить эффективным способом данную проблему в реалиях временных ограничений практически невозможно. Ввиду вышесказанного гипотеза, выдвинутая в проводимом исследовании, находит свое подтверждение в экспериментальной деятельности авторов.
Заключение
Данные о непрерывном педагогическом эксперименте, проводимом последние пять лет, наглядно демонстрируют эффективность организации обучения олимпиадному программированию выбранным способом. Использование автоматизированного программного комплекса «Advanced Tester» для моделирования образовательных траекторий показывает востребованность таких интеллектуальных инструментов математического моделирования. Формализация компонентов учебного материала открывает возможности дифференцированного варьирования взаимосвязями между ними. Исследование межэлементных связей в свою очередь позволяет оперировать упорядоченными наборами данных, оказывающими существенное влияние на различные характеристики процесса обучения. Это открывает перспективы формирования образовательных траекторий в соответствии с поставленными задачами обучения с необходимым учетом индивидуальных запросов в области профессионального программирования. Таким образом, обучение олимпиадному программированию с использованием математического моделирования путей обучения в единой образовательной карте школьника приобретает оптимальный характер, который определяет положительный ответ на вопрос подготовки специалистов в IT-индустрии на высоком профессиональном уровне.



