Использование современных цифровых технологий (СЦТ) находит свое применение во всех сферах образования. Одной из них является строительная отрасль, где при изучении дисциплин естественнонаучного цикла применение СЦТ наиболее актуально. В том числе при решении различных математических задач в подготовке будущих строителей [1–3]. Направлений использования СЦТ можно отметить несколько:
− поддержка графики;
− поддержка сметных работ;
− поддержка информационного моделирования;
− поддержка математического моделирования.
Для поддержки графики цифровые технологии стали использоваться достаточно давно. Еще в 1960-х гг. разрабатываются первые графические устройства (например, SketchPad), создаются первые электронные чертежные машины. А в конце 1970-х гг. была представлена первая система описания здания (Building Description System). В настоящее же время представлено множество программных продуктов, которые позволяют создавать строительные инженерные чертежи, документацию, реализовывать трехмерную графику и т.д.
Программы, поддерживающие работу со сметами, выполняют автоматизированную сметную оценку проектам, расчет в потребностях в ресурсах и т.д. Примерами таких программ могут выступать Дизайн Интерьера, ГРАНД-Смета, АванСмета, Смета+, WinСмета и т.д.
Следующее направление – информационное моделирование – представлено технологией Building Information Modeling (BIM), которая стала внедряться в США с 2003 г. С помощью BIM технологий могут быть получены виртуальная модель здания, индивидуальные параметры объекта; качественная проектная документация и т.д.
Последнее направление, связанное с решением математических задач в строительной сфере с помощью СЦТ, более подробно освещено в нашем исследовании.
Таким образом, цель исследования – рассмотреть возможности использования СЦТ при решении математических задач для студентов строительных специальностей.
Материалы и методы исследования
В качестве цифрового инструментария в исследовании предлагается использовать программный пакет R-Studio.
R – статистическая система анализа, созданная Россом Ихакой и Робертом Гентлеманом (1996, J. Comput. Граф. Stat., 5: 299–314). R является и языком, и программным обеспечением [4, 5].
Система статистического анализа и визуализации данных R состоит из следующих основных частей:
− языка программирования высокого уровня R, позволяющего одной строкой реализовать различные операции с объектами, векторами, матрицами, списками и т.д.;
− большого набора функций обработки данных, собранных в отдельные так называемые «пакеты»;
− развитой системы поддержки, включающей обновление компонентов среды, интерактивную помощь и различные образовательные ресурсы, предназначенные как для начального изучения R, так и для последующих консультаций по возникающим затруднениям.
Язык R может быть установлен на различных операционных системах, включая Windows, Unix, Linux и Mac OS. Удобным средством вычислений в R является RStudio. RStudio представляет собой бесплатную интегрированную среду разработки (IDE) для R. Благодаря ряду своих особенностей, этот активно развивающийся программный продукт делает работу с R очень удобной. В сложившейся ситуации использование свободного программного обеспечения особенно актуально и в перспективе использование RStudio может стать альтернативой другим математическим пакетам, в том числе и MS Excel.
С точки зрения решаемых в исследовании задач важной возможностью системы организации расчета основных параметров описательной статистики, а также расчет всех трех коэффициентов корреляции, критерия Стьюдента и т.д.
Математическая обработка данных является главной задачей любого вида деятельности. Она лежит в основе любой технической задачи. Современные цифровые технологии помогают получить быстрый результат любых длительных математических расчетов, получить необходимую точность вычисления [6]. В качестве примера мы взяли одну из математических задач строительной отрасли и применили к ней данную методику использования программного пакета R-Studio.
Пример 1. Определить прямую регрессию, определяющую зависимость коэффициента теплопроводности λ, Вт / (м2 ⋅ °С) жаростойкого бетона с заполнителем из магнезита от средней температуры нагрева t °С по данным эксперимента, приводимым в табл. 1.
Таблица 1
Данные для выполнения задания
|
t oC |
100 |
300 |
600 |
700 |
900 |
110 |
|
λ |
5,90 |
5,35 |
4,78 |
4,20 |
3,60 |
3,00 |
|
m |
2 |
3 |
3 |
4 |
4 |
2 |
Рассмотрим решение примера в программе RStudio.
Данную таблицу представим в виде csv-файла в ЭТ Excel (рис. 1).
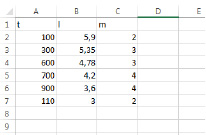
Рис. 1. Вид файла в ЭТ Excel
Затем считаем в программу
T<-read.csv2(“11.csv”, header=TRUE, sep=”;” , dec = “,”);
Вид таблицы представлен на рис. 2.
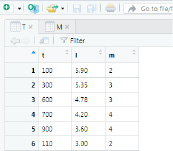
Рис. 2. Вид данных в R Studio
Вычислим коэффициент корреляции для переменных t и l.
Для вычисления корреляции в RStudio используется команда cor. В нашем случае имеем
cor(T$t, T$l)
Рассчитанное значение представлено на рис. 3.

Рис. 3. Результаты вычислений в R Studio
Значение коэффициента корреляции -0.9930041 указывает на сильную связь между переменными.
Далее перейдем к вычислению парной линейной регрессии, для вычисления которой используется функция lm.
regF2F1<-lm(formula=T$l ~T$t)
Выведем информацию о регрессии (рис. 4).
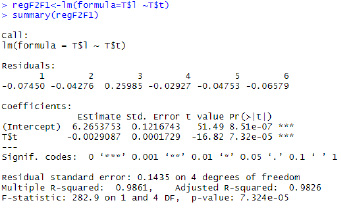
Рис. 4. Результаты вычислений в R Studio
Multiple R-squared: 0,9861, то есть коэффициент детерминации равен 0,97 – близок к 1. Проверим значимость регрессии p-value = 7.324e-05 < 0,1, следовательно, регрессия значима.
Далее перейдем к описанию полученных коэффициентов регрессии.
p-value для свободного члена (Intercept) = 8,51e-07 < 0,1, следовательно, свободный член значим. p-value для коэффициента при переменной (T$t) = 7,32e-05< 0,1, следовательно, коэффициент при переменной значим. Таким образом, делаем вывод о значимости обоих коэффициентов регрессии.
Уравнение примет вид
l = 6.2653753-0.0029087t.
Для построения графика регрессии воспользуемся командой abline.
abline(regF2F1, col=»red»)
Вид графика представлен на рис. 5.
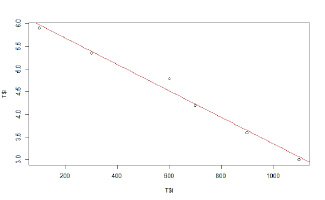
Рис. 5. Вид графика
Также можно найти относительную ошибку аппроксимации MAPE (рис. 6).

Рис. 6. Вид вычислений
Относительная ошибка аппроксимации равна 1,951416 %. Следовательно, полученную регрессию можно использовать для прогнозирования.
Рассмотрим следующий пример.
Пример 2. Проанализируем среднюю стоимость квадратного метра жилья в России за 2017, 2018, 2019 гг.
Вид данных представлен на рис. 7.
Определить вид нелинейной регрессии.
Построим несколько нелинейных регрессий для переменных.
Для начала построим график линейной регрессии, аналогично примеру 1.
Вид полученного графика представлен на рис. 8.
Уравнение примет вид
y = 52740,80 + 201,07x.
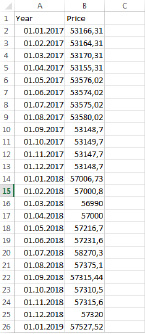
Рис. 7. Вид данных в ЭТ Excel
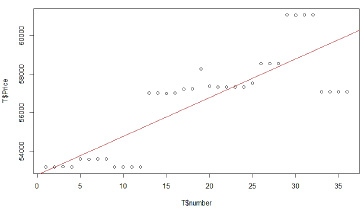
Рис. 8. Вид графика
Вычисления в RStudio выглядят следующим образом (рис. 9).
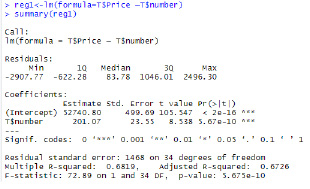
Рис. 9. Вид вычислений
Найдем относительную ошибку аппроксимации MAPE (рис.10).
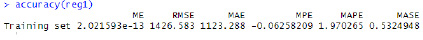
Рис. 10. Вид вычислений
Вычислим нелинейные регрессии (рис. 11, 12).
y = p1 + p2ln(x) + ε.
reg2<-lm(formula=T$Price ~log(T$number))
Рис. 11. Вид вычислений
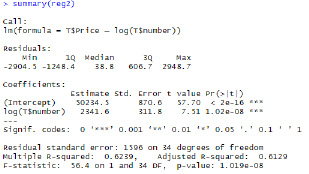
curve(coef(reg2)[1] + coef(reg2)[2]*log(x), add=TRUE, col=”green
«)
Рис. 12. Вид вычислений
Он примет вид, представленный на рис. 13.
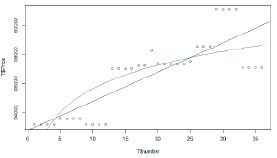
Рис. 13. Вид графика
Найдем относительную ошибку аппроксимации MAPE (рис. 14).
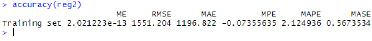
Рис. 14. Вид вычислений
Исследуем регрессию вида y = p1 + p2x + p3x2 + p43 (рис. 15).
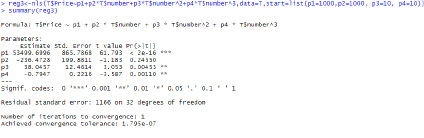
Рис. 15. Вид вычислений
Построим график (рис. 16).
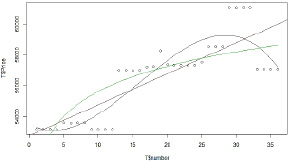
Рис. 16. Вид графика
Таблица 2
Результаты опроса
|
Варианты |
1 курс |
2 курс |
||
|
Кол-во |
% |
Кол-во |
% |
|
|
Использование стандартного математического аппарата |
10 |
50,0 % |
5 |
17,9 % |
|
Использование стандартного математического аппарата с организацией вычисления с использованием СЦТ |
4 |
20,0 % |
8 |
28,6 % |
|
Решение полностью с использованием СЦТ |
6 |
30,0 % |
15 |
53,6 % |
Нами был разработан элективный курс «Использование современных цифровых технологий в решении математических задач» для специальностей 07.03.01 Архитектура, 07.03.04 Градостроительство, 08.03.01 Строительство, который в данный момент разрабатывается в Пензенском государственном университете архитектуры и строительства. Дальнейшие исследования связаны с апробацией данного элективного курса.
Результаты исследования и их обсуждение
В течение 2020–2022 учебного года данная методика была апробирована на занятиях по высшей математике на специальностях 07.03.01 Архитектура, 07.03.04 Градостроительство, 08.03.01 Строительство. Студентам предлагались различные математические задачи строительного профиля. Были предложены следующие варианты решения:
− использование стандартного математического аппарата;
− использование стандартного математического аппарата с организацией вычислением с использованием СЦТ;
− решение полностью с использованием СЦТ.
В результате в конце курса был проведен опрос среди 58 студентов 1 и 2 курса обучения. Результаты опроса представлены ниже (табл. 2).
Как видно из табл. 2, отмечается увеличение процента студентов с 30,0 % до 53,6 %, которые предпочитают решение задач полностью с использованием СЦТ. В то же время отметим резкое уменьшение процента студентов до 17,9 %, которые предпочитают решение задач с использованием стандартного математического аппарата. Таким образом, можно сделать вывод, что использование СЦТ при решении математических задач обретает популярность, что объясняется теми преимуществами, которые они обеспечивают. Так же очевидно, что дальнейшее использование СЦТ будет более широким. Поэтому требуется методическая работа по разработке адекватного задачного материала.
Заключение
В результате проведённого исследования были отмечены несколько направлений использования СЦТ при решении математических задач при подготовке будущих строителей. Большее внимание в результате было уделено направлению, связанному с решением математических задач в строительной сфере с помощью СЦТ. В качестве информационного инструментария была выбрана программная среда R-Studio.



