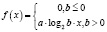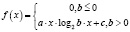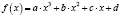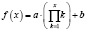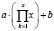К настоящему времени разработано множество электронных ресурсов [1], предназначенных для автоматизации проверки решений задач по программированию. В большинстве случаев они ориентированы на спортивное программирование, но также находят применение при обучении программированию в школах, колледжах и высших учебных заведениях. Зачастую такие ресурсы ограничиваются проверкой корректности решения и его способности выдать результат за заранее определённое время. Этого более чем достаточно для соревновательного программирования, но для облегчения работы преподавателя в ходе проведения практикумов по программированию для школьников и студентов мог бы оказаться полезным более подробный отчёт. Помимо других пунктов, характеризующих решение, такой отчёт должен включать информацию об эффективности алгоритма, предложенного обучающимся.
Чтобы судить об эффективности алгоритма, необходимо оценить его временную и пространственную сложность. Временная сложность определяется количеством элементарных операций, совершаемых алгоритмом для решения поставленной задачи. Пространственная сложность характеризуется объемом затраченной памяти. Для оценки обеих характеристик применятся нотация «О» большое [2, с. 12], ставшая популярной после того, как в 1976 году Дональд Кнут предложил её использование для анализа алгоритмов.
Таблица 1
Наиболее распространённые категории сложности алгоритмов по времени
|
№ |
Название |
Оценка |
Пример |
|
1 |
Константное время |
О(1) |
Умножение числа на два |
|
2 |
Линейное время |
О(n) |
Нахождение суммы элементов массива |
|
3 |
Логарифмическое время |
О(log2n) |
Бинарный поиск |
|
4 |
Линейно-логарифмическое время |
О(n∙log2n) |
Сортировка слиянием |
|
5 |
Квадратичное время |
О(n2) |
Сортировка пузырьком |
|
6 |
Кубическое время |
О(n3) |
Подбор корней уравнения с четырьмя неизвестными |
|
7 |
Экспоненциальное время |
О(2n) |
Нахождения множества всех подмножеств |
|
8 |
Факториальное время |
О(n!) |
Решение задачи коммивояжёра полным перебором |
Нотация «О» большое описывает сложность алгоритма в виде функции от объёма входных данных. Поскольку эта функция должна давать примерную оценку наихудшего возможного времени выполнения алгоритма, для неё берут только самый высокий порядок переменной и не берут константные коэффициенты. Например, если требуется выполнить поиск элемента в отсортированном массиве, то наихудшее время выполнения алгоритма бинарного поиска будет оцениваться как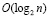 
, где n – количество элементов в массиве.
Существует несколько наиболее распространённых категорий сложности алгоритмов по времени, каждая из которых характеризуется собственной О-нотацией. В учебных задачах чаще всего встречаются категории, приведённые в таблице 1.
В данном исследовании предпринимается попытка предложить способ автоматического определения категории сложности алгоритма, применённого студентом для решения задачи по программированию на языке Python. С этой целью рассматривается механизм трассировки, как источник данных для дальнейшего анализа методом приближения с помощью кривых.
Материалы и методы исследования
Программный код решений задач зачастую содержит блоки, ответственные за чтение входных данных и вывод результатов, что может исказить результаты анализа решения. Так, если от студента требуется реализовать алгоритм бинарного поиска, сложность которого определяется логарифмической функцией, то основные временные затраты придутся на чтение входных данных – процесс, описываемый линейной функцией. Чтобы корректно оценить решение задачи как имеющее временную сложность О(log2n), необходимо оценивать только фрагмент кода, осуществляющего основную обработку данных.
Поиск основного алгоритма в программном коде решения задачи может представлять собой проблему, которая серьёзно упростится, если сформулировать задание особым образом. Например, студенту можно предложить закончить частично написанную программу, в которой уже реализованы загрузка входных данных и вывод результатов.
Одним из возможных способов определения категории сложности алгоритма является его трассировка, в ходе которой в реальном времени собирается статистика о выполняемых им действиях. В отличие от других методов, таких как статический анализ программного кода, трассировка легко осуществима, особенно в интерпретируемых языках. Например, язык программирования Python предоставляет функцию sys.settrace, позволяющую задать обработчик, который будет вызываться при переходе к каждой следующей строке программы. Анализ этих вызовов позволяет оценить количество выполненных в программе итераций циклов, а следовательно, и собрать статистику о временной сложности выполняющегося алгоритма.
Результаты исследования и их обсуждение
График на рисунке 1 показывает пример расчёта сложности сортировки массива методом «пузырька» и статистику, полученную путём подсчёта количества итераций во время трассировки. Как видно из графика, прогнозируемая и полученная кривые имеют схожую форму, отличие объясняется тем, что сортировка выполнялась на массиве, заполненном случайными данными, в то время как оценочная формула О(n2) даёт прогноз по наихудшему случаю. Для метода «пузырька» наихудшим случаем является массив, отсортированный в порядке, обратном требуемому. При тестировании на таком массиве различие между кривыми было бы менее заметным. Однако, для цели оценки, полученного результата достаточно, поскольку требуется определить категорию алгоритма, а не получить точную кривую.
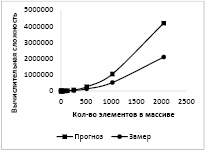
Рис. 1. Прогноз и результаты замера вычислительной сложности алгоритма сортировки массива методом «пузырька»
Аналогично рассмотренному алгоритму были выполнены замеры для примеров алгоритмов №№ 3-8 из таблицы 1. Полученные результаты вместе с использованными исходными кодами разработанного программного обеспечения доступны в виде дополнительных материалов на GitHub (https://github.com/irinaby/bigO).
Следующим этапом после тестирования алгоритмов и сбора статистики о количестве итераций является выбор наиболее подходящей категории для каждого из них. Поскольку категории задаются функциями от количества обрабатываемых элементов, задачу подбора категории можно решить, выбрав кривую, наиболее точно аппроксимирующую полученные результаты измерений. Для этого была выбрана функция scipy.optimize.curve_fit из пакета SciPy [3], использующая алгоритм TRF (Trust Region Reflective) [4]. Такой подход даёт оптимальные результаты аппроксимации при малом количестве выполненных измерений, что позволит минимизировать необходимое количество циклов тестирования решения и повысить производительность тестирующей системы образовательного ресурса. Функции, для которых осуществлялся подбор коэффициентов, приведены в таблице 2. После подстановки коэффициентов в функции было выполнено вычисление выдаваемого ими прогноза для каждого из тестов. Данные, полученные для всех рассмотренных алгоритмов, доступны в дополнительных материалах к данной статье.
Таблица 2
Функции, применённые для аппроксимации результатов подсчёта количества итераций
|
Категория |
Использованная функция |
Реализация на Python |
|
Константное время |
f(x) = a |
def constFn(x, a): return [a] * len(x) |
|
Линейное время |
f(x) = k ∙ x + b |
def linearFn(x, a, b): return a * x + b |
|
Логарифмическое время |
|
def logarithmicFn(x, a, b, c): if (b <= 0): return [0] * len(x) return a * log2(b * x) + c |
|
Линейно-логарифмическое время |
|
def linearithmicFn(x, a, b, c): if (b <= 0): return [0] * len(x) return a * x * log2(b * x) + c |
|
Квадратичное время |
f(x) = a ∙ x2 + b ∙ x + c |
def quadraticFn(x, a, b, c): return a * x**2 + b * x + c |
|
Кубическое время |
|
def cubicFn(x, a, b, c, d): return a * x**3 + b * x ** 2 + c * x + d |
|
Экспоненциальное время |
f(x) = a ∙ 2b ∙ x + c |
def exponentialFn(x, a, b, c): return a * power(2, b * x) + c |
|
Факториальное время |
|
def factorialFn(x, a, b): return list(a * prod(range(1, int(k)+1)) + b for k in x) |
Таблица 3
Результаты трассировки решения задачи коммивояжёра и прогноз функций, дающих наиболее точную аппроксимацию
|
n – кол-во городов |
Кол-во итераций |
||
|
трассировка |
a = 1,000001517 b = 3,887447327 |
a ∙ 2b ∙ x + c a = 0,00036394 b = 3,3214786 c = 657,832586 |
|
|
1 |
1 |
4,88 |
657,83 |
|
2 |
3 |
5,88 |
657,86 |
|
3 |
8 |
9,88 |
658,19 |
|
4 |
27 |
27,88 |
661,46 |
|
5 |
124 |
123,88 |
694,17 |
|
6 |
725 |
723,88 |
1021,09 |
|
7 |
5046 |
5043,89 |
4289,34 |
|
8 |
40327 |
40323,94 |
36961,60 |
|
9 |
362888 |
362884,43 |
363582,48 |
|
10 |
3628809 |
3628809,39 |
3628773,92 |
Для примера рассмотрим решение задачи коммивояжёра [5, с. 176] методом полного перебора. Имеются результаты десяти тестов, начиная с одного города и далее до десяти, с шагом один. Количество итераций, определённое при трассировке, а также прогнозы двух функций, давших наилучшую аппроксимацию, приведены в таблице 3.
На рисунке 2 приведена визуализация данных из таблицы 3.
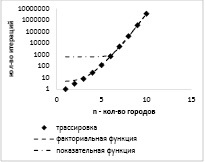
Рис. 2. Визуализация результатов трассировки решения задачи коммивояжёра и прогнозы функций, дающих наиболее точное приближение
Ромбами обозначены результаты замера количества выполненных итераций. Штрихами и штрих-пунктиром показаны графики двух функций, давших наилучшие результаты приближения. Заметно, что кривая, полученная для функции факториала (штрихи), дала наилучший результат, в то время как показательная функция (штрих-пунктир) заметно отклоняется при малых значениях n.
Для определения наиболее подходящих функций был применён метод RMSE (1), в силу квадратичной природы которого даже небольшие ошибки в предсказаниях аппроксимирующих функций оказывают существенное влияние на получаемые оценки. Это особенно важно при работе с такими функциями, как показательная или факториал, поскольку они дают значительный прирост значения при небольшом увеличении аргумента.
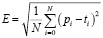, (1)
где Е – среднеквадратичная ошибка, N – количество проведённых тестов, pi – предсказанные значения, ti – результаты трассировки.
После выполнения серии тестов для алгоритмов №№ 3-8 из таблицы 1 была предпринята попытка подбора коэффициентов для каждой из функций в таблице 3. Результаты вычисления оценки RMSE для всех пар алгоритм-функция приведены в таблице 4. Ячейки пар, давших наилучшие совпадения, выделены тёмным фоном. Выполнить подбор коэффициентов для показательной функции удалось только для алгоритмов, работающих с относительно небольшим количеством входных данных (n <= 32).
Таблица 4
Оценка методом RMSE прогнозов аппроксимирующих функций
|
Алгоритм O(n) |
Бинарный поиск |
Сортировка слиянием |
Сортировка пузырьком |
Подбор корней уравнения с четырьмя неизвестными |
Нахождение множества всех подмножеств |
Решение задачи коммивояжёра полным перебором |
|
Константное время |
146.90 |
205697358.8 |
1.19⋅1012 |
6.15⋅1011 |
2.78⋅1011 |
3.69⋅1012 |
|
Линейное время |
92.16 |
469462.27 |
91524960974 |
84025107392 |
1.71⋅1011 |
2.48⋅1012 |
|
Логарифмическое время |
6.58 |
90342184.8 |
7.32⋅1011 |
2.352⋅1011 |
2.25⋅1011 |
3.04⋅1012 |
|
Линейно-логарифмическое время |
470.02 |
57.20 |
6499875441 |
8518378383 |
1.03⋅1011 |
1.59⋅1012 |
|
Квадратичное время |
289.90 |
35251.08 |
1.30⋅10-21 |
1736469909 |
77628512124 |
1.28⋅1012 |
|
Кубическое время |
3592.00 |
14156682.39 |
1.74⋅10-20 |
2.16⋅10-21 |
26071065573 |
4.99⋅1011 |
|
Экспоненциальное время |
переполн. |
переполн. |
переполн. |
переполн. |
5.46⋅10-21 |
4579076.11 |
|
Факториальное время |
146.20 |
205693163.9 |
1.19⋅1012 |
5.56⋅1011 |
1.90⋅1011 |
17.59 |
При больших значениях n вычисление показательной функции приводит к ошибке переполнения. Это не является проблемой, поскольку сам факт возникновения переполнения говорит о неприменимости функции к алгоритму.
Заключение
По результатам проделанной работы видно, что трассировка алгоритмов помогает получить необходимые данные для подбора коэффициентов аппроксимирующих функций методом приближения с помощью кривых. Также удалось показать, что применение метода RMSE для сравнения выдаваемых функциями оценок с результатами трассировки позволяет с высокой точностью определить категорию сложности алгоритма. Однако следует помнить, что многие языки программирования содержат функции, предназначенные для обработки большого количества данных за одну операцию. Оценить категорию сложности решений, использующих такие функции, одним лишь предложенным методом невозможно. Одним из путей преодоления этого препятствия является применение статического анализа кода, что может стать темой дальнейших исследований в данном направлении.
Преимуществами предложенного метода определения категории сложности являются простота его реализации и независимость от производительности системы, на которой выполняется тестирование, поскольку подсчитывается количество итераций циклов, а не время выполнения программного кода, получаемые результаты оказываются значительно более точными. Также следует отметить, что рассмотренные в работе алгоритмы и категории сложности являются наиболее часто встречающимися в учебных материалах по программированию. Вместе с тем существуют и другие, которые также имеет смысл рассмотреть на применимость предлагаемого метода оценки, особенно случаи, когда решение задачи требует последовательно применить несколько различных алгоритмов.