Моделирование является основным инструментом для анализа и повышения эффективности в организации функционирования транспортных потоков. Вопросы оптимального управления логистическими системами регионов являются весьма актуальными в настоящее время, что связано с возрастающими объемами транспортных корреспонденций. Поэтому для управления транспортными потоками необходимо использовать современные методы построения и обновления матриц, которые будут учитывать особенности исследуемого региона, а также вероятностные характеристики системы.
Для построения матрицы корреспонденций исследуемый регион разбивают на N районов и находят корреспонденции между i-м и j-м районами, где i, j=1,…,N.
Библиографический поиск показал, что интерес к данной проблеме достаточно велик у коллективов отечественных и зарубежных авторов. Так, например, в работе [1] обсуждаются вопросы моделирования логистических процессов в Арктической зоне Российской Федерации, а также производится анализ существующих моделей, где выявляется, что Арктический регион имеет существенные особенности для применения данных моделей; в [2] описаны основные методы и модели построения матриц транспортных корреспонденций; в статье [3] выявлены критерии устойчивости и надежности транспортных систем; в статье [4] раскрыта возможность построения матрицы транспортных корреспонденций с помощью больших данных, получаемых посредством мобильного телефона; вопросы, связанные с применением беспроводных сенсорных систем для управления городским транспортом, описаны в работе [5].
Обычно при формировании матриц, корреспонденции представляют в виде действительных чисел, что не позволяет учитывать неоднородность и нечеткость входной информации. Анализ позволил выявить, что современные методы моделирования сталкиваются с проблемой получения корреспонденций, так как их необходимо определять опосредованно. В явном виде они не являются наблюдаемыми. При получении корреспонденций приходится работать с большим количеством неоднородных данных, которые необходимо затем привести к единому формату для построения моделей транспортных систем. При этом необходимо учитывать достаточное количество факторов, которые влияют на значения корреспонденций. К таким факторам относятся результаты анкетирования населения об их передвижении, информация о социально-экономической ситуации в исследуемом регионе, данные о билетах для оплаты проезда и так далее. Возникает задача извлечения знаний из полученных данных. С извлечением знаний чаще всего работают эксперты, которые вносят своё субъективное решение в полученную информацию. Представить полученные знания в виде некоторой случайной величины также не всегда представляется возможным, так как для эмпирических данных сложно подобрать известную функцию распределения. Именно поэтому методологию нечетких отношений удобно использовать для получения матрицы корреспонденции.
Целью данного исследования является модификация моделей построения матриц корреспонденций экстраполяционными методами за счет применения к ним нечетких характеристик, которые позволят учесть неоднородность и нечеткость данных, входящих в модель транспортной системы.
Материалы и методы исследования
Среди методов построения матриц корреспонденций выделяют экстраполяционные, вероятностные и реляционные методы. К наиболее простым для реализации методам относятся экстраполяционные методы или, как их ещё называют, методы коэффициентов роста.
В качестве исходной информации обычно используют фактические величины корреспонденций между транспортными узлами региона и прогноз их роста [2]. При этом прогноз определяется экспертами, поэтому все данные удобнее представить в виде нечетких чисел.
В рамках теории нечетких множеств под нечетким числом понимается некоторое расширение классического множества на множество действительных чисел. В классическом множестве принадлежность элемента к множеству имеет точное значение: 0 или 1, то есть можно с достоверной вероятностью сказать, принадлежит ли элемент множеству. В нечетком множестве значение функции принадлежности может принимать значения от 0 до 1. При этом если значение меньше 0,5, то элемент скорее не принадлежит множеству, если больше, чем 0,5, то элемент скорее принадлежит множеству. Если значение функции принадлежности равно 0,5, то эксперт, определяющий принадлежность элемента к нечеткому множеству, находится в затруднении и эта точка является точкой перехода.
Пусть U – универсальное множество, μА(и) – функция, определенная на множестве U и принимающая значения на отрезке [0,1]. Тогда пара (U, μА(и)) называется нечетким множеством A, а функция μА(и) является функцией принадлежности нечеткого множества A [6].
Общая форма записи нечеткого подмножества для случаев, когда U конечно или счетно, имеет вид
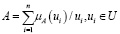
Оперируя нечеткими числами, необходимо определить функцию принадлежности. Эти функции подразделяются на два больших класса: непрерывные и дискретные. При работе с эмпирическими данными удобнее использовать дискретные функции принадлежности, так как это упрощает расчеты и сокращает вычислительные ресурсы. Среди дискретных функций принадлежности самой часто используемой в практике за счет своей простоты является треугольная функция. Поэтому при составлении матриц корреспонденций будем использовать класс так называемых треугольных нечетких чисел.
Треугольное нечеткое число W представляет собой тройку чисел (cl, a, cr), где а – центр, cl – это величина нечеткости слева, cr – это величина нечеткости справа. Число а – мода или четкое значение нечеткого треугольного числа, а cl и cr определяют степень размытости четкого числа.
Треугольному нечеткому числу W соответствует нечеткое множество A, функция принадлежности которого определена на множестве R+ и имеет вид
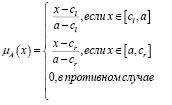
Если W1 и W2 – два треугольных нечетких числа, заданных тройками чисел (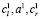
) и (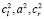
) соответственно. Тогда операции между этими числами будут производиться в соответствии со следующими правилами:
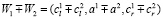
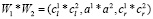
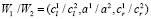
При этом результат выполнения операций (сложения, вычитания, умножения и деления) над треугольными числами будет являться треугольным числом, то есть всегда будет выполняться условие замкнутости [7].
Результаты исследования и их обсуждение
Одним из наиболее простых экстраполяционных методов является метод с единственным коэффициентом роста. Данный коэффициент определяется как отношение общих прогнозируемых корреспонденций к общим фактическим корреспонденциям [2]. Таким образом, коэффициент роста К также будет нечетким треугольным числом, зависящим от таких показателей, как уровень дохода населения, количество населения в регионе, уровень автомобилизации и других [2].
Рассмотрим построение матрицы корреспонденций методом единственного коэффициента роста с использованием нечетких треугольных чисел между N транспортными узлами. Каждый элемент матрицы является нечетким треугольным числом
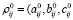), i = 1,…,N, j = 1,…,N
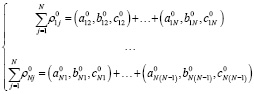
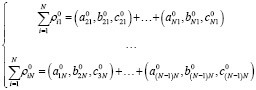
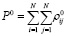
Общий объем прогнозных значений также будет выражаться нечетким треугольным числом.
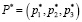
Коэффициент роста K = (k1,k2,k3) – нечеткое треугольное число вычисляется в виде отношения
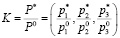
Затем строим матрицу прогнозных корреспонденций, где
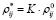, i = 1,…,N, j = 1,…,N
Все элементы полученной матрицы также будут представлять собой нечеткие треугольные числа.
Метод единственного коэффициента не позволяет учитывать динамику системы, обладает низкой достоверностью и используется только для проектирования отдельных регионов на ближайшую перспективу.
Использование нечетких чисел при расчете транспортных корреспонденций позволит учесть неопределенность и получить более реалистичную оценку значений матрицы.
Если величины корреспонденций будут определяться экспертами и представляться в виде треугольных нечетких чисел, то соответственно величины прогнозируемых корреспонденций также будут представлять собой треугольные числа, и определяться как произведение количества фактических корреспонденций, относящихся к определенному участку транспортной сети, на коэффициент роста [2].
Более точные прогнозные матрицы корреспонденций позволяет получить метод, основанный на методе средних коэффициентов роста. Данный метод также опирается на информацию, полученную при анализе фактических корреспонденций. Однако здесь вычисляется не общий коэффициент, а среднее арифметическое между коэффициентами i-го и j-го транспортных районов, то есть
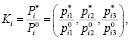
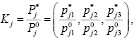i,j = 1,…,N
где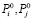 
– объемы общих фактических корреспонденций;
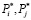– объемы общих прогнозируемых корреспонденций.
Для нахождения прогнозных корреспонденций на первом шаге будем использовать формулу:
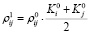, i = 1,…,N, j = 1,…,N,
,
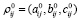В данном случае при нахождении прогнозных корреспонденций необходимо будет использовать свойства суммы и умножения нечетких треугольных чисел, а также деления нечеткого числа на четкое. В результате объемы корреспонденций на первом шаге также получаются треугольными числами. При нахождении прогнозных корреспонденций на некотором шаге k необходимо будет воспользоваться итерационной формулой.
Данный метод связан с большими расчетами по сравнению с методом единственного коэффициента роста, однако он позволяет учесть неравномерность в темпах роста различных районов в исследуемом регионе. Следует отметить, что при достаточно большом росте подвижности населения вышеописанный метод даст слишком большую погрешность.
Объединение вышеописанных методов получило название детройтский метод. В данном методе учитываются не только коэффициенты роста каждого района, но и коэффициент роста, общий для всего исследуемого региона. В этом случае величина прогнозных коэффициентов на каждом шаге будет определяться как произведение корреспонденций на предыдущем шаге на отношение произведения коэффициентов роста для i-го и j-го региона на предыдущем шаге на общий коэффициент роста.
Недостаток данного метода заключается в том, что в случае большой разницы между отдельно взятым районом и регионом в целом, прогнозные значения матрицы корреспонденции будут иметь слишком большое отклонение от реальности.
Наибольшее распространение из всех экстраполяционных методов получил метод Фратара. В данном методе, помимо коэффициентов роста для i-го и j-го районов, в расчете прогнозных корреспонденций участвуют коэффициенты роста корреспонденций в зоне m, обусловленного развитием зон i и j. При этом процесс также является итерационным. Корреспонденции от каждого последующего шага зависят от предыдущей итерации.
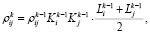
где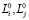 
– коэффициенты роста корреспонденций в зоне m, m = 1,…,N. Данные коэффициенты также будут представляться тройками чисел.
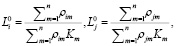
где Km – коэффициент развития для зоны m.
Для окончания процесса моделирования рассчитывается величина, равная заранее заданному значению транспортного оборота. При этом на каждой итерации производится сравнение полученной суммы прогнозных корреспонденций региона с данным значением. Итерационный процесс заканчивается в случае, когда достигается равенство указанных величин.
При использовании нечетких чисел, в расчетах коэффициентов роста и развития регионов, корреспонденции также будут являться нечеткими числами с треугольной функцией распределения. Данный метод является самым трудоемким среди остальных экстраполяционных методов, однако именно он дает наиболее точные результаты. Учитывая, что наложение нечетких отношений на входные данные ещё более усложнит расчеты, для моделирования матриц корреспонденций заданным методом необходимо использование программного обеспечения.
Заключение
Среди известных методов построения матриц корреспонденций экстраполяционные методы являются наиболее простыми для расчетов, однако обладают недостатками, связанными с получением моделей, не учитывающих нечеткость и неоднородность входных данных. Они не позволяют строить модели на долгосрочную перспективу.
Использование нечетких чисел при расчете транспортных корреспонденций, безусловно, усложняет расчеты, появляется необходимость применения свойств нечетких чисел, а также необходимость работы с матрицами, где элементы матриц также будут нечеткими. Учитывая данный факт, необходимо проводить дополнительные исследования, связанные с проверкой устойчивости матриц к воздействиям.
Однако применение методологии нечетких отношений позволит учесть неопределенность и субъективизм экспертов в оценке корреспонденций и даст более гибкую оценку значениям корреспонденций.
Работа выполнена в рамках темы ФНИР «Трансформация социокультурного пространства регионов Арктической зоны Российской Федерации в современных условиях» № государственной регистрации 122012100405-4.