Постановка вопроса. В существующих арифметико-логических устройствах используются операции с плавающей точкой, а при сложении мантисс применяются схемы вычисления переноса. То и другое ограничивает длину разрядной сетки. Это отрицательно влияет на точность вычислений и кроме того ограничивает быстродействие вычислительной системы вследствие последовательного тактирования выполнения переноса. В работе ставится вопрос о возможности выполнения арифметических операций без вычисления переноса, что позволило бы их выполнять параллельно по всем разрядам операндов с удлиненной разрядной сеткой. Излагаемый подход опирается на методы [1–3], которые существенно корректируются, в частности, для адаптации к произвольной длине разрядной сетки.
Цель работы – показать возможность эквивалентного обычной арифметике выполнения арифметических операций без вычисления переноса и оценить потенциал роста производительности и снижения погрешности вычислительной обработки на этой основе.
Исходные соотношения. Групповая обработка потока слагаемых. Вначале излагается подход к обработке слагаемых, его особенности используются в дальнейшем как основа метода в целом. Пусть требуется определить значение произвольно взятой частичной суммы Sp ряда 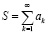 (неограниченного потока) из (n+1)-разрядных целочисленных двоичных слагаемых
(неограниченного потока) из (n+1)-разрядных целочисленных двоичных слагаемых
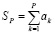 , (1)
, (1)
где
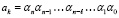 (2)
(2)
и
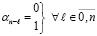 . (3)
. (3)
Слагаемые (1) разбиваются на группы с произвольно фиксированным количеством N слагаемых в группе. Пусть, например, в (1)–(3) P = 16, n+1 = 4, и
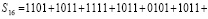
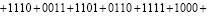
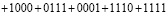 . (4)
. (4)
Слагаемые (4) слева направо разбиваются на группы по N = 4 в порядке расположения. Первая группа
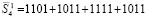
обрабатывается следующим образом:
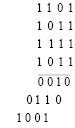 (5)
(5)
В (5) слагаемые группы 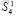 располагаются друг под другом, в каждом столбце по вертикали находятся коэффициенты разрядов одинакового веса. В каждом столбце коэффициенты суммируются независимо от всех других столбцов (суммирование выполняется параллельно и синхронно по всем столбцам):
располагаются друг под другом, в каждом столбце по вертикали находятся коэффициенты разрядов одинакового веса. В каждом столбце коэффициенты суммируются независимо от всех других столбцов (суммирование выполняется параллельно и синхронно по всем столбцам):
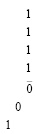
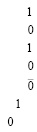
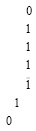
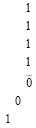 (6)
(6)
Сумма элементов каждого столбца (6) записывается (под чертой) в позиционном двоичном коде по возрастанию веса справа налево, со смещением по диагонали сверху вниз. Так, сумма элементов четвертого столбца, состоящего из четырех единиц (веса младшего разряда 20), имеет запись 4 = 1 × 22 + 0 × 21 + 0 × 20 = 100, которая смещена по диагонали справа налево, сверху вниз. Аналогично, сумма элементов третьего столбца, состоящего из нуля и трех единиц (веса 21), имеет двоичную запись 3 = 0 × 22 + 1 × 21 + 1 × 20 = 011, которая с сохранением веса каждого разряда аналогично смещена от столбца по диагонали. Сумма элементов второго столбца 010 смещена аналогично предыдущим. Сумма элементов первого столбца 100 смещена аналогично. Смещение каждой позиционной записи суммы элементов столбца выполняется так, что коэффициенты взаимно однозначно располагаются по весу вертикального столбца своего и последующих разрядов. Все смещения геометрически параллельны, и двоичные коды сумм столбцов не налагаются друг на друга. Математически эти коды в совокупности образуют три промежуточных слагаемых в горизонтальной позиционной записи, сумма которых остается невычисленной. Предполагается, что каждый бит промежуточных слагаемых сохраняет одна ячейка памяти (триггер). Образуется три горизонтальных линейки триггеров, соответственных горизонтальным записям трех промежуточных слагаемых ниже черты в (5). Количество 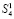 горизонтальных линеек (ниже промежуточных рядов, синоним – промежуточных слагаемых) равно максимальному числу разрядов двоичной суммы вертикального столбца. В данном случае
горизонтальных линеек (ниже промежуточных рядов, синоним – промежуточных слагаемых) равно максимальному числу разрядов двоичной суммы вертикального столбца. В данном случае 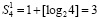 , где [α] – целая часть α. Если бы разбиение в (1)–(4) было выполнено по произвольному количеству N слагаемых, то число промежуточных рядов составило бы
, где [α] – целая часть α. Если бы разбиение в (1)–(4) было выполнено по произвольному количеству N слагаемых, то число промежуточных рядов составило бы 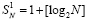 . В излагаемом варианте метода
. В излагаемом варианте метода 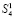 промежуточных слагаемых отдельно не суммируются. Они подсоединяются к следующей группе слагаемых входного потока (4). Именно, вторая группа
промежуточных слагаемых отдельно не суммируются. Они подсоединяются к следующей группе слагаемых входного потока (4). Именно, вторая группа 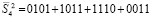 с подсоединением
с подсоединением 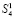 промежуточных слагаемых обрабатывается следующим образом:
промежуточных слагаемых обрабатывается следующим образом:
 (7)
(7)
Слагаемые промежуточных рядов под чертой в (7) формируются совершенно аналогично тому, как описано выше для (5), с той единственной разницей, что выше черты расположено не 4 слагаемых, а 7 – за счет подсоединения к входной группе дополнительных 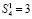 промежуточных слагаемых из (5). И снова количество
промежуточных слагаемых из (5). И снова количество 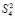 промежуточных рядов на выходе под чертой оказалось равным 3. Очевидно, это потому, что на входе в (7) было
промежуточных рядов на выходе под чертой оказалось равным 3. Очевидно, это потому, что на входе в (7) было 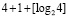 слагаемых, на выходе обработки под чертой появилось
слагаемых, на выходе обработки под чертой появилось 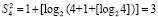 слагаемых (по максимальному числу разрядов двоичной суммы элементов столбца). Если бы разбиение в (1)–(4) было выполнено по произвольно фиксированному количеству N слагаемых, то число промежуточных рядов составило бы
слагаемых (по максимальному числу разрядов двоичной суммы элементов столбца). Если бы разбиение в (1)–(4) было выполнено по произвольно фиксированному количеству N слагаемых, то число промежуточных рядов составило бы 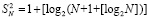 . Как и на предыдущем этапе
. Как и на предыдущем этапе 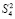 промежуточных ряда отдельно не суммируются, они подсоединяются к следующей группе
промежуточных ряда отдельно не суммируются, они подсоединяются к следующей группе 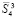 слагаемых входного потока (4). Именно, третья группа
слагаемых входного потока (4). Именно, третья группа 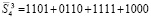 с подсоединением
с подсоединением 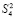 промежуточных слагаемых из (7) обрабатывается следующим образом:
промежуточных слагаемых из (7) обрабатывается следующим образом:
 (8)
(8)
Замечание 1. В дальнейшем нулевые старшие разряды промежуточных слагаемых не записываются, поскольку не влияют на сумму. Технически исключить их запись можно на основе оценки роста числа разрядов промежуточных слагаемых. Такая оценка дана в [1], уточнена в [4] и будет представлена ниже.
Промежуточные ряды под чертой в (8) формируются в полной аналогии тому, как описано для (7). Их количество снова равно 3: в (8) над чертой было 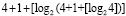 слагаемых, под чертой оказалось
слагаемых, под чертой оказалось 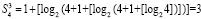 . В случае разбиения по N, число промежуточных рядов составило бы
. В случае разбиения по N, число промежуточных рядов составило бы 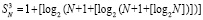 .
.
Как и прежде 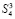 промежуточных ряда отдельно не суммируются, а подсоединяются к следующей группе
промежуточных ряда отдельно не суммируются, а подсоединяются к следующей группе 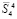 слагаемых входного потока (4). Заключительная четвертая группа
слагаемых входного потока (4). Заключительная четвертая группа 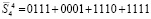 с подсоединением
с подсоединением 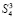 промежуточных рядов из (8) обрабатывается следующим образом:
промежуточных рядов из (8) обрабатывается следующим образом:
 (9)
(9)
Слагаемые промежуточных рядов под чертой в (9) сформированы аналогично тому, как описано для (8). Их количество снова равно 3:
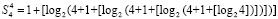 .
.
При разбиении по N получилось бы
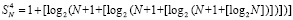 .
.
Повторяя процесс применительно к промежуточным рядам, их можно сжать в два промежуточных ряда, затем окончательно просуммировать.
Рассмотренный процесс сложения можно продолжать неограниченно. Если сколь угодно увеличить число слагаемых в (4), то число промежуточных рядов всегда будет равно трем. В общем случае суммы (1) с произвольным значением P описанному алгоритму соответствует рекуррентная формула количества промежуточных рядов:
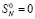 ,
,  ,
,
(10)
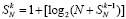 ,
, 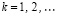
В (10) предполагается разбиение (1) на группы по N, k – номер шага алгоритма.
Содержание каждого шага необходимо пояснить. Именно, операции суммирования во всех столбцах выполняются параллельно и синхронно на соответственных процессорных элементах. Это разрядные процессорные элементы, взаимно независимые по всем разрядам данных, с постоянными линиями связи для каждого столбца, поэтому не требующие обмена. Запись результатов сложения коэффициентов в столбце выполняется параллельно и синхронно по всем столбцам, не требует вычисления переноса. Обработка каждого столбца состоит в сложении двоичных коэффициентов веса одного фиксированного разряда (сложение бит разрядного среза, суммирование по вертикали). Выполнять такое суммирование можно либо на процессорных элементах, коммутируемых по схеме сдваивания, либо на сопоставленной столбцу логической схеме, либо на параллельном сдвигателе с шифратором [2]. Одна из схем приводится в дальнейшем. Во всех таких схемах длительность tc сложения элементов столбца измеряется логарифмическим числом переключений логических элементов, tc = O(log2N) [2], что определяет время выполнения шага алгоритма соответственного (10). Все преобразования слагаемых (1) эквивалентны обычной арифметике, поэтому использование алгоритма в архитектуре вычислительной системы не влечет отказ от последовательного программирования.
Соотношения (10) по номерам шагов разворачиваются в виде
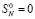 ,
, 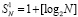 ,
, 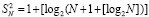 ,
,
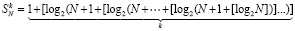 , k = 1, 2, … (11)
, k = 1, 2, … (11)
Пусть z = N + 1. Тогда из (11)
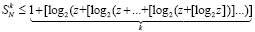 .
.
Поскольку 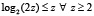 , то
, то 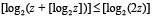 , и
, и
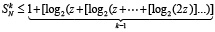 . (12)
. (12)
Если правую часть (12) обозначить 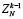 , то с учетом
, то с учетом 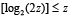 получится
получится
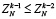 ,
, 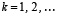 (13)
(13)
Последовательная подстановка в (12) неравенств (13) по индукции влечет 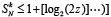 , или,
, или,
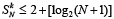 ,
, 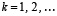 (14)
(14)
С учетом (11), (14) имеет место
Теорема 1. Пусть Sp (1) вычисляется посредством рассматриваемого алгоритма, соответственного (10). Тогда, каковы бы ни были P ≥ 2 и N ≥ 2 в разбиении набора слагаемых (1) на группы по N, точное число 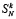 промежуточных рядов на шаге k ≥ 1 определяется из (11). Значение
промежуточных рядов на шаге k ≥ 1 определяется из (11). Значение 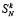 ограничено из (14) константой, которая зависит только от N, в частности, не зависит от номера шага k и от числа разрядов слагаемых n+1.
ограничено из (14) константой, которая зависит только от N, в частности, не зависит от номера шага k и от числа разрядов слагаемых n+1.
Теорема уточняет аналогичное утверждение из [1] и означает, что число шагов алгоритма формально может быть неограниченным.
Следствие 1. В условиях теоремы 1 количество 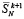 входных слагаемых на шаге равно
входных слагаемых на шаге равно
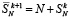
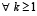 , (15)
, (15)
где 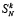 определяется из (11) и ограничено согласно (14).
определяется из (11) и ограничено согласно (14).
О границах роста старших разрядов промежуточных слагаемых. На первом шаге рассматриваемого алгоритма вычисления (1) прирост 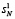 ненулевых старших разрядов промежуточных рядов по отношению к числу разрядов (2) не превышает числа промежуточных рядов, точнее, ограничен из неравенства
ненулевых старших разрядов промежуточных рядов по отношению к числу разрядов (2) не превышает числа промежуточных рядов, точнее, ограничен из неравенства 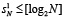 . Речь идет именно о приросте числа старших разрядов. На нем не сказывается наличие «нулевого» разряда вертикального среза, поэтому, в отличие от (11), добавлять единицу в правую часть последней оценки не нужно. На втором шаге прирост будет определяться вертикальным суммированием именно уже приросших разрядов промежуточных рядов, что оценивается как
. Речь идет именно о приросте числа старших разрядов. На нем не сказывается наличие «нулевого» разряда вертикального среза, поэтому, в отличие от (11), добавлять единицу в правую часть последней оценки не нужно. На втором шаге прирост будет определяться вертикальным суммированием именно уже приросших разрядов промежуточных рядов, что оценивается как 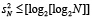 и т.д. На некотором шаге останется не больше двух ненулевых старших разрядов, подлежащих вертикальному суммированию, и после очередного шага суммирования прирост составит не более чем один разряд. На последующих шагах единичный прирост не увеличится, причем будет происходить не на каждом шаге. Этой оценкой можно было бы ограничиться, однако она представляет собой формальное препятствие для роста длины разрядной сетки. Трудность можно обойти с учетом особенностей вертикального суммирования потока слагаемых. Пусть, для удобства изложения,
и т.д. На некотором шаге останется не больше двух ненулевых старших разрядов, подлежащих вертикальному суммированию, и после очередного шага суммирования прирост составит не более чем один разряд. На последующих шагах единичный прирост не увеличится, причем будет происходить не на каждом шаге. Этой оценкой можно было бы ограничиться, однако она представляет собой формальное препятствие для роста длины разрядной сетки. Трудность можно обойти с учетом особенностей вертикального суммирования потока слагаемых. Пусть, для удобства изложения, 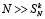 . На первом шаге алгоритма обработки потока все старшие разряды промежуточных рядов из числа
. На первом шаге алгоритма обработки потока все старшие разряды промежуточных рядов из числа 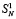 , имеющие вес больше чем 2n, предлагается отсоединить в отдельный набор слагаемых, и на втором шаге они не обрабатываются. На втором шаге все старшие разряды промежуточных рядов из числа
, имеющие вес больше чем 2n, предлагается отсоединить в отдельный набор слагаемых, и на втором шаге они не обрабатываются. На втором шаге все старшие разряды промежуточных рядов из числа 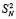 , имеющие вес больше, чем 2n, также отсоединяются в отдельный набор, который располагается над аналогичным набором предыдущего шага. При этом по вертикали располагаются коэффициенты равного между собой веса отсоединенных слагаемых текущего и предыдущего наборов. Такое накопление отсоединенных слагаемых выполняется на каждом шаге k ≥ 1, пока их количество не приблизится (не превышая) к правой части оценки (15). По окончании накопления весь набор отсоединенных слагаемых поразрядно-параллельно обрабатывается за один шаг точно так, как описано выше для набора из
, имеющие вес больше, чем 2n, также отсоединяются в отдельный набор, который располагается над аналогичным набором предыдущего шага. При этом по вертикали располагаются коэффициенты равного между собой веса отсоединенных слагаемых текущего и предыдущего наборов. Такое накопление отсоединенных слагаемых выполняется на каждом шаге k ≥ 1, пока их количество не приблизится (не превышая) к правой части оценки (15). По окончании накопления весь набор отсоединенных слагаемых поразрядно-параллельно обрабатывается за один шаг точно так, как описано выше для набора из 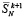 входных слагаемых. Для определенности считается, что такой шаг выполнен на параллельно работающих разрядных процессорных элементах без прерывания основной обработки потока слагаемых (возможен вариант с прерыванием основной обработки). В результате образуются промежуточные ряды с весом разрядов, превосходящим 2n, количество таких рядов не больше
входных слагаемых. Для определенности считается, что такой шаг выполнен на параллельно работающих разрядных процессорных элементах без прерывания основной обработки потока слагаемых (возможен вариант с прерыванием основной обработки). В результате образуются промежуточные ряды с весом разрядов, превосходящим 2n, количество таких рядов не больше 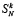 из (14). К таким промежуточным рядам снова добавляются отсоединенные слагаемые от каждого шага обработки основного набора. Процесс продолжается до образования нового входного набора, количество слагаемых которого приблизится (не превышая) к правой части оценки (15). Затем снова выполняется шаг сжатия полученного набора до промежуточных рядов и т.д. В продолжение шагов обработки веса разрядов просуммированных отсоединенных слагаемых будут возрастать, и старший разряд достигнет веса 2(n+1)+n = 22n+1 В случае превышения этого веса разряды всех промежуточных рядов, образованных отсоединенными слагаемыми, снова отсоединяются, теперь уже в новый отдельный набор. В новом наборе они накапливаются и обрабатываются, как в предыдущем наборе отсоединенных промежуточных рядов. При этом обработка предыдущего отсоединенного набора и основного набора продолжается без изменения и без прерывания. По достижении в новом наборе веса разрядов 22n+1+n = 23n+1 разряды большего веса снова, аналогично предыдущему, отсоединяются в отдельный набор, который обрабатывается в полной аналогии предыдущему. Рассматриваемый процесс иллюстрирует диаграмма (рис. 1).
из (14). К таким промежуточным рядам снова добавляются отсоединенные слагаемые от каждого шага обработки основного набора. Процесс продолжается до образования нового входного набора, количество слагаемых которого приблизится (не превышая) к правой части оценки (15). Затем снова выполняется шаг сжатия полученного набора до промежуточных рядов и т.д. В продолжение шагов обработки веса разрядов просуммированных отсоединенных слагаемых будут возрастать, и старший разряд достигнет веса 2(n+1)+n = 22n+1 В случае превышения этого веса разряды всех промежуточных рядов, образованных отсоединенными слагаемыми, снова отсоединяются, теперь уже в новый отдельный набор. В новом наборе они накапливаются и обрабатываются, как в предыдущем наборе отсоединенных промежуточных рядов. При этом обработка предыдущего отсоединенного набора и основного набора продолжается без изменения и без прерывания. По достижении в новом наборе веса разрядов 22n+1+n = 23n+1 разряды большего веса снова, аналогично предыдущему, отсоединяются в отдельный набор, который обрабатывается в полной аналогии предыдущему. Рассматриваемый процесс иллюстрирует диаграмма (рис. 1).

Рис. 1. Схема раздельного запоминания и вертикальной обработки старших разрядов промежуточных слагаемых
На рис. 1 каждый этап группового поразрядно-параллельного сложения соответствует шагу алгоритма вертикальной обработки набора слагаемых в количестве (15). В блоке памяти 1 запоминаются разряды промежуточных слагаемых от 0-го до n-го, в блоке 2 – от n+1 до 2n+1, в блоке i – от (i – 1)n+1 до in+1. Процесс прироста старших ненулевых разрядов будет замедляться (аналогично приросту разрядов счетчика) пропорционально замедлению перехода от этапа i к этапу i+1.
Замечание 2. Если промежуточные ряды сжимать до двухрядного кода, то замедление прироста таково, что время непрерывной потоковой обработки может измеряться месяцами и годами (в зависимости от подбора параметров) при организации всего семи блоков, изображенных на рис. 1 [4, 5]. Время обработки допускает элементарную оценку, на основе которой ограничивается диапазон числовых данных.
Вертикальное потоковое сложение с учетом знаков слагаемых. Предлагается по отдельности суммировать положительные и отрицательные числа входного потока. Когда потребуется знак алгебраической суммы, следует сжать положительные и отрицательные промежуточные ряды до двух, выполнить окончательное сложение в однорядном коде и сложить двоичные коды результатов с учетом знака. Способ должен иметь аналог дополнительного кода (непосредственно дополнительный код использует данные с плавающей точкой). Аналог строится на основе тождества
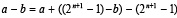 (16)
(16)
с учетом суммы геометрической прогрессии
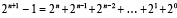 , (17)
, (17)
что в позиционной записи означает
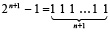 . (18)
. (18)
Из (17), (18) следует, что разность (2n+1 – 1) – b состоит из битовых значений разрядов числа b, преобразованных так, что каждый нулевой бит заменяется битом равным единице, а каждый единичный бит заменяется битом равным нулю (разряды b инвертируются). Результат преобразования определяет обратный код числа b, который ниже обозначается b. Таким образом, b = (2n+1 – 1) – b. Операция a – b выполняется как операция сложения a + b. Чтобы результат перевести в исходный (прямой) код, выполняется коррекция согласно (16):
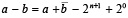 . (19)
. (19)
Правая часть операции (19) означает, что от разряда веса 2n+1 суммы a + b нужно отнять 1, а к разряду веса 20 нужно прибавить 1 (аналог дополнительного кода). Если отрицательные слагаемые появляются только среди чисел вида (1), (2), то описание алгебраического сложения можно считать завершенным. Если же их значение используется в дальнейшей обработке, то коррекция (19) должна относиться не только к разряду фиксированного веса 2n+1: вес старшего разряда может измениться – возрасти или уменьшиться относительно (1), (2), быть переменным для различных шагов обработки. Пусть требуется выполнить алгебраическое сложение положительного и отрицательного числа с весом корректируемого старшего разряда отличным от 2n+1. Очевидно, в преобразованиях (16)–(19) старший разряд может быть как единичным, так и нулевым, схема всегда сохранит правильный результат на выходе операции (19). Поэтому a, b в (16) можно считать имеющими равное число разрядов и одинаковый вес старшего из них. Пусть в данном случае этот вес будет равен 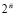 . Тогда алгебраическое сложение повторяет схему (16)–(19) с точностью до замены значения n на значение
. Тогда алгебраическое сложение повторяет схему (16)–(19) с точностью до замены значения n на значение 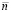 . Проблема заключается в том, что автоматическое кодирование знака суммы выполняется только для операций с плавающей точкой. В случае фиксированной точки требуется априори определить наибольшее по абсолютной величине слагаемое и приписать знак наибольшего по модулю слагаемого результату операции (19). С минимальной временной сложностью это можно сделать следующим образом. Сначала выполняется первая часть операции a – b в виде a + b, где b – обратный код числа b:
. Проблема заключается в том, что автоматическое кодирование знака суммы выполняется только для операций с плавающей точкой. В случае фиксированной точки требуется априори определить наибольшее по абсолютной величине слагаемое и приписать знак наибольшего по модулю слагаемого результату операции (19). С минимальной временной сложностью это можно сделать следующим образом. Сначала выполняется первая часть операции a – b в виде a + b, где b – обратный код числа b: 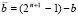 . При этом сложение выполняется поразрядно-параллельно в четыре этапа, содержание которых поясняется на примере. Пусть
. При этом сложение выполняется поразрядно-параллельно в четыре этапа, содержание которых поясняется на примере. Пусть
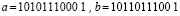 . (20)
. (20)
Тогда 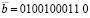 .
.
Этап 1. Выполняется поразрядно-параллельное сложение по вертикали для случая двух слагаемых (N = 2), как описано выше для (1)–(5):
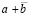 =
= 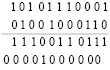 (21)
(21)
Под чертой в (21) – два промежуточных ряда для случая двух входных слагаемых (20).
Этап 2. Два слагаемых промежуточных рядов преобразуются без изменения суммы:
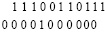 =
=
= 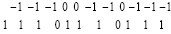 (22)
(22)
В (22) единицы нижнего ряда левой части равенства не преобразуются, а каждая единица верхнего ряда преобразуется как 1 = 2 – 1. При этом –1 остается в верхнем ряду вместо 1 того же разряда, а 2 записывается как 1 разряда веса на один большего, чем преобразуемая 1 верхнего ряда, с соответственным смещением справа налево, сверху вниз – в нижний ряд. Это всегда возможно: после этапа 1 в смещенном по диагонали от единицы разряде нижнего ряда априори содержится значение 0. Если бы в смещенном от 1 верхнего ряда по диагонали разряде нижнего ряда оказалось число 1, это означало бы, что сумма бит по вертикали равна 11 = 3, тогда как складывались только два двоичных коэффициента равного веса.
Этап 3. По всем разрядам правой части (22) снова выполняется сложение по вертикали. Получится
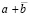 =
=
=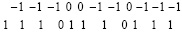 =
=
= 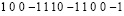 . (23)
. (23)
Этап 4. Наличие –1 в девятом справа налево (при отсчете от единицы) разряде в правой части цепочки равенств (23) обусловлено тем, что в нижнем промежуточном ряду коэффициент этого веса равнялся нулю (вообще появление –1 на выходе (23) возможно тогда и только тогда, когда на входе по вертикали под –1 расположен 0). Рассматриваемое значение –1 имеет наибольший вес среди других значений –1, потому что все коэффициенты большего веса нижнего ряда на входе (23) были единицами (это общий признак значения –1 наибольшего веса). Наличие таких единиц нижнего ряда единственным образом соответствует наличию нулей на их местах в левой части (22). В свою очередь, такие нули старших разрядов нижнего ряда появились в результате формирования промежуточных рядов на этапе 1, когда сложение выполнялось только по вертикали, двоичная сумма вертикального среза записывалась справа налево по диагонали от разряда верхнего к разряду нижнего ряда. Сумма значений данных разрядов была единичной по той и только той причине, что складываемые биты 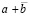 всегда были один нулем, а другой единицей. С учетом того, что
всегда были один нулем, а другой единицей. С учетом того, что 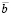 представлено в обратном коде, это означает, что рассматриваемые старшие разряды (слева от –1 наибольшего веса) a и b содержали равные друг другу значения. Нетрудно видеть, что данные рассуждения воспроизводятся в общем случае и имеет место
представлено в обратном коде, это означает, что рассматриваемые старшие разряды (слева от –1 наибольшего веса) a и b содержали равные друг другу значения. Нетрудно видеть, что данные рассуждения воспроизводятся в общем случае и имеет место
Лемма 1. Если значения i – 1 всех старших разрядов a и b совпадают, а в i-м слева направо разряде различаются, то после выполнения этапов 1–3 в i-м разряде однорядной суммы 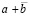 с необходимостью окажется значение –1.
с необходимостью окажется значение –1.
Следствие 2. Если в условиях леммы 1 ни одно значение разряда однорядной суммы 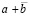 не равно –1, то a = b.
не равно –1, то a = b.
На рассматриваемом (4-м) этапе необходимо выделить значение –1 наибольшего веса среди других значений –1 однорядной суммы 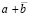 . Это можно сделать схемотехнически: из каждого разряда в случае его значения равного –1 подается сигнал запрета выходного значения одновременно на все младшие разряды. Для этого необходимы фиксированные линии связи для приема рассматриваемых сигналов в каждом разряде. Задержка распространения сигнала запрета формально может оцениваться как единичная.
. Это можно сделать схемотехнически: из каждого разряда в случае его значения равного –1 подается сигнал запрета выходного значения одновременно на все младшие разряды. Для этого необходимы фиксированные линии связи для приема рассматриваемых сигналов в каждом разряде. Задержка распространения сигнала запрета формально может оцениваться как единичная.
Пусть выделено значение –1 в разряде наибольшего веса с номером i (в нумерации от 0 слева направо). Вес разряда равен 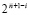 (при нумерации справа налево номер разряда
(при нумерации справа налево номер разряда 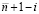 ). Остается сравнить значения разрядов с тем же номером i уменьшаемого a и вычитаемого b. Большее значение определяет знак разности a – b. Здесь учитывается, что
). Остается сравнить значения разрядов с тем же номером i уменьшаемого a и вычитаемого b. Большее значение определяет знак разности a – b. Здесь учитывается, что 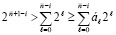 при любых значениях бит
при любых значениях бит 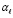 ,
, 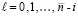 .
.
С учетом поразрядной параллельности рассмотренных операций имеет место
Лемма 2. Задержка идентификации знака разности a – b в результате выполнения этапов 1–4 формально не зависит от числа разрядов a и b, при этом измеряется длительностью t = O(1).
В [6, 7] обсуждаются алгоритмические схемы выделения старшего ненулевого разряда двух сравниваемых чисел с задержкой 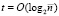 .
.
О распространении поразрядно-параллельной потоковой обработки на разновидности групповых арифметических операций. Изложенный метод распространяется на умножение, при этом в роли группы слагаемых на входе выступает школьная схема умножения, результат вертикальной обработки – набор промежуточных рядов [1]. Умножение на текущий сомножитель выполняется по дистрибутивности на такой набор промежуточных слагаемых. Количество промежуточных рядов, как и в случае потока слагаемых, ограничено при неограниченном потоке сомножителей. Для вычисления произведения последовательности сомножителей 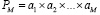 в [1] приводится оценка числа промежуточных рядов
в [1] приводится оценка числа промежуточных рядов
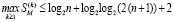 , (24)
, (24)
где количество разрядов сомножителей равно n + 1, M произвольно. Проблема возникает, если меняется алгоритм умножения, например если вычисляется 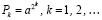 В этом случае для ограничения числа промежуточных рядов приходится ограничить число разрядов таких рядов на выходе каждого шага умножения [1]. Для простой последовательности умножений с оценкой (24) схема умножения с промежуточными рядами громоздка, однако их количество можно уменьшить до двух. С аналогичными издержками метод переносится на алгоритмы умножения со сложением, например на схему Горнера вычисления полинома, на умножение матриц, на выполнение итерационных методов линейной алгебры [8] и т.д. Для практической реализации приемлема модификация метода, описываемая ниже (в дальнейшем она иллюстрируется также применительно к умножению).
В этом случае для ограничения числа промежуточных рядов приходится ограничить число разрядов таких рядов на выходе каждого шага умножения [1]. Для простой последовательности умножений с оценкой (24) схема умножения с промежуточными рядами громоздка, однако их количество можно уменьшить до двух. С аналогичными издержками метод переносится на алгоритмы умножения со сложением, например на схему Горнера вычисления полинома, на умножение матриц, на выполнение итерационных методов линейной алгебры [8] и т.д. Для практической реализации приемлема модификация метода, описываемая ниже (в дальнейшем она иллюстрируется также применительно к умножению).
Сжатие промежуточных рядов до двух слагаемых при потоковой обработке. Пусть рассматривается обработка потока (1) в условиях теоремы 1. Выполняется следующая модификация метода. Сумма (1) вычисляется посредством основного алгоритма теоремы 1, соответственного (10), но при этом 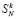 промежуточных рядов на шаге k не сразу подсоединяются к входному набору из N новых слагаемых для шага k + 1, а только после того, как над этими промежуточными рядами выполнится операция однократного сжатия. Однократное сжатие выполняется так, как если бы эти промежуточные ряды представляли собой входной набор слагаемых, без изменения способа, описанного в теореме 1. Иными словами, над этим набором промежуточных рядов выполняется операция поразрядно-параллельного сложения без вычисления переноса. Результатом однократного сжатия будет новый (сжатый) набор промежуточных рядов. Именно этот сжатый набор рядов подсоединяется к входному набору из N новых слагаемых для шага k + 1 основного алгоритма. На шаге 1 модифицированного таким образом основного алгоритма после однократного сжатия набор будет состоять из
промежуточных рядов на шаге k не сразу подсоединяются к входному набору из N новых слагаемых для шага k + 1, а только после того, как над этими промежуточными рядами выполнится операция однократного сжатия. Однократное сжатие выполняется так, как если бы эти промежуточные ряды представляли собой входной набор слагаемых, без изменения способа, описанного в теореме 1. Иными словами, над этим набором промежуточных рядов выполняется операция поразрядно-параллельного сложения без вычисления переноса. Результатом однократного сжатия будет новый (сжатый) набор промежуточных рядов. Именно этот сжатый набор рядов подсоединяется к входному набору из N новых слагаемых для шага k + 1 основного алгоритма. На шаге 1 модифицированного таким образом основного алгоритма после однократного сжатия набор будет состоять из 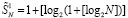 промежуточных рядов.
промежуточных рядов.
На шаге 2 основного алгоритма после однократного сжатия
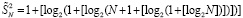 .
.
На шаге k после однократного сжатия получится (25)
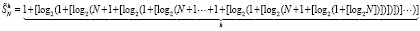 .
.
Из (25)
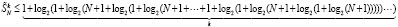 . (26)
. (26)
С учетом того, что при использовании однократного сжатия число промежуточных рядов не больше чем в исходном методе, можно оценить это число на всех предшествующих шагах сверху из (14). На двух последних шагах используются начальные члены (26). В результате
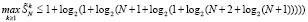
или
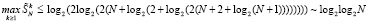 . (27)
. (27)
Точное число промежуточных рядов для любого N можно рассчитать из (25). Аналогично, можно рассматривать двукратное сжатие на каждом шаге основного алгоритма и при этом для оценки числа промежуточных рядов использовать (27). Нетрудно видеть, что это число оценивается как 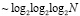 . Общий вариант основного алгоритма с m-кратным сжатием промежуточных рядов при достаточном значении m приводит всего к двум промежуточным рядам на выходе каждого шага, что является практически приемлемым вариантом организации поразрядно-параллельной обработки без вычисления переноса. Издержка такой модификации состоит в m-кратном замедлении обработки по сравнению с исходным вариантом алгоритма. Легко оценить число шагов m сжатия для любого конкретного N. Например, если N = 1024, то после первичной обработки входного набора число промежуточных рядов равно
. Общий вариант основного алгоритма с m-кратным сжатием промежуточных рядов при достаточном значении m приводит всего к двум промежуточным рядам на выходе каждого шага, что является практически приемлемым вариантом организации поразрядно-параллельной обработки без вычисления переноса. Издержка такой модификации состоит в m-кратном замедлении обработки по сравнению с исходным вариантом алгоритма. Легко оценить число шагов m сжатия для любого конкретного N. Например, если N = 1024, то после первичной обработки входного набора число промежуточных рядов равно 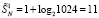 . При первом сжатии промежуточных рядов их количество сократится до
. При первом сжатии промежуточных рядов их количество сократится до 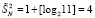 . Еще одно сжатие влечет
. Еще одно сжатие влечет 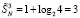 . Третье сжатие приводит к двум промежуточным рядам:
. Третье сжатие приводит к двум промежуточным рядам: 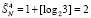 . Число шагов m-кратного сжатия в данном случае m = 3. Сокращение количества промежуточных рядов с 11 до 2 за три шага, менее трудоемких чем первичная обработка входного набора из N = 1024 слагаемых, практически целесообразно. Если такое сжатие выполнять при обработке каждого входного набора, то вся обработка без прерывания потока данных будет производиться в двухрядном коде. С такой модификацией метод переносится на умножение и другие арифметические операции, позволяя выполнять их в потоке, поразрядно-параллельно и без вычисления переноса. Вместе с тем возможно поразрядно-параллельное сжатие двухрядного кода в однорядный.
. Число шагов m-кратного сжатия в данном случае m = 3. Сокращение количества промежуточных рядов с 11 до 2 за три шага, менее трудоемких чем первичная обработка входного набора из N = 1024 слагаемых, практически целесообразно. Если такое сжатие выполнять при обработке каждого входного набора, то вся обработка без прерывания потока данных будет производиться в двухрядном коде. С такой модификацией метод переносится на умножение и другие арифметические операции, позволяя выполнять их в потоке, поразрядно-параллельно и без вычисления переноса. Вместе с тем возможно поразрядно-параллельное сжатие двухрядного кода в однорядный.
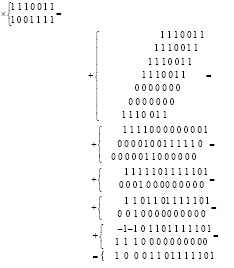
Поразрядно-параллельное сложение двоичных полиномов без вычисления переноса. Пусть нужно сложить два двоичных числа вида (2), (3). Предлагаемый способ поясняется на примере нахождения суммы
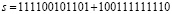 . (28)
. (28)
Первое из слагаемых (28) располагается в первой сверху строке, второе – во второй, над чертой, разряд под разрядом равного веса:
|
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
Шаг 1. Под чертой поразрядно-параллельно формируются суммы коэффициентов, расположенных по вертикали над чертой, в каждой паре разрядов равного веса. Сумма каждых двух таких бит записывается в позиционном двоичном коде со смещением по диагонали справа налево, сверху вниз согласно весу коэффициента. Этот шаг – частный случай обработки потока (1) при N = 2. Такая операция описана в (5), (6) для случая N = 4. Эта же операция применялась в (21) на этапе 1 для случая N = 2 с целью формирования знака разности. В результате выполнения шага 1 все потенциальные переносы в двух полученных промежуточных рядах с необходимостью образуют цепочки специального вида. Именно, в верхнем промежуточном ряду в цепочке переноса располагаются единицы без пропуска, в нижнем ряду, под единицей младшего в цепочке веса, также располагается единица (единица переноса), под остальными единицами верхнего ряда цепочки в нижнем ряду единице переноса необходимо предшествуют нули:
 (29)
(29)
При этом ближайшие друг к другу цепочки переноса вида (29) всегда взаимно отделены вертикальной парой промежуточных нулей:
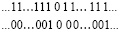 (30)
(30)
Лемма 3. Каковы бы ни были два складываемых двоичных полинома, на выходе шага 1 любая цепочка переноса в промежуточных рядах имеет вид (29), где в цепочке верхнего ряда не меньше одной единицы. При этом любые две соседние цепочки переносов, аналогично (30), необходимо отделены друг от друга хотя бы одной вертикальной парой нулей (парой нулевых двоичных коэффициентов равного веса).
Доказательство. Если вместо хотя бы одного нуля в (29) оказалась единица, это означало бы запись по диагонали справа налево, сверху вниз двоичного числа 11 = 3, являющегося суммой двух бит равного веса, что невозможно: по вертикали складывались два двоичных коэффициента одинакового веса, их сумма либо 01 = 1, либо 10 = 2. Далее, если бы между двумя ближайшими друг к другу цепочками переносов вида (30) на месте любого нуля вертикальной пары нулевых коэффициентов равного веса оказалась единица, это, как и в только что рассмотренном случае, влекло бы запись по диагонали справа налево, сверху вниз суммы двух бит (двоичных коэффициентов равного веса) 11 = 3, что невозможно. Лемма доказана.
Из леммы 3 следует, что после шага 1 никакие переносы и цепочки переносов не могут накладываться друг на друга, поэтому их все можно выполнить взаимно независимо и параллельно.
Шаг 2. Каждая двухрядная цепочка вида (29) преобразуется в однорядную цепочку, представляющую собой результат выполнения переноса
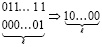 . (31)
. (31)
В левой части (31) слева от цепочки единиц необходимая вертикальная пара нулей  , отделяющая цепочку переноса от соседней слева цепочки переноса или от ближайшей слева 1, не принадлежащей какой-либо цепочке переноса. Преобразование (31) выполняется с помощью схемы из логических и разрядных элементов (рис. 2). Здесь и ниже под разрядным элементом понимается простейший процессорный или, возможно, логический элемент, реализующий рассматриваемые преобразования вертикальной пары бит равного веса в фиксированном разряде двухрядного кода, полученного на выходе шага 1. В предлагаемой схеме разрядный элемент младшего разряда двухрядного кода левой части (31) при наличии вертикальной пары
, отделяющая цепочку переноса от соседней слева цепочки переноса или от ближайшей слева 1, не принадлежащей какой-либо цепочке переноса. Преобразование (31) выполняется с помощью схемы из логических и разрядных элементов (рис. 2). Здесь и ниже под разрядным элементом понимается простейший процессорный или, возможно, логический элемент, реализующий рассматриваемые преобразования вертикальной пары бит равного веса в фиксированном разряде двухрядного кода, полученного на выходе шага 1. В предлагаемой схеме разрядный элемент младшего разряда двухрядного кода левой части (31) при наличии вертикальной пары  , и только в этом случае инициирует работу разрешающей параллельной схемы элементов & путем параллельной подачи значения 1 на вход каждого элемента &. Каждый из элементов & разрешающей схемы помимо прямого входа имеет инверсный вход. На инверсный вход элемента & по фиксированной прямой линии связи с разрядным элементом, после сигнала разрешения на преобразование разряда, этот разрядный элемент будет посылать значение разряда из верхнего ряда соответственной ему вертикальной пары коэффициентов равного веса. Прямая линия связи между разрядным элементом и элементом & разрешающей схемы является единственной для каждого разряда двухрядного кода и для каждого элемента & разрешающей схемы. Иными словами, все разрядные элементы и элементы разрешающей параллельной схемы находятся во взаимно однозначном соответствии, реализуемом (рис. 2) фиксированными прямыми линиями связи. В силу соответствия количество элементов & разрешающей схемы равно числу старших разрядов двухрядного кода в отсчете от пары
, и только в этом случае инициирует работу разрешающей параллельной схемы элементов & путем параллельной подачи значения 1 на вход каждого элемента &. Каждый из элементов & разрешающей схемы помимо прямого входа имеет инверсный вход. На инверсный вход элемента & по фиксированной прямой линии связи с разрядным элементом, после сигнала разрешения на преобразование разряда, этот разрядный элемент будет посылать значение разряда из верхнего ряда соответственной ему вертикальной пары коэффициентов равного веса. Прямая линия связи между разрядным элементом и элементом & разрешающей схемы является единственной для каждого разряда двухрядного кода и для каждого элемента & разрешающей схемы. Иными словами, все разрядные элементы и элементы разрешающей параллельной схемы находятся во взаимно однозначном соответствии, реализуемом (рис. 2) фиксированными прямыми линиями связи. В силу соответствия количество элементов & разрешающей схемы равно числу старших разрядов двухрядного кода в отсчете от пары  (на рис. 2 не отражены элементы разрешающих схем старших и младших относительно пары
(на рис. 2 не отражены элементы разрешающих схем старших и младших относительно пары  разрядов). С выхода каждого элемента & идет фиксированная обратная линия связи в тот же соответственный разрядный элемент, из которого выходит прямая линия связи. Геометрически прямая и обратная линия связи параллельны друг другу. Каждый элемент & разрешающей схемы имеет взаимно однозначно сопоставленный ему (рядом расположенный) дополнительный элемент с собственными входами и выходами. Этот дополнительный к & элемент также имеет фиксированные прямую и обратную линии связи с тем же разрядным элементом, с которым имеет взаимно однозначное соответствие и линии связи элемент &, геометрически те и другие линии связи параллельны друг другу. Дополнительные элементы и их линии связи не отображены на рис. 2. Дополнительные элементы разрешающей схемы подают сигнал разрешения обработки на сопоставленные разрядные элементы после того, как на их входы поступят значения вертикальной пары разрядов из этих разрядных элементов и они обработают эти значения.
разрядов). С выхода каждого элемента & идет фиксированная обратная линия связи в тот же соответственный разрядный элемент, из которого выходит прямая линия связи. Геометрически прямая и обратная линия связи параллельны друг другу. Каждый элемент & разрешающей схемы имеет взаимно однозначно сопоставленный ему (рядом расположенный) дополнительный элемент с собственными входами и выходами. Этот дополнительный к & элемент также имеет фиксированные прямую и обратную линии связи с тем же разрядным элементом, с которым имеет взаимно однозначное соответствие и линии связи элемент &, геометрически те и другие линии связи параллельны друг другу. Дополнительные элементы и их линии связи не отображены на рис. 2. Дополнительные элементы разрешающей схемы подают сигнал разрешения обработки на сопоставленные разрядные элементы после того, как на их входы поступят значения вертикальной пары разрядов из этих разрядных элементов и они обработают эти значения.
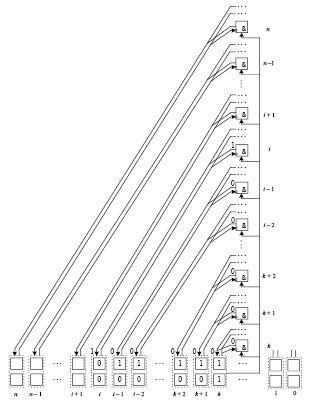
Рис. 2. Поразрядно-параллельное преобразование цепочки переноса
Если на вход дополнительного элемента поступает сигнал из разрядного элемента с парой  (и только в этом случае), то он интерпретируется как отмена сигнала разрешения на обработку разрядных значений для всех тех разрядных элементов, которые сопоставлены элементам разрешающей параллельной схемы, расположенным выше элемента &, соответственного данному дополнительному элементу (получившему сигнал
(и только в этом случае), то он интерпретируется как отмена сигнала разрешения на обработку разрядных значений для всех тех разрядных элементов, которые сопоставлены элементам разрешающей параллельной схемы, расположенным выше элемента &, соответственного данному дополнительному элементу (получившему сигнал  ). Отмена сигнала разрешения параллельно подается на все дополнительные элементы, элементы & которых расположены выше элемента &, получившего сигнал
). Отмена сигнала разрешения параллельно подается на все дополнительные элементы, элементы & которых расположены выше элемента &, получившего сигнал  , что исключает поступление от них на входы всех сопоставленных им разрядных элементов сигнала разрешения обработки разрядных значений (находящихся за пределами данной цепочки переноса). Термины «разрешение» и «отмена разрешения» сохраняются ниже. При этом они понимаются именно как сигналы разрешения и соответственно его отсутствия для разрядных элементов на преобразование значений разрядов. Выдающие (через дополнительные элементы) разрешение на обработку элементы & будут именоваться разрешающими. Несмотря на то, что отмена сигнала разрешения может поступать из различных разрядов, предшествующих слева преобразуемой цепочке переноса, единственным разрешающим элементом &, на дополнительный элемент к которому поступил сигнал от пары
, что исключает поступление от них на входы всех сопоставленных им разрядных элементов сигнала разрешения обработки разрядных значений (находящихся за пределами данной цепочки переноса). Термины «разрешение» и «отмена разрешения» сохраняются ниже. При этом они понимаются именно как сигналы разрешения и соответственно его отсутствия для разрядных элементов на преобразование значений разрядов. Выдающие (через дополнительные элементы) разрешение на обработку элементы & будут именоваться разрешающими. Несмотря на то, что отмена сигнала разрешения может поступать из различных разрядов, предшествующих слева преобразуемой цепочке переноса, единственным разрешающим элементом &, на дополнительный элемент к которому поступил сигнал от пары  , окажется нижний среди всех таких элементов, а именно тот, который соответствует паре
, окажется нижний среди всех таких элементов, а именно тот, который соответствует паре  , ограничивающей слева преобразуемую цепочку из (31). Отличные от
, ограничивающей слева преобразуемую цепочку из (31). Отличные от  комбинации бит, поступающие на входы дополнительных элементов, не интерпретируются как отмена сигнала разрешения. Поэтому разрешающими останутся все элементы & параллельной схемы, расположенные ниже соответственного паре
комбинации бит, поступающие на входы дополнительных элементов, не интерпретируются как отмена сигнала разрешения. Поэтому разрешающими останутся все элементы & параллельной схемы, расположенные ниже соответственного паре  элемента &, а также собственно элемент &, соответственный этой паре. Иными словами, разрешающими останутся те и только те элементы & параллельной схемы, которые находятся во взаимно однозначном соответствии с разрядными элементами преобразуемой цепочки переноса (и только в случае его наличия, то есть в случае инициации разрешающей параллельной схемы).
элемента &, а также собственно элемент &, соответственный этой паре. Иными словами, разрешающими останутся те и только те элементы & параллельной схемы, которые находятся во взаимно однозначном соответствии с разрядными элементами преобразуемой цепочки переноса (и только в случае его наличия, то есть в случае инициации разрешающей параллельной схемы).
Поскольку все цепочки переноса взаимно отделены, то в силу взаимно однозначного соответствия разрядных и разрешающих элементов геометрически (пространственно) взаимно отделенными оказываются все разрешающие элементы & инициированных параллельных схем вместе с соответственными им разрядными элементами. Все такие схемы могут работать взаимно независимо, параллельно и синхронно реализовать переносы в своих цепочках.
Линия связи, которая идет от разрядного элемента пары  , продолжается на все элементы & (аналогично, на дополнительные к ним элементы) разрешающих параллельных схем, сопоставленных всем младшим разрядам рассматриваемого двухрядного кода. При этом разрешающим на ней может быть один и только один элемент &, именно тот, который находится на ее пересечении с инициированной парой
, продолжается на все элементы & (аналогично, на дополнительные к ним элементы) разрешающих параллельных схем, сопоставленных всем младшим разрядам рассматриваемого двухрядного кода. При этом разрешающим на ней может быть один и только один элемент &, именно тот, который находится на ее пересечении с инициированной парой  разрешающей параллельной схемой элементов &. В самом деле, переносы из младших относительно пары
разрешающей параллельной схемой элементов &. В самом деле, переносы из младших относительно пары  разрядов отделены от этой пары справа вертикальной парой
разрядов отделены от этой пары справа вертикальной парой  . Все линии связи цепочек этих переносов расположены ниже линий связи элементов рассматриваемой разрешающей параллельной схемы. Они не достигают разрядов преобразуемой цепочки переноса, в частности не достигнут рассматриваемой пары
. Все линии связи цепочек этих переносов расположены ниже линий связи элементов рассматриваемой разрешающей параллельной схемы. Они не достигают разрядов преобразуемой цепочки переноса, в частности не достигнут рассматриваемой пары  . С другой стороны, все элементы разрешающих параллельных схем &, расположенные выше преобразований переноса младших относительно пары
. С другой стороны, все элементы разрешающих параллельных схем &, расположенные выше преобразований переноса младших относительно пары  разрядов, но не выше рассматриваемой линии связи, которая идет от разрядного элемента пары
разрядов, но не выше рассматриваемой линии связи, которая идет от разрядного элемента пары  (ограничивающей слева цепочку переноса), инициированы как разрешающие разрядные преобразования. Они также являются единственными разрешающими элементами & на своих линиях связи. Иначе бы другие элементы на их линиях связи разрешали бы перенос в рассматриваемую цепочку. Это невозможно вследствие взаимной отделенности переносов и взаимно однозначного соответствия реализующих их разрядных элементов линиям связи и инициированным элементам разрешающих параллельных схем. Разрядные элементы старших относительно пары
(ограничивающей слева цепочку переноса), инициированы как разрешающие разрядные преобразования. Они также являются единственными разрешающими элементами & на своих линиях связи. Иначе бы другие элементы на их линиях связи разрешали бы перенос в рассматриваемую цепочку. Это невозможно вследствие взаимной отделенности переносов и взаимно однозначного соответствия реализующих их разрядных элементов линиям связи и инициированным элементам разрешающих параллельных схем. Разрядные элементы старших относительно пары  (ограничивающей слева рассматриваемую цепочку переноса) разрядов свои переносы (при их наличии) реализуют инициацией расположенных слева от данной пары
(ограничивающей слева рассматриваемую цепочку переноса) разрядов свои переносы (при их наличии) реализуют инициацией расположенных слева от данной пары  разрешающих параллельных схем, никак не связанных с рассматриваемой линией связи. В результате рассматриваемая линия связи, по которой поступает сигнал от пары
разрешающих параллельных схем, никак не связанных с рассматриваемой линией связи. В результате рассматриваемая линия связи, по которой поступает сигнал от пары  , содержит единственный разрешающий элемент параллельной схемы &, причем только при наличии переноса. Кроме того, каждая линия связи, которой принадлежит элемент & разрешающей параллельной схемы, может содержать только один разрешающий элемент & (также только при наличии переноса). Это именно тот элемент, который находится на ее пересечении с инициированной разрешающей параллельной схемой.
, содержит единственный разрешающий элемент параллельной схемы &, причем только при наличии переноса. Кроме того, каждая линия связи, которой принадлежит элемент & разрешающей параллельной схемы, может содержать только один разрешающий элемент & (также только при наличии переноса). Это именно тот элемент, который находится на ее пересечении с инициированной разрешающей параллельной схемой.
В результате разрешающими являются те и только те элементы & инициированной параллельной схемы, которые находятся во взаимно однозначном соответствии с разрядными элементами преобразуемой цепочки переноса. При этом все инициированные параллельные схемы с разрешающими элементами & и соответствующими им линиями связи не пересекаются друг с другом в том смысле, что по каждой линии связи в разрядный элемент может идти только один разрешающий сигнал, и только если разрядный элемент принадлежит цепочке переноса.
Замечание 3. На одной линии связи инициированным может оказаться только один сигнал разрешения, но контактные элементы на этой линии соответствуют и всем значениям отмены разрешения. Инициированный сигнал поступит в сопоставленный разрядный элемент как значение многовходовой логической схемы Ѵ из контактных элементов.
При помощи описанных схем операции шага 2 выполняются следующим образом. На соответственные разрядные элементы от разрешающих элементов & (через дополнительные к ним элементы) параллельно поступают сигналы разрешения преобразования. После разрешения разрядные элементы параллельно подают из своих вертикальных пар значения разрядов верхнего ряда на инверсные входы элементов &. Если на инверсные входы элементов & из разрядов верхнего ряда поступают значения 1, то по обратным линиям связи в эти же разряды поступят значения 0 (рис. 2). Разрядные элементы запишут поступившие новые значения на место исходных. Тогда во всех данных разрядах оказывается значение 0. На инверсный вход верхнего разрешающего элемента & поступает значение 0 старшего разряда верхнего ряда преобразования (31) (от вертикальной пары  ). Поэтому по обратной линии связи в этот разряд поступит значение 1. Соответственный разрядный элемент запишет это значение на место исходного. В итоге полностью реализуется преобразование (31). Результат преобразования располагается в верхнем ряду двухрядного кода. Все аналогичные преобразования цепочек переноса не зависят друг от друга и будут выполнены одновременно (параллельно) с рассмотренным преобразованием. Те значения разрядов, которые не входили в цепочки переносов, останутся неизменными, поскольку на входы их разрядных элементов не поступал сигнал разрешения преобразования. На выходе шага 2 будет полностью реализовано сложение в прямом коде пары двоичных полиномов вида (2). Из изложенного вытекает
). Поэтому по обратной линии связи в этот разряд поступит значение 1. Соответственный разрядный элемент запишет это значение на место исходного. В итоге полностью реализуется преобразование (31). Результат преобразования располагается в верхнем ряду двухрядного кода. Все аналогичные преобразования цепочек переноса не зависят друг от друга и будут выполнены одновременно (параллельно) с рассмотренным преобразованием. Те значения разрядов, которые не входили в цепочки переносов, останутся неизменными, поскольку на входы их разрядных элементов не поступал сигнал разрешения преобразования. На выходе шага 2 будет полностью реализовано сложение в прямом коде пары двоичных полиномов вида (2). Из изложенного вытекает
Лемма 4. Результат выполнения шагов 1, 2 всегда располагается в один ряд (верхний ряд двух промежуточных рядов), то есть имеет вид однорядного прямого кода суммы двух двоичных полиномов вида (2), (3).
Описанная схема допускает видоизменение, при котором для разрядных элементов упрощается разрешение на обработку, но в этом случае они самостоятельно выполняют два дополнительных шага. Пусть каждый элемент & разрешающей параллельной схемы обладает не инверсным, а прямым входом. По-прежнему каждому из этих элементов сопоставляется один дополнительный элемент с ранее описанными линиями связи. Пусть парой  инициирована разрешающая параллельная схема элементов &. Из разрядного элемента, соответственного вертикальной паре
инициирована разрешающая параллельная схема элементов &. Из разрядного элемента, соответственного вертикальной паре  , ограничивающей слева данную цепочку переноса, по прямой линии связи на вход дополнительного к соответственному элементу & подается нулевое значение. Дополнительный элемент параллельно распространяет нулевое значение как сигнал отмены разрешения на все расположенные выше элементы &, а также на соответственный ему самому элемент &. Одновременно, по прямым линиям связи на входы элементов & инициированной разрешающей схемы подаются единичные значения разрядов верхнего ряда, полученного на выходе шага 1. По обратным линиям связи в разрядные элементы, соответственные преобразуемой цепочке переноса, поступят единичные значения. Эти значения разрядные элементы интерпретируют как сигналы разрешения на два дополнительных шага обработки. В результате разрешающие сигналы получат разрядные элементы только с единичными разрядами верхнего ряда преобразуемой цепочки переноса (и только в случае его наличия). Аналогичные схемы любых других разрядов взаимно отделены по описанным прежде соображениям. Два дополнительных шага состоят в следующем. Разрядный элемент, основываясь на тождестве 1 = 2 – 1, меняет знак 1 разряда верхнего ряда (31) на противоположный: –1. Одновременно он записывает (по диагонали) в разряд на единицу большего веса в нижний ряд значение 1. При этом исходные значения 1 разрядов нижнего ряда, а также значения 1 и 0 верхнего ряда, не принадлежащие цепочкам переноса (на них не может поступить разрешающий преобразование сигнал), не подвергаются никакому преобразованию и сохраняются без изменений. Затем по вертикали разрядные элементы параллельно складывают коэффициенты равного веса в каждом разряде. Для цепочки (31) получится
, ограничивающей слева данную цепочку переноса, по прямой линии связи на вход дополнительного к соответственному элементу & подается нулевое значение. Дополнительный элемент параллельно распространяет нулевое значение как сигнал отмены разрешения на все расположенные выше элементы &, а также на соответственный ему самому элемент &. Одновременно, по прямым линиям связи на входы элементов & инициированной разрешающей схемы подаются единичные значения разрядов верхнего ряда, полученного на выходе шага 1. По обратным линиям связи в разрядные элементы, соответственные преобразуемой цепочке переноса, поступят единичные значения. Эти значения разрядные элементы интерпретируют как сигналы разрешения на два дополнительных шага обработки. В результате разрешающие сигналы получат разрядные элементы только с единичными разрядами верхнего ряда преобразуемой цепочки переноса (и только в случае его наличия). Аналогичные схемы любых других разрядов взаимно отделены по описанным прежде соображениям. Два дополнительных шага состоят в следующем. Разрядный элемент, основываясь на тождестве 1 = 2 – 1, меняет знак 1 разряда верхнего ряда (31) на противоположный: –1. Одновременно он записывает (по диагонали) в разряд на единицу большего веса в нижний ряд значение 1. При этом исходные значения 1 разрядов нижнего ряда, а также значения 1 и 0 верхнего ряда, не принадлежащие цепочкам переноса (на них не может поступить разрешающий преобразование сигнал), не подвергаются никакому преобразованию и сохраняются без изменений. Затем по вертикали разрядные элементы параллельно складывают коэффициенты равного веса в каждом разряде. Для цепочки (31) получится
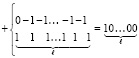 . (32)
. (32)
В данном приложении в младшем разряде на выходе рассматриваемого преобразования всегда будет 0 в силу наличия в нем сдвоенных единиц  до начала преобразования, что отличает приложение данного преобразования от приложений в (21)–(23). Для примера (28) на выходе шага 1 получался двухрядный код с тремя цепочками переноса, этот код располагается над чертой:
до начала преобразования, что отличает приложение данного преобразования от приложений в (21)–(23). Для примера (28) на выходе шага 1 получался двухрядный код с тремя цепочками переноса, этот код располагается над чертой:
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
-1 |
-1 |
0 |
-1 |
-1 |
0 |
-1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
Под чертой располагается тождественное преобразование этого кода, производимое разрядными элементами в каждом разряде (вне цепочек переноса, а также в единичных разрядах нижнего ряда данное преобразование не выполняется). Остается параллельно по всем разрядам сложить по вертикали коэффициенты равного веса, чтобы получить окончательное значение однорядного прямого кода суммы слагаемых (28).
|
0 |
0 |
-1 |
-1 |
0 |
-1 |
-1 |
0 |
-1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
Окончательный прямой код суммы (28) расположен под чертой.
Метод не меняется, если одно слагаемое дано в прямом коде, другое – в обратном. Тем самым он переносится на операцию вычитания. Однако определение знака разности сохраняет описанную ранее специфику.
Оценка и понижение сложности поразрядно-параллельного сумматора. Описанный на шагах 1, 2 сумматор двух чисел вида (2), (3) содержит n + 1 разрядных элементов, фактически представляющих собой логические элементы сравнительно небольшой сложности. Каждому разрядному элементу сопоставлен элемент & разрешающей параллельной схемы и дополнительный к нему элемент. На разряд с номером i (отсчет справа налево), i = 0,1,2,…n, приходится n – i + 1 элементов & (рис. 2) и такое же количество дополнительных к ним элементов. В сумме количество 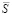 элементов (сложность) сумматора составит
элементов (сложность) сумматора составит
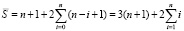 ,
,
или
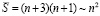 . (33)
. (33)
Временная сложность t (время сложения) сумматора, измеряемая числом последовательных шагов его работы, определяется шагами 1, 2 (без модификации), длительность каждого из которых сопоставима с длительностью τ переключения элемента. Отсюда время сложения двух n + 1-разрядных двоичных полиномов определяется как
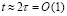 , (34)
, (34)
где t формально не зависит от числа разрядов. Из изложенного вытекает
Теорема 2. Поразрядно-параллельное сложение двух (n + 1)-разрядных двоичных чисел вида (2), (3), выполняемое по шагам 1, 2, не использует вычисление переноса, выполняется с временной сложностью (34), не зависящей от числа разрядов n + 1. При этом количество элементов (сложность) сумматора оценивается из (33).
Замечание 4. Если в условиях теоремы 2 используется видоизменение схемы на основе преобразования (32), то утверждение теоремы сохранится с оговоркой, что коэффициент оценки (34) увеличится примерно вдвое.
Квадратичное количество элементов сумматора влечет принципиальную трудность при неограниченном росте числа разрядов слагаемых. Непосредственно ниже обсуждается возможность снижения его сложности за счет увеличения числа шагов работы. Пусть n + 1 является целой степенью по основанию 2, пусть выбрано число q, также равное целой степени по основанию 2, причем q < n + 1. Предлагается все разряды слагаемых в порядке расположения разделить на q групп по (n + 1) / q разрядов. Параллельно по всем q группам, в каждой группе выполняются оба шага поразрядно-параллельного сложения так, как если бы складывались два (n + 1)/q-разрядных числа без какой-либо связи с другими группами. При этом первый шаг вертикального сложения бит равного веса выполняется так, как если бы не было разделения на группы. В частности, для записи суммы бит равного веса старших разрядов группы используется младший разряд соседней группы второго ряда промежуточных рядов. В результате все переносы окажутся взаимно отделенными независимо от принадлежности к группам. С учетом (33) для данных двух шагов достаточно, чтобы схема на рис. 2 (она должна включать не отображенные на рисунке элементы), адаптированная к каждой отдельной группе, содержала 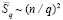 элементов. В сумме по всем q группам количество элементов составит
элементов. В сумме по всем q группам количество элементов составит
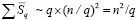 . (35)
. (35)
Преобразования одновременно во всех группах будут выполнены за время (34). Все переносы внутри каждой группы, а также транзитные между группами, взаимно отделены парами вертикальных нулей, на втором шаге они взаимно независимо реализуются во всех отдельных группах. По окончании сложения в группах требуется выполнить каждый перенос (если таковой возникнет) из одной группы в другую. Такой перенос возникает, когда правая часть двухрядной цепочки из (31) оказывается справа от общей границы соседних групп, а левая – слева от этой границы. Пусть данная граница проходит непосредственно перед комбинацией 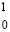 между многоточиями:
между многоточиями:
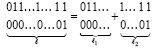 ,
,
где 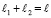 . Тогда преобразование в правой от границы части цепочки автоматически приведет к результату
. Тогда преобразование в правой от границы части цепочки автоматически приведет к результату
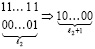 .
.
В то же время в левой от границы части цепочки ничего не изменится вследствие отсутствия преобразования (в левой части цепочки не было вертикально сдвоенной единицы переноса  ). В рассматриваемом случае единица переноса из правой части цепочки передается в младший разряд нижнего промежуточного ряда левой части, где образовавшаяся пара
). В рассматриваемом случае единица переноса из правой части цепочки передается в младший разряд нижнего промежуточного ряда левой части, где образовавшаяся пара  дает новую двухрядную цепочку переноса, а в правой части останется однорядная комбинация нулей:
дает новую двухрядную цепочку переноса, а в правой части останется однорядная комбинация нулей:
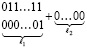 .
.
Чтобы иметь возможность продолжить процесс переноса, непосредственно слева от границы между соседними группами должна располагаться разрешающая параллельная схема элементов &. Следующим шагом для реализации переноса будет инициация этой схемы вертикальной парой  . Предлагается схему преобразования цепочки переноса, описанную до теоремы 2 (и в самой этой теореме), распространить сразу на две соседние группы. Когда цепочка переноса транзитно распространяется на две соседние группы, то помимо переноса из младшего разряда правой группы аналогичный перенос априори мог сформироваться в младшем разряде левой группы. Здесь по-прежнему необходимо учитывать, что после шага 1 все переносы, независимо от принадлежности к разным группам и расположениям возле границ групп, взаимно отделены вертикальными парами
. Предлагается схему преобразования цепочки переноса, описанную до теоремы 2 (и в самой этой теореме), распространить сразу на две соседние группы. Когда цепочка переноса транзитно распространяется на две соседние группы, то помимо переноса из младшего разряда правой группы аналогичный перенос априори мог сформироваться в младшем разряде левой группы. Здесь по-прежнему необходимо учитывать, что после шага 1 все переносы, независимо от принадлежности к разным группам и расположениям возле границ групп, взаимно отделены вертикальными парами  . В любом случае оба переноса взаимно отделены парами
. В любом случае оба переноса взаимно отделены парами  , и при распространении преобразования на две группы эти переносы не накладываются друг на друга. Оба таких переноса могут быть взаимно независимо и параллельно реализованы с помощью двух схем, каждая из которых аналогична схеме на рис. 2, при этом разрешающие параллельные схемы элементов & каждой из них располагаются слева от границы (в младшем разряде) своей группы. Схема в правой группе рассчитана на суммарное количество разрядов обеих групп 2(n + 1) / q, схема в левой группе – на количество разрядов своей группы (n + 1) / q. Две особенности схем для двух соседних групп в каждой рассматриваемой паре состоят в следующем. Обе разрешающие параллельные схемы элементов & инициируются вертикальными парами
, и при распространении преобразования на две группы эти переносы не накладываются друг на друга. Оба таких переноса могут быть взаимно независимо и параллельно реализованы с помощью двух схем, каждая из которых аналогична схеме на рис. 2, при этом разрешающие параллельные схемы элементов & каждой из них располагаются слева от границы (в младшем разряде) своей группы. Схема в правой группе рассчитана на суммарное количество разрядов обеих групп 2(n + 1) / q, схема в левой группе – на количество разрядов своей группы (n + 1) / q. Две особенности схем для двух соседних групп в каждой рассматриваемой паре состоят в следующем. Обе разрешающие параллельные схемы элементов & инициируются вертикальными парами  только в младших разрядах своих групп. В отличие от схемы на рис. 2 каждая инициированная схема не требует и не содержит разрешающих параллельных схем элементов &, сопоставленных всем разрядам внутри группы или двух групп, на которые она распространяется. Таким образом, сложность обеих схем измеряется только количеством разрядных элементов старших разрядов, на которые они распространяются, сложенным с количеством элементов разрешающих параллельных схем. Для двух смежных групп это составит
только в младших разрядах своих групп. В отличие от схемы на рис. 2 каждая инициированная схема не требует и не содержит разрешающих параллельных схем элементов &, сопоставленных всем разрядам внутри группы или двух групп, на которые она распространяется. Таким образом, сложность обеих схем измеряется только количеством разрядных элементов старших разрядов, на которые они распространяются, сложенным с количеством элементов разрешающих параллельных схем. Для двух смежных групп это составит 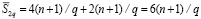 . В сумме по всем q/2 парам групп получится
. В сумме по всем q/2 парам групп получится 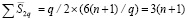 . На следующем шаге для продолжения переноса аналогично объединяются 4 группы. Соответственно число элементов схемы в объединенной четверке групп составит
. На следующем шаге для продолжения переноса аналогично объединяются 4 группы. Соответственно число элементов схемы в объединенной четверке групп составит 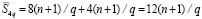 . В сумме по всем четверкам –
. В сумме по всем четверкам – 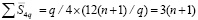 . В продолжение процесса попарного объединения смежных групп на шаге с номером k получится
. В продолжение процесса попарного объединения смежных групп на шаге с номером k получится
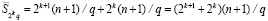 , и
, и
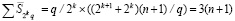 . (36)
. (36)
Процесс переноса завершится на шаге k, при котором q/2k = 1, или, 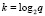 . Объединение оценок (35) и (36) дает полную сложность всего предложенного сумматора:
. Объединение оценок (35) и (36) дает полную сложность всего предложенного сумматора:
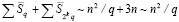 . (37)
. (37)
С учетом (34) время работы сумматора составит
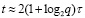 . (38)
. (38)
Если выбранное число групп q постоянно, то
t = O(1). (39)
Теорема 3. Пусть n + 1 является целой степенью по основанию 2, и пусть выбрано число q, также равное целой степени по основанию 2, причем q < n + 1, q – постоянное. Пусть все разряды слагаемых в порядке расположения разделены на q групп по n / q разрядов. Тогда рассматриваемое поразрядно-параллельное сложение двух (n + 1)-разрядных двоичных чисел вида (2), (3) с использованием разделения разрядов по группам выполняется за время, оцениваемое из (38), (39) независимо от числа разрядов. При этом количество элементов сумматора оценивается из (37), что в q раз меньше исходного количества (33).
Следствие 3. Если в условиях теоремы 3 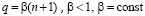 , то q – переменная,
, то q – переменная,
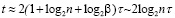 , (40)
, (40)
оценка (37) перейдет в оценку
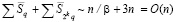 . (41)
. (41)
В условиях следствия 3 сумматор имеет сложность пропорциональную числу разрядов слагаемых и выполняет сложение за время O(log2n) инвариантно относительно n.
О производительности поразрядно-параллельной обработки в системе с параллельно-конвейерной архитектурой. Умножение можно выполнять посредством поразрядно-параллельного суммирования столбцов школьной схемы с диагональной записью результатов, образующих промежуточные ряды. Промежуточные ряды сжимаются в два ряда, затем их сумма определяется поразрядно-параллельно без вычисления переноса. Например,
В последней сверху вниз строке фигурной скобкой с равенством означен результат умножения, в двух непосредственно предшествующих ей фигурных скобках – два дополнительных шага поразрядно-параллельного сложения пары слагаемых. Первой сверху вниз фигурной скобкой отмечены слагаемые школьной схемы умножения, второй фигурной скобкой – результат их сжатия в три промежуточных ряда, третьей – результат сжатия в два промежуточных ряда, и ниже размечено поразрядно-параллельное суммирование двух таких слагаемых. В общем случае инвариантно относительно количества разрядов сомножителей получается логарифмическое от этого количества число шагов сжатия слагаемых школьной схемы до двухрядного кода и два дополнительных шага их перевода в однорядный двоичный код суммы. Умножение по такой схеме имеет логарифмическую оценку временной сложности: t = O(log2n).
В [1, 4] даны различные варианты схем умножения, некоторые с формально более высоким быстродействием (в рамках обсуждаемой темы ниже они не рассматриваются).
L = 8
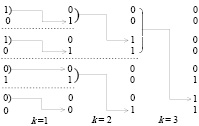
Рис. 3. Сложение L бит в унитарном коде
Метод в целом сводит потоковое сложение и потоковое умножение двоичных чисел исключительно к операциям вертикального сложения двоичных коэффициентов равного веса (к сложению бит). Сложение N бит без вычисления переноса реализуется за время O(log2n), один из вариантов схемы иллюстрирует рис. 3 (N = L = 8). В общем случае N бит располагаются по вертикали и разбиваются на пары. Верхний элемент пары сдвигается на позицию нижнего элемента, если нижний элемент равен 0, иначе смещение не выполняется (шаг k = 1). Полученный набор преобразованных пар в порядке расположения снова разбивается на пары (два упорядоченных бита в паре). В каждой паре два верхних бита сдвигаются вниз на количество позиций равное числу нулей сверху в нижней паре. Если в нижней паре сверху единица, сдвиг не выполняется (шаг k = 2). Аналогичное преобразование и смещение по вертикали сверху вниз выполняется на последующих шагах. За log2N шагов все входные единицы окажутся на выходе схемы упорядоченными без пропуска снизу вверх. Каждая единица на выходе схемы должна запирать выходной сигнал нижестоящей единицы. Тогда незапертой окажется только верхняя из единиц. Остается сопоставить каждой позиции единственной выходной единицы постоянные линии связи, соединение с которыми находится в соответствии единичным коэффициентам двоичного номера позиции при отсчете снизу вверх (шифратор). На выходе шифратора образуется двоичный код суммы N входных бит. Полностью логическая схема устройства представлена в [2]. По этой схеме (или с помощью известных аналогов) сумма N бит находится с временной сложностью
t = O(log2N), (42)
где оценка (42) может интерпретироваться как логарифмическая задержка логической схемы.
Пусть на время выполнения оценки рассматривается абстрактная вычислительная система, реализующая изложенный метод. Потенциал ее производительности можно оценить на примере суммирования потока слагаемых (1), где слагаемые разбиты на группы по N, и сложение в каждой группе доводится до однорядного прямого кода суммы. В этом случае суммирование в группе состоит из поразрядно-параллельного сложения N бит за время (42), затем из поразрядно-параллельного сжатия 1 + [log2N] промежуточных рядов, где число шагов m-кратного сжатия (до получения двухрядного кода промежуточных слагаемых) зависит только от априори фиксированного N и является постоянным. Число m рассчитывается элементарно: в соотношении сжатия до двух промежуточных рядов,
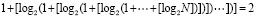 ,
,
выражение 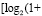 повторяется столько раз, сколько шагов нужно выполнить, чтобы это равенство стало верным. Если, например, N = 10240, то после первичной обработки входного набора число промежуточных рядов станет равным 1 + [log210240] = 14.
повторяется столько раз, сколько шагов нужно выполнить, чтобы это равенство стало верным. Если, например, N = 10240, то после первичной обработки входного набора число промежуточных рядов станет равным 1 + [log210240] = 14.
При первом сжатии их число сократится до 1 + [log214] = 4. Второе сжатие влечет 1 + [log24] = 3. Третье сжатие приводит к двум промежуточным рядам: 1 + [log23] = 2. В данном случае m = 3. В общем случае время выполнения m-кратного сжатия составит 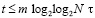 , при этом
, при этом 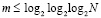 в случае N ≤ 10240. Далее, два промежуточных слагаемых поразрядно-параллельно преобразуются за два шага в прямой однорядный двоичный код суммы за время t = O(1). Объединение всех составляющих шагов влечет оценку временной сложности для текущей группы T = O(log2N). Подсоединение однорядного двоичного слагаемого к каждой новой группе входных слагаемых не изменит вид этой оценки (N заменяется на N + 1) . В результате весь поток (1) будет обработан с временной сложностью
в случае N ≤ 10240. Далее, два промежуточных слагаемых поразрядно-параллельно преобразуются за два шага в прямой однорядный двоичный код суммы за время t = O(1). Объединение всех составляющих шагов влечет оценку временной сложности для текущей группы T = O(log2N). Подсоединение однорядного двоичного слагаемого к каждой новой группе входных слагаемых не изменит вид этой оценки (N заменяется на N + 1) . В результате весь поток (1) будет обработан с временной сложностью
T = O(log2N) × P / N. (43)
Оценка (43) формально не зависит от числа разрядов слагаемых. Вместе с тем она может быть улучшена в условиях специальной архитектуры вычислительной системы. Поскольку при каждом суммировании группы слагаемых все шаги обработки состоят из чередующихся однотипных операций, то процесс суммирования потока можно разложить на сегменты конвейера, соответственные каждому шагу (каждой операции). Такой конвейер имеет логарифмическую глубину загрузки O(log2N), такт конвейера имеет длительность O(1), соизмеримую со временем переключения элемента. После загрузки в каждом такте конвейер принимает новый набор из N двоичных слагаемых потока (1). Временная сложность конвейера улучшает оценку (43) за счет сокращения длительности обработки текущей группы N двоичных слагаемых до одного такта. В результате
T = O(P / N). (44)
Для арифметики с вычислением переноса глубина загрузки конвейера на практике тактируется более длительно, время его работы зависит от числа разрядов слагаемых.
Потенциал роста производительности не исчерпывается организацией предложенного конвейера. Без изменения математической основы рассматриваемый конвейер увеличит производительность в два раза за счет использования параллельной работы двух таких конвейеров, при условии, что выход второго подключен к входу первого. При этом выходная сумма второго подсоединяется в качестве дополнительного слагаемого к входному набору слагаемых первого, а оба конвейера независимо друг от друга в каждом такте принимают на вход по одному новому набору из N слагаемых потока (1). В сумме это влечет 2N слагаемых в каждом такте. Если аналогично объединяются три конвейера, то производительность обработки потока вырастет в три раза (3N слагаемых в такте) и т.д. Количество объединяемых параллельно работающих конвейеров формально не ограничено. Ниже показано расположение данных при объединении в одну параллельно-конвейерную вычислительную систему p исходно описанных конвейеров при обработке потока (1). Все p конвейеров работают параллельно, в каждом такте каждый из них принимает на вход новый набор N слагаемых, что в (45) отмечено угловыми стрелками. Выход i+1-го конвейера подключен ко входу i-го
 (45)
(45)
при каждом  , с тем чтобы (i+1)-й передавал вычисленную им сумму
, с тем чтобы (i+1)-й передавал вычисленную им сумму 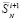 на вход i-го, где i-й конвейер подсоединяет
на вход i-го, где i-й конвейер подсоединяет 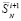 к своему новому входному набору. Как вариант организации вычислений, сумма
к своему новому входному набору. Как вариант организации вычислений, сумма 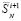 может представляться в двухрядном коде. Производительность такой параллельно-конвейерной системы в p раз выше производительности одного отдельно взятого конвейера (pN слагаемых в каждом такте), оценка (44) перейдет в соответственную оценку временной сложности рассматриваемой системы
может представляться в двухрядном коде. Производительность такой параллельно-конвейерной системы в p раз выше производительности одного отдельно взятого конвейера (pN слагаемых в каждом такте), оценка (44) перейдет в соответственную оценку временной сложности рассматриваемой системы
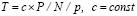 . (46)
. (46)
В частности, при p = N (46) примет вид
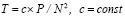 . (47)
. (47)
Оценки (46), (47) непосредственно не выражают значение τ. При достаточно большом числе слагаемых потока (1), 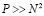 , в каждом такте длительности τ параллельно-конвейерной системы вычисляется новая сумма pN и соответственно N2 чисел вида (2). Если, например, N = 103, то N2 = 106, и система за такт единичной длительности вычисляет сумму 106 слагаемых. Оценка корректируется в зависимости от длительности τ. Если τ = 10–3 сек, то суммируется 109 слагаемых в секунду. Если τ = 10–6 сек, то суммируется 1012 слагаемых в секунду и т.д. Если же при N = 103 по схеме (45) объединяются p = N2 конвейеров, то за такт единичной длительности суммируется 109 слагаемых, если в этом случае τ = 10–3 сек, то в секунду суммируется 1012 слагаемых, при τ = 10–6 сек в секунду суммируется 1015 двоичных слагаемых и т.д.
, в каждом такте длительности τ параллельно-конвейерной системы вычисляется новая сумма pN и соответственно N2 чисел вида (2). Если, например, N = 103, то N2 = 106, и система за такт единичной длительности вычисляет сумму 106 слагаемых. Оценка корректируется в зависимости от длительности τ. Если τ = 10–3 сек, то суммируется 109 слагаемых в секунду. Если τ = 10–6 сек, то суммируется 1012 слагаемых в секунду и т.д. Если же при N = 103 по схеме (45) объединяются p = N2 конвейеров, то за такт единичной длительности суммируется 109 слагаемых, если в этом случае τ = 10–3 сек, то в секунду суммируется 1012 слагаемых, при τ = 10–6 сек в секунду суммируется 1015 двоичных слагаемых и т.д.
Замечание 5. Абстрактно можно рассматривать группы разбиения потока (1) не по N, а по N2 слагаемых, которые в таком виде поступают на вход каждого конвейера. Нужно иметь в виду, что такие наборы слагаемых для вертикального сложения бит в каждом разряде допускают естественное распараллеливание по группам бит с несложным объединением сумм в группах в единую вертикальную сумму бит данного веса разряда. В этом случае в зависимости от конкретной длительности такта τ оценки производительности возрастут до более высоких значений. За такт единичной длительности будет суммироваться 1012 слагаемых. Если τ = 10–3 сек, то в секунду будет суммироваться 1015 слагаемых, при τ = 10–6 сек в секунду будет вычисляться сумма 1018 двоичных слагаемых и т.д.
Формально эти оценки, как и (43), (46), (47), не зависят от числа разрядов слагаемых. Насколько корректна такая абстракция, можно сопоставить приведенные оценки с оценками производительности действующих суперкомпьютеров. Так, самый мощный суперкомпьютер в мире на 2021 г. Fugaku [9] имеет архитектуру с 7 миллионами 630 тысячами 848 ядрами, по результатам тестирования High Performance Linpack получен результат в 442 петафлопса (442 квадриллиона, или 442 × 1015, операций с плавающей точкой за секунду). Суперкомпьютер размещается в 432 стойках. Тестирование проводилось не на операциях сложения двоичных полиномов, а на специальных задачах с разнообразием арифметических операций с плавающей точкой. Это, однако, заведомо исключает независимость оценок производительности от числа разрядов данных, кроме того при обработке потока (1) оценки не сохранятся.
Замечание 6. Предложенный метод, будучи поразрядно-параллельным, в исходном варианте остается последовательным по шагам алгоритма выполнения арифметических операций. Реализация исходного метода предполагает последовательное программное управление, что не повлечет необходимость сотен стоек для размещения вычислительной системы.
Параллельно-конвейерная вычислительная система допускает адаптацию к потоку сомножителей, а также к потоку любых однотипных арифметических операций, являющихся композицией сложений и умножений, например к операциям суммы парных произведений (скалярное произведение векторов), умножения матрицы на столбец, на матрицу, умножения матрицы на вектор и сложение с вектором и другие.
О границах числа разрядов данных при поразрядно-параллельной обработке без вычисления переноса. Обработка без ограничения числа разрядов выше рассматривалась абстрактно, желательно оценить длину разрядной сетки в аспекте потенциальной реализации предложенного метода. Как правило, в компьютерах с 64-битной разрядной сеткой мантиссы (вычисления с плавающей точкой с двойной точностью) диапазон представления чисел определяется неравенствами α × 2–52 × 2–1022 < a < β × 21024, где α, β – постоянные коэффициенты (в специализированных архитектурах возможны другие данные [10], ниже они не рассматриваются). Это означает, что число a для своего представления в позиционной двоичной системе требует не более 1074 разрядов, заведомо достаточно 2048 разрядов. Если вести арифметическую обработку с фиксированной точкой в диапазоне 2048 разрядов при ограничении, что число разрядов входных данных составляет не более n + 1 = 64, то для реализации рассматриваемого метода потребовалось бы 211 параллельно работающих разрядных элементов. Современные сверхбольшие интегральные схемы (СБИС) насчитывают 106 > 29 и более элементов. Объединение 4 таких СБИС в одной вычислительной системе формально решало бы проблему (в процессорах производства TSMC (AMD) по 7-нм техпроцессу 113,9 млн транзисторов на мм² [11]). В аспекте погрешности целесообразно принять во внимание, что вычисления с фиксированной точкой выполняются без операции «механического» сдвига при выравнивании порядков, поэтому при их выполнении не теряются значащие цифры операндов и результатов обработки. В то же время в процессе сложения с плавающей точкой потеря значащих цифр мантиссы происходит в результате физического сдвига мантиссы: младшие разряды выходят за пределы фиксированной разрядной сетки и теряются, при округлении результатов умножения для сохранения длины разрядной сетки отбрасывается половина младших разрядов мантиссы произведения. В операциях с плавающей точкой потери значащих цифр мантиссы представляют собой практически неконтролируемый процесс. Как альтернативу, для реализации предложенного метода можно рассматривать длину разрядной сетки входных и текущих данных до n + 1 = 211 и более. При поразрядно-параллельной арифметической обработке без вычисления переноса естественный параллелизм разрядных операций позволяет разделять обработку разрядов данных на взаимно независимые части, аналогично тому, как это рассматривалось в случае сложения чисел с формально не ограниченным числом разрядов. Разделенные части допускают параллельную синхронную обработку с простым обменом по фиксированным линиям связи. Приемлемый диапазон данных для обработки с фиксированной точкой можно выбрать с учетом оценок (38), (39) и (40), (41).
Вместе с тем для реализации обработки с фиксированной точкой возникают математические, схемные и технологические трудности. Первая из них – рост числа разрядов данных по ходу вычислений. Например, с каждым последовательным умножением длина разрядной сетки будет возрастать на n, при каждом умножении числа на себя она будет удваиваться. Миллиарды операций в секунду будут приводить к миллиардным значениям числа разрядов данных. Абстрактно можно рассматривать запись промежуточных данных в память по принципу счетчика, обсуждавшуюся вначале (рис. 1). Более реалистично при каждом достижении априори заданной (по возможности высокой) границы числа разрядов округлять дробную часть числа до фиксированного количества разрядов. Можно допускать смешанный вариант обработки: до априори заданной границы числа разрядов вычисления выполняются с фиксированной точкой, при достижении границы выполняется округление дробной части. Если в ходе операций с округленным числом разрядов длина разрядной сетки превзойдет априори заданное значение, можно рассматривать переход на операции с плавающей точкой.
Вторая трудность поразрядно-параллельной обработки с длинной разрядной сеткой заключается в том, что существующие микросхемы требуют минимального числа внешних контактных соединений. Если в таких ограничениях ввод-вывод данных будет выполняться последовательно по разрядам, эффективность параллельной обработки разрядов будет падать с ростом числа разрядов. Если же ввод-вывод данных будет выполняться параллельно по разрядам, потребуется число внешних контактов, превосходящее допустимые технологические ограничения. Основой решения проблемы может служить естественный параллелизм обработки одновременно всех разрядов данных. Множество разрядов каждого из двух операндов с длинной разрядной сеткой можно разделять на равные части так, что в каждой части оказывается количество разрядов n0, где n0 не превосходит требуемого ограничения, например, n0 ≤ 32. Каждая часть из n0 разрядов может записываться в сопоставленный модуль запоминающего устройства, а также считываться из него согласно известному способу организации памяти. Составные части операндов при этом обрабатываются взаимно независимо, параллельно и синхронно на сопоставленных разрядных элементах. Результаты частичной обработки затем объединяются в окончательное значение всех разрядов каждого выходного данного на основе обмена по фиксированным линиям связи между разрядными элементами, при этом учитываются схемные решения, описанные выше для сложения чисел с произвольным числом разрядов: n0 = (n + 1) / q, – теорема 3, следствие 3, оценки (37)–(41).
Отдельную трудность определяет существующая структура памяти, где адресация к ячейкам также имеет ограничение на число входов. Основой для решения может служить разделение разрядов данного на части по n0 разрядов. Если каждой такой части взаимно однозначно сопоставить отдельный модуль памяти, рассчитанный на n0 бит, то между всеми частями разрядов операнда и множеством сопоставленных модулей памяти устанавливается взаимно однозначное соответствие. В этом случае каждая часть из n0 разрядов и каждый модуль памяти из n0 бит могут взаимодействовать, как в последовательных устройствах, – с отдельным устройством адресации и считывания по фиксированным линиям связи. При этом запись и считывание могут выполняться параллельно и синхронно по всем частям разрядов и по всем соответственным модулям памяти. Обращение к памяти можно организовать взаимно независимо по всем параллельно работающим устройствам. Возможна единая адресация для всего операнда, где адрес его записи или считывания дублируется на каждый модуль. При этом модуль памяти к единому адресу добавляет свой фиксированный номер, а последующий процесс записи и считывания автоматически учитывает суммарный адрес. Адресованные данные по фиксированным линиям связи поступают в разрядные элементы, соответственные считанной группе разрядов, и обратно. На этой основе можно рассматривать совмещение метода с существующей элементной базой.
Если метод в целом не ориентировать на создание специальной элементной базы и архитектуры вычислительной системы, то по своей конструкции он может использоваться для увеличения производительности и снижения погрешности вычислительной обработки путем ускорения операций (за счет отсутствия вычисления переноса) и непосредственного удлинения разрядной сетки.
Некоторые сравнительные оценки. В заключение можно отметить, что распространение метода на точный поиск сверхдлинных слов обсуждается в [6], на быстрое преобразование структур данных – в [7]. Изложенные результаты сравнимы с известными, в частности, в следующих аспектах. Тематика работы сохраняет актуальность от начала создания вычислительных систем [12–14]. В исходном варианте предложенный метод позволяет сохранить последовательное программное управление, тогда как параллельное программное управление критически сложно в отношении эффективности использования многопроцессорных вычислительных систем [15]. Существующие методы синтеза параллельных сумматоров основаны на преобразованиях булевых формул и функций [14]. Известные оценки временной сложности параллельных сумматоров имеют вид 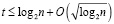 [14, 16] и
[14, 16] и 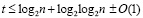 [17], в [14, 18] приводится оценка
[17], в [14, 18] приводится оценка 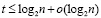 , сумматоры имеют линейную сложность, порядок временной сложности не улучшается вследствие логарифмической нижней оценки глубины схемы [14, 18]. В излагаемой работе сумматор построен без преобразований булевых формул и функций, имеет временную сложность t = O(1) независимо от числа разрядов (теоремы 2, 3), но число его элементов (в начальной версии) является квадратичным. С другой стороны, функциональные возможности метода, лежащего в основе построения сумматора, позволяют адаптировать его к сверхдлинной разрядной сетке, распространяются на групповую обработку числовых данных, расширяются до уровня организации параллельно-конвейерной системы без вычисления переноса.
, сумматоры имеют линейную сложность, порядок временной сложности не улучшается вследствие логарифмической нижней оценки глубины схемы [14, 18]. В излагаемой работе сумматор построен без преобразований булевых формул и функций, имеет временную сложность t = O(1) независимо от числа разрядов (теоремы 2, 3), но число его элементов (в начальной версии) является квадратичным. С другой стороны, функциональные возможности метода, лежащего в основе построения сумматора, позволяют адаптировать его к сверхдлинной разрядной сетке, распространяются на групповую обработку числовых данных, расширяются до уровня организации параллельно-конвейерной системы без вычисления переноса.
Заключение
В работе показана возможность выполнения групповых и бинарных арифметических операций без вычисления переноса, что позволяет вести обработку параллельно по всем разрядам операндов с удлиненной разрядной сеткой. Используемая арифметика эквивалентна обычной арифметике, обладает потенциалом увеличения производительности и снижения погрешности вычислительной обработки в компьютере с архитектурой, проектируемой на ее основе, в начальной версии архитектуры сохраняется последовательное программное управление.



