Сглаживающие кубические сплайны (СКС) находят широкое применение для фильтрации шумов измерений экспериментальных данных или, другими словами, для сглаживания зашумленных данных [1, 2]. К основному преимуществу СКС по сравнению с другими алгоритмами фильтрации можно отнести тот факт, что сглаживающий сплайн и его первые две производные являются непрерывными функциями на всем интервале построения сплайна. Это позволяет использовать СКС для устойчивого вычисления производных по зашумленным измерениям обрабатываемой функции, в частности в задачах непараметрической идентификации как линейных [3–5], так и нелинейных [6, 7] динамических систем. Для последнего класса систем СКС используется для вычисления смешанных производных [8]. СКС имеет некоторый управляющий параметр – параметр сглаживания, от величины которого существенно зависит ошибка сглаживания зашумленных данных [2, 9]. Выбор этого параметра является основной проблемой при использовании сглаживающих сплайнов на практике. Предложены несколько алгоритмов выбора, позволяющие с приемлемой для практики точностью оценить оптимальное значение параметра сглаживания (ошибка сглаживания минимальна) при различной априорной информации о дисперсии шума измерений [2, 8]. Хотя СКС по принципу своей работы является низкочастотным фильтром (удаляющим высокочастотные – шумовые составляющие обрабатываемого сигнала) традиционный подход к построению СКС не позволяет интерпретировать СКС как такой фильтр и, как следствие, решать задачи анализа и синтеза СКС в терминах низкочастотного фильтра и его характеристик, которые естественны и понятны экспериментатору.
Поэтому в данной работе предлагается частотная модель СКС и вводятся динамические характеристики СКС, позволяющие решать задачи анализа и синтеза СКС как низкочастотного фильтра, а именно:
− строится амплитудно-частотная характеристика СКС, включающая все основные параметры СКС;
− вводятся понятия аппаратной функции сплайна и эквивалентной ширины аппаратной функции сплайна;
− предлагается процедура синтеза СКС (выбор параметра сглаживания) по заданной величине эквивалентной ширины аппаратной функции.
Материалы и методы исследования
В начале приведём некоторые определения, нужные для построения частотной модели СКС [1, 9]. Предположим, что на интервале [T1,T2] заданы n узлов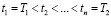 
и в этих узлах измерены значения функции:
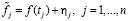, (1)
где ηi – случайный шум (погрешность) измерений с нулевым средним и дисперсией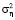 
(равноточные измерения). Функция Sn,α(t) называется сглаживающим кубическим сплайном дефекта единица, если: а) на каждом отрезке 
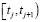функция Sn,α(t) является кубическим многочленом вида
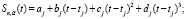(2)
б) функция Sn,α(t) дважды непрерывно дифференцируема на всём интервале [T1,T2].
Сглаживающий кубический сплайн Sn,α(t) в общем случае не проходит через точки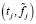 
, а проходит в некоторой окрестности (ее размеры определяются величиной параметра сглаживания) от этих точек, обеспечивая тем самым сглаживание (фильтрацию) шума измерений. Для однозначного определения коэффициентов СКС (2) в узлах t1, tn задаются краевые условия сплайна, из которых наиболее часто используют:
− условия на значения первой производной вида
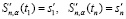; (3)
− условия на нулевые значения второй производной
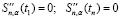; (4)
− или сочетание условий (3), (4) (например, в узле t1 задается (3), а в tn – условие (4)).
Доказано, что СКС, построенный при краевых условиях (3) или (4), доставляет минимум функционалу [1]:
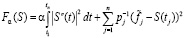, (5)
где pj – весовые множители, отражающие точность j-го измерения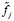 
(в случае равноточных измерений задаются одинаковыми, например 
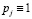), α – параметр сглаживания.
Перейдем к построению частотной модели СКС. Для этого представим СКС в виде «черного» ящика, на вход которого поступает последовательность измеренных значений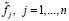 
, а выходом является функция Sn,α(t) с непрерывными производными до второй включительно и определенная на интервале [T1,T2]. При этом будем полагать, что шаг сетки равный и равен Δt и весовые множители pj одинаковы и равны p.
Первоначально установим связь между значениями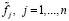 
, и вторыми производными Mj сплайна Sn,α(t) в узлах tj. За исключением двух первых и двух последних узлов эта связь выражается следующим разностным уравнением [1, 2]:
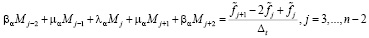. (6)
В формуле (6)
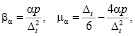
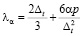. (7)
Уравнение (6) отражает структуру дискретного фильтра, преобразующего входную последовательность {f̃j} в последовательность {Mj}. Для построения частотной характеристики такого фильтра обратимся к так называемому D-преобразованию бесконечной последовательности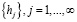 
, определяемому соотношением
.
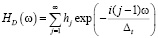где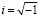 
. Заметим, что HD(ω) является периодической функцией с периодом 2π / Δt. Обозначим через 
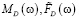– D-преобразования дискретных последовательностей {Mj}, {f̃j}. Тогда частотная характеристика рассматриваемого дискретного фильтра определяется как отношение 
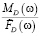. С учетом свойств D-преобразова-ния для сдвинутых последовательностей 
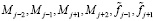[ ], получаем частотную характеристику дискретного преобразования {f̃j} ⇒ {Mj}:
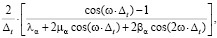
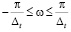(8)
Далее рассмотрим преобразование дискретных значений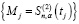 
второй производной в непрерывную вторую производную сплайна:
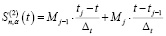, (9)
что соответствует линейной интерполяции с частотной характеристикой:
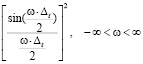. (10)
Для нахождения Sn,α(t) по второй производной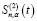 
выполним двойное интегрирование, что соответствует преобразованию с частотной характеристикой:
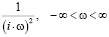. (11)
Очевидно, что частотная характеристика СКС равна произведению частотных характеристик (8), (10), (11) и определяется выражением
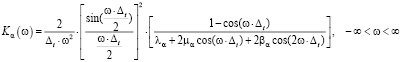. (12)
Характеристика (12), по сути, является амплитудо-частотной характеристикой динамического звена {f̃j} ⇒ {Mj}. Введем понятие аппаратной функции СКС kα(t) как обратное преобразование Фурье от частотной характеристики (12):
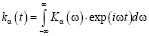. (13)
Возникает вопрос: как использовать понятия частотной характеристики и аппаратной функции СКС для его анализа и синтеза? Предположим, что функция f(t) имеет Фурье-образ, равный ФF(ω). Тогда Фурье-образ ФSα(ω) сплайна Sn,α(t), построенного по точным значениям {fj = f(tj)}, будет определяться выражением
ФSα(ω) = Kα(ω)ФF(ω), – ∞< ω < ∞. (14)
В соответствии с теоремой о свертке [10, с. 527–529], сплайн Sn,α(t) можно представить как результат интегрирования:
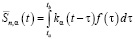(15)
и его можно интерпретировать как «усреднение» функции f(t) аппаратной функцией сплайна. Очевидно, что чем меньше «ширина» аппаратной функции, тем меньше Sn,α(t) отличается от f(t) и тем меньше систематическая ошибка сглаживания. Для количественной оценки ширины аппаратной функции введем характеристику, которую назовем эквивалентной шириной аппаратной функции (ЭШАФ) W(α):
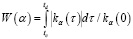. (16)
Величина W(α) уже позволяет говорить о разрешающей способности СКС, а именно: если функция имеет две δ-образных структуры, то они проявятся в СКС (возможно, в сглаженном виде), если «расстояние» (по шкале аргумента t) между ними будет не меньше W(α) (см. результаты вычислительного эксперимента).
Замечание. В силу конечной длительности функций f(t), k(τ) пределы интегрирования ta, tb, tc, td в (15), (16) имеют конечные значения, что позволяет вычислить (15), (16), применяя подходящие квадратурные формулы.
Таким образом, введение характеристики W(α) позволяет говорить об анализе разрешающей способности СКС – когда по заданному параметру сглаживания вычисляется значение W(α) и о задаче синтеза СКС – когда по заданному максимальному значению W(α) вычисляется величина параметра сглаживания. Так как сглаживающая способность сплайна увеличивается по мере возрастания параметра сглаживания и W(α) при этом также увеличивается, то, решая задачу синтеза сплайна по заданной максимальной величине W(α), можно говорить о построении сплайна с наименьшим уровнем случайной ошибки среди всех сплайнов с ЭШАФ не более W(α).
Результаты исследования и их обсуждение
Первоначально рассмотрим результаты вычисления частотной характеристики (12) и аппаратной функции (13) сплайна с параметрами Δt = 0.05, p = 1. На рис. 1 изображены графики частотной характеристики Kα(ω) при разных параметрах сглаживания: сплошная кривая – α = 0; штриховая кривая – α = 0.0001. точечная кривая – α = 0.1. На рис. 2 показаны графики аппаратных функций сплайна при тех же параметрах сглаживания (соответствие типов кривых те же, что и на рис. 1). Хорошо видно, что при увеличении параметра сглаживания уменьшается ширина полосы пропускания СКС (как низкочастотного фильтра), а следовательно, увеличивается подавление шума измерений, но при этом увеличивается ширина аппаратной функции, что вызывает ухудшение разрешающей способности сплайна – известное противоречие между систематической и случайной составляющей ошибки фильтрации любого линейного алгоритма фильтрации.
Перейдем к рассмотрению эквивалентной ширины аппаратной функции СКС, определяемой соотношением (16). На рис. 3 представлен график характеристики W(α) от параметра сглаживания. Используя этот график, попробуем определить параметр сглаживания по заданной величине W(α) = WS = 0.2. Для этого по оси ординат (рис. 3) откладываем величину 0.2 и проводим штриховую прямую до пересечения с графиком W(α) (точка пересечения обозначена буквой А), а затем из этой точки опускаем перпендикуляр на ось абсцисс – и точку пересечения с этой осью обозначим как В. Значение α в точке В примерно равно α0.2 = 3 ∙ 10–4, и, по сути, это значение является «графическим» решением нелинейного уравнения W(α) = WS.
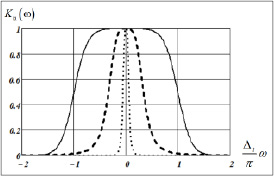
Рис. 1. https://s.top-technologies.ru/pic/2022/5-1ная характеристика СКС при различных значениях параметра α
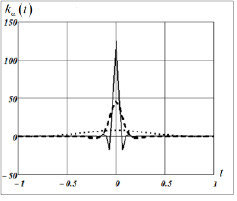
Рис. 2. Аппаратная функция СКС при различных значениях параметра α
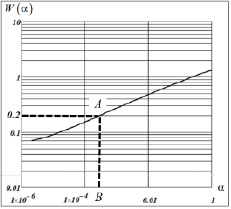
Рис. 3. Зависимость характеристики W(α) от параметра сглаживания α
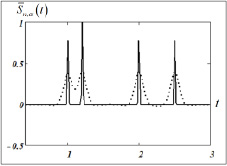
Рис. 4. СКС при заданной разрешающей способности
На рис. 4 показаны графики четырех δ-образных функций. Расстояние между левой парой кривых равно 0,2, т.е. равно заданной величине WS, а расстояние между правой парой равно 0.5. Точечной кривой на рис. 4 показаны значения сглаживающего сплайна, построенного при α0.2 = 3 ∙ 10–4.
Видно, что в сплайне четко «проявились» две левых δ-образных функций, расстояние между которыми равно заданной величине ЭШАФ построенного СКС. Следовательно, по величине ЭШАФ сплайна можно определить расстояние между «тонкими» деталями функции, сохраненные в построенном СКС, т.е. можно говорить о разрешающей способности СКС, которую можно характеризовать ЭШАФ. Так как расстояние между правыми δ-образных функций в 2,5 раза больше заданной ЭШАФ, то эти функции полностью сохранились в построенном СКС.
Заключение
Предложенная в работе частотная модель СКС позволяет интерпретировать сглаживающий сплайн как низкочастотный фильтр, полоса пропускания которого зависит от параметра сглаживания. Введенная аппаратная функция сплайна и ее эквивалентная ширина дает возможность определить разрешающую способность СКС, и это позволяет решать:
− задачу анализа СКС – когда по заданному параметру сглаживания определяют введенные частотные и временные характеристики сплайна;
− задачу синтеза СКС – когда по заданной ЭШАФ WS находят значение параметра сглаживания СКС путем решения нелинейного уравнения W(α) = WS численными методами.
Исследование выполнено при финансовой поддержке РНФ в рамках научного проекта № 22-21-00409.