Современные труды молодых ученых в области физической культуры и спорта разнообразны, но чаще всего посвящены проблемам совершенствования процесса формирования физических качеств у представителей различных возрастных групп или организации тренировочной деятельности на основе применения инновационных подходов. Эффективность разрабатываемых методических рекомендаций или построенных моделей может быть подтверждена посредством проверки статистических гипотез. Наиболее распространенным инструментом в этом случае является критерий Стьюдента, имеющий две модели:
− для сравнения данных в случае связанных выборок (например, сопоставление данных по одной и той же группе, зарегистрированных до и после экспериментального воздействия);
− для несвязанных выборок (в частности, выявление значимых различий в контрольной и экспериментальной группах).
Исследователи объясняют востребованность данного критерия его многофункциональностью: он позволяет оценить однородность выборок (доказать их принадлежность к одной генеральной совокупности), значимость различий между средними выборочными. Применение критерия позволяет построить интервальную оценку генеральной средней или средней дисперсии на основе взаимосвязи трех основных характеристик выборочной совокупности: «ширины доверительного интервала, соответствующей ему доверительной вероятности и объема выборки» [1, с. 43].
Перечисленные преимущества t-критерия Стьюдента в области физической культуры и спорта не имеют такой выраженности, так как его использование ограничено двумя требованиями:
− нормальное распределение сопоставляемых выборочных данных;
− равенство дисперсий.
В научно-методической литературе описываются трудности проверки нормальности распределения и равенства дисперсий, а также последствия нарушений хотя бы одного из этих условий. В частности, одним из условий корректности проверки является существенное увеличение объема выборок (до 2500), что невыполнимо для малых массивов данных. В этих условиях рекомендуется использование критерия Крамера – Уэлча, где «разность выборочных средних арифметических для двух выборок делится на естественную оценку среднего квадратического отклонения этой разности» [2, с. 12].
Если сопоставление производится для большего количества групп или объем выборок относительно мал, то решение данной задачи при помощи параметрических критериев в ряде случаев некорректно [3, с. 120].
Отбор непараметрических критериев для сопоставления результатов измерений осуществляется на основе учета следующих факторов: количество сопоставляемых выборок и объем каждой из сопоставляемых выборок. При этом необходимо также учитывать относительную мощность отбираемых критериев. Если сопоставляются две выборки с целью выявления различий между ними по уровню одного исследуемого признака, то чаще всего используются два непараметрических критерия. Молодые исследователи испытывают сложности при выборе между критерием Розенбаума и критерием Манна – Уитни.
С целью решения представленных выше проблем был произведен сравнительный анализ непараметрических критериев, используемых в современной практике статистического анализа данных малого объема.
Цель исследования – определить условия, при которых использование критерия Манна – Уитни будет целесообразным; описать приведенные в специальной литературе подходы к расчету значения критерия Манна – Уитни и выявить возможные несоответствия между результатами их применения.
Материалы и методы исследования
При проведении исследования осуществлен сравнительный анализ материалов, представленных в открытых информационных источниках. Описанные математические модели применены для обработки данных по оценке уровня физического развития подростков. Произведено сопоставление результатов в формальном и графическом представлении при помощи онлайн-калькуляторов.
Результаты исследования и их обсуждение
Проблема выбора критерия для сравнения данных выборок малого объема по уровню исследуемого признака широко рассматривается в современной специальной литературе. Для параметрических критериев необходима первоначальная проверка нормального распределения сопоставляемых данных [4, с. 56].
Данная процедура связана с использованием целого ряда критериев, имеющих собственную квалификацию и систему ограничений применимости [5, с. 83].
Указанные трудности игнорируются при проверке гипотезы о равенстве выборочных средних посредством использования непараметрических критериев.
Если сопоставляются данные для двух зависимых выборок малого объема, то чаще всего используется Q-критерий Розенбаума. Такой отбор определяется условием сопоставимости объема сравниваемых выборок (в частности, их равенства). Существенным недостатком Q-критерия является ограничение объема выборок (не более 10 наблюдений в каждом).
U-критерий Манна – Уитни является более мощным. Достаточно, чтобы объем каждой выборки превысил два наблюдения при верхней границе 60 наблюдений, определяемой таблицей критических значений. Возможно применение U-критерия даже при условии, когда объем одной выборки равен 2, а объем другой больше 4.
Позиционирование критерия Манна – Уитни в системе отбора непараметрических критериев представлено в научно-методической литературе (рис. 1).
Для использования критерия необходимо объединить выборочные данные и проранжировать их. Затем следует вновь разделить выборки. Критерий сводится к оценке зоны пересечения проранжированных данных. Чем эта зона меньше, тем существеннее различия.
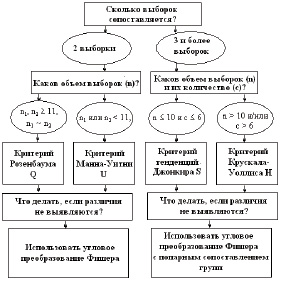
Рис. 1. Система отбора непараметрического критерия для определения различий в выборках по уровню исследуемого признака
Расчетное значение находится следующим образом:
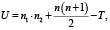
где n1 – объем первой выборки;
n2 – объем второй выборки;
n – объем выборки, имеющей большую ранговую сумму;
T – большая сумма рангов выборок [6, с. 52]
В открытых информационных источниках представлен еще один вариант определения расчетного значения U-критерия:
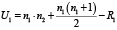 ,
,
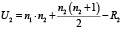 ,
,
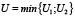 ,
,
где R1 – ранговая сумма первой выборки;
R2 – ранговая сумма второй выборки [7].
Вопрос идентичности результатов использования расчетных формул не рассмотрен подробно в современных научных трудах.
Приведем пример расчета U-критерия для выборочных данных, не имеющих нормального распределения. При исследовании реакции выбора у мальчиков-подростков был произведен подсчет количества ошибок, совершаемых в стандартных условиях. В первой группе количество тренировок превышало 13 ч в неделю, во второй объем тренировок был меньше 13 ч в неделю. Результаты расчетов представлены в таблице.
I способ расчета:
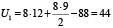 ,
,
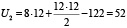 ,
,
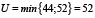 .
.
II способ расчета:
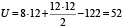 .
.
Наблюдаемые различия в результатах расчетов могут быть проигнорированы, так как в обоих случаях происходит отклонение нулевой гипотезы (критическое значение U-критерия равно 22, то есть существенно меньше расчетного). Однако отсутствие идентичности результатов является значительным недостатком критерия.

Рис. 2. Результаты расчета U-критерия при помощи программы medstatistic.ru/calculators
Современные сервисы обеспечивают возможность онлайн-расчета значения критерия, при этом отмечается, что результаты могут существенно отличаться в зависимости от того, учтена ли поправка на непрерывность. В случае аппроксимации генеральной совокупности и при рассмотрении выборки малого объема с дискретными значениями могут быть получены заключения о значимости и незначимости различий связанных рангов для одних и тех же массивов данных.
В рассмотренном случае очевидно, что различия несущественны, так как наблюдается тотальное пересечение рядов рангов. При этом результаты калькуляции, представленные бесплатными программами расчета, отличаются (рис. 2, 3).
Описанные выше несоответствия расчетных характеристик процедуры проверки статистической гипотезы об отсутствии значимых различий средних значений для независимых выборок на основе использования непараметрического критерия Манна – Уитни предполагают многоаспектный подход к анализу экспериментальных данных. В частности, необходима более глубокая детализация в случае использования электронных систем оценки. Для дискретных характеристик следует применять способ расчета U-критерия для каждой из ранговых сумм и минимизации полученных результатов.

Рис. 3. Результаты расчета U-критерия при помощи программы Mann – Whitney U Test Calculator
Заключение
«Ручной» способ ранжирования данных с количеством градаций, превышающем 20, и их дальнейшей обработки является трудоемким и нецелесообразным. Ранее в этом случае для сравнения выборочных средних применялось угловое преобразование Фишера. Современные сервисы предоставляют возможность расчета критерия Манна – Уитни для малых выборок, не имеющих нормального распределения с относительно большим количеством градаций. Данная процедура предполагает аппроксимацию данных к непрерывному распределению, что может дать некорректный или неоднозначный результат. Для исключения таких трудностей следует использовать сопоставление результатов использования двух схем расчета. Возможно представление ранжированных значений посредством применения возможностей графических редакторов. Визуальная оценка ширины зоны перекрытия ранговых интервалов в совокупности с расчетными значениями обеспечивает повышение достоверности выводов и снижает вероятность ошибок при проверке статистических гипотез.



