Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Головной мозг, как и любой другой физический объект, имеет набор определенных характеристик, присущих ему и его изменению в пространстве. Сложность описания головного мозга как физического объекта состоит в его неклассическом поведении, главным образом это выражается в нехарактерной для других объектов деформации структур.

Деформация мозга непосредственно связана с изменением локализации структурных компонентов мозга – их дислокацией. Дислокация мозговых структур может возникать из-за наличия быстрорастущего опухолевого поражения [1]. Изменение мозговых структур при наличии объемного образования устанавливается с помощью предоперационной МРТ [2]. Дислокация мозговых структур возникает не только по причине наличия новообразования, но и из-за деформации, возникающей в ходе самой операции на головном мозге: при трепанации целостность пространства нарушается, а внутричерепное давление меняется на атмосферное.

Вследствие изменения давления происходит дислокация всех структур [3]. Фактическое положение тканей и определенные границы опухолевого процесса во время операции не совпадают с теми, которые отражены на предоперационных МРТ изображениях. Это снижает предсказуемость выполнения операции по удалению опухоли для нейрохирурга и затрудняет тотальное удаление опухоли, что, в свою очередь, может стать причиной образования рецидива опухоли или появления неврологических отклонений.

Для решения вышеуказанных проблем мы предлагаем использование подхода, основанного на применении моделирования деформации, который визуализирует изменения в головном мозге во время операции. В основе данного метода лежат математические и статистические принципы прогнозирования, созданные на основе теории механики сплошных сред с применением численных методов решения. Целью моделирования является выяснение механизмов взаимодействия элементов системы, идентификация параметров модели и прогноз поведения системы при различных внешних воздействиях.

Предлагаем рассмотреть применимые методы моделирования деформации с четырех уровней: физического, математического, уровня вычислительных алгоритмов и метода регистрации параметров:

− физический уровень (ФУ) – установление физических процессов и допущений, применяемых для головного мозга;

− математический уровень (МУ) – описание математического аппарата по предложенному физическому уровню;

− уровень подбора параметров (УПП) – задание или считывание параметров, необходимых для решения математических подходов;

− вычислительный уровень (ВУ) – разработка программ, визуализирующих деформацию, согласно математическим преобразованиям.

Использование подходов, основанных на применении моделирования деформации, потенциально может стать незаменимым инструментом в планировании операций по удалению глиальных опухолей головного мозга. Но не все модели деформации равнозначно могут быть использованы, в связи с возможными расхождениями между наблюдаемым объектом и результатами моделирования. Возможность таких расхождений требует проведения анализа моделей деформации, на основе которого будут выявлены недостатки современных инструментов, ограничивающих их применимость.

В соответствии с вышесказанным нами был введен ряд критериев для каждого уровня, согласно которому производился отбор и анализ моделей:

− критерии физического уровня:

1) учет анизотропии тканей. Необходим учет различия механических свойств головного мозга в зависимости от направления;

2) учет несжимаемых компонентов. Модель должна учитывать наличие несжимаемых жидкостных компонентов, входящих в головной мозг;

3) учет вязкоупругости тканей. В вязкоупругих тканях напряженно-деформированное состояние в определенный момент времени связано с предшествующими значениями напряжений и деформаций; в модели должен быть учет данного свойства;

4) учет физической и геометрической нелинейности. Связь напряжение – деформация в модели должна быть нелинейной;

5) устойчивость к большим деформациям. Материал мозга принимается как эластомер, который способен выдерживать большие деформации. В модели должно быть это отражено;

6) гибридность модели. Необходим учет различных структурных компонентов головного мозга и их физических свойств;

− критерии математического уровня:

1) нелинейность модели. Все математические выражения должны учитывать нелинейное поведение головного мозга;

2) решаемость при заданных граничных условиях. Граничные условия, выставляемые в физическом уровне и уровне подбора параметров, должны обеспечивать решаемость математических выражений;

− критерии вычислительного уровня:

1) возможность изменения геометрии модели. Модель должна строиться на основе МРТ снимков конкретного пациента;

2) 3D моделирование. Должна быть построена 3D модель головного мозга на основе данных из МР-изображений для обеспечения наибольшей точности проектирования деформаций;

3) моделирование производится в реальном времени. Осуществление моделирования должно происходить с минимальной затратой времени на обработку информации и работу программы;

− критерии подбора параметров:

1) получение данных из МРТ снимков. Для подбора параметров в модели должны быть использованы данные со снимков конкретного пациента;

2) моделирование производится в реальном времени. Подбор параметров должен происходить с минимальной затратой времени на обработку данных и работу программы.

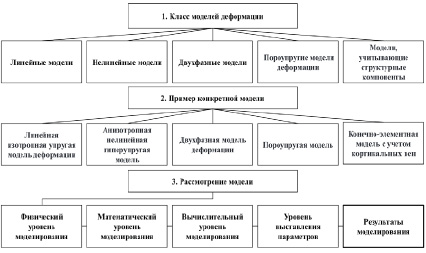
Структурная схема обзора моделей деформации

Целью настоящего исследования является обзор методов учёта деформации головного мозга и оценка их эффективности.

В данной работе рассматриваются пять классов моделей деформации и конкретные примеры для каждого класса моделей. Структура обзора представлена на рисунке.

1. Линейные модели деформации

Базовой моделью считается линейная модель упругой среды [4].

Линейная изотропная упругая модель деформации

Наиболее частым считается допущение об изотропной среде, упругие свойства которой не зависят от направления. В качестве конкретного примера рассмотрим линейную изотропную упругую модель [5].

1. Физический уровень

В процессе моделирования происходит различие двух материалов: мозговая ткань и кости черепа.

Допущения модели:

1) биологический материал принимается как упругий и изотропный;

2) деформация задаётся на поверхности мозга;

3) напряжение устанавливается находящимся в линейной зависимости от деформаций;

4) нагружение считается статическим;

5) предполагается, что в мозге происходит малая деформация.

2. Математический уровень

Уравнение для описания поведения материала в данном исследовании принимает вид

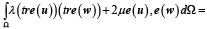
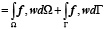(1)

где λ и μ – константы Ламе, u – неизвестное векторное поле смещения, e(·) – малый тензор деформаций Коши, f – приложенные силы, w – произвольная весовая функция и (tr · ) след матрицы.

3. Вычислительный уровень

Для моделирования деформаций в головном мозге в [5] были использованы предоперационные 2D МР-изображения (34 снимка). Реализация производилась в среде программирования конечных элементов DIFFPACK. Моделирование включало различные типы движений (перемещение, вращение) и аффинные преобразования (масштабирование, сдвиг) жесткого объекта, встроенного в эластичный материал. Для качественной оценки моделирования деформаций головного мозга производилось сравнение с послеоперационным изображением.

4. Параметры в линейной изотропной упругой модели деформации

Для определения параметров в модели [5] использовалось соотношение коэффициентов Ламе λ/µ различных структурных компонентов (череп и вещество мозга), подобранное путём усреднения уже известных из литературы констант. Для достижения наибольшей достоверности моделирования авторами были выбраны соотношения с определенной точностью; значения представлены в табл. 1.

Таблица 1

Параметры в линейной изотропной упругой модели деформации

Результаты моделирования

По данным исследователей [5] описанный теоретический эксперимент достоверно предсказывает изменения мозга в закрытом пространстве, но при наблюдении интраоперационных изменений отмечается несостоятельность метода и значительные различия между реальным поведением головного мозга во время операции и результатами авторов. Ввиду вышеуказанных фактов, в предоперационной подготовке неэффективен.

2. Нелинейные модели деформации

Следующий класс моделей – нелинейные модели деформации, которые принимают ткань моделируемого объекта как гиперупругую.

Анизотропная нелинейная гиперупругая модель

1. Физический уровень

В модели [6] рассматривалось биологическое вещество как гиперупругий материал, поведение которого с точки зрения механики деформируемого тела можно описывать нелинейными законами связи напряжение – деформация.

Для описания напряженно-деформированного состояния гиперупругих материалов необходимо выразить связь напряжений и деформаций через одну характеристику, которая бы не имела зависимости от деформаций [7].

Данная модель используется для описания материалов, которые способны выдерживать большие восстанавливающие упругие деформации [6].

Допущения модели:

1) предполагается, что материал должен состоять из нескольких изотропных веществ, которые образуют анизотропный композитный материал;

2) устанавливается нелинейная связь между напряжениями и деформациями;

3) биологический материал принимается как упругий.

2. Математический уровень

Для описания поведения мягких биологических тканей, согласно исследователям [8], используется гиперупругая функция Огдена, которая определяется как

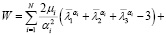
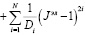(2)

где μi – параметр Огдена соответствующего вещества (измеряемый в Па), αi – параметр материала, 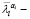девиаторные основные направления (равные 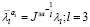), Di –параметр материала (измеряемый в Па-1), Jэл – объемная деформация элемента (эквивалентная λ1λ2λ3), N – количество веществ.

3. Вычислительный уровень

В исследовании для моделирования использовался специальный пакет ABAQUS для метода конечных элементов. Большое влияние на время работы метода доставляют структурные неоднородности, такие как волнистость аксона. Моделирование деформации мозга ограничивается небольшим участком, принимая, что поведение всего мозга такое же, как на участке.

4. Параметры в нелинейной анизотропной гиперупругой модели деформации

Для параметров в [6] использовалось исследование, в котором оптические нервы морских свинок сравнивали с аксонами.

Утверждается, что оптический нерв человека имеет схожее строение с нервом морской свинки. Исследованные ранее значения для морской свинки были представлены в работе [6]. Также принимается, что аксоны в три раза жестче, чем окружающая их ткань. Все данные представлены в табл. 2.

Таблица 2

Параметры в нелинейной анизотропной гиперупругой модели деформации

Результаты моделирования

Данная модель оценивала изменения отдельной части мозга – аксона в белом веществе, моделирование всего мозга в совокупности не проводилось. В представленном виде модель малоинформативна из-за рассмотрения лишь одной структурной компоненты.

3. Двухфазные модели деформации

Для класса двухфазных моделей деформации характерен учет различных фаз, содержащихся в веществе мозга.

Двухфазная модель деформаций

1. Физический уровень

Рассмотрим двухфазную модель деформаций [8]. В методе происходит учет дуральных перегородок, путем сегментации отдельных областей мозга. При моделировании производится учет двух видов деформаций: деформации, вызванной силой тяжести, и деформации, вызываемой маннитом, гиперосмолярным препаратом, вводимым перед операцией для снижения внутричерепного давления.

Допущения модели:

1) предполагается учет дуральных перегородок, как составной части мозга;

2) не производится учет различия биомеханических свойств структур мозга.

2. Математический уровень

Уравнения двухфазной консолидации, использованные в работе [8]:

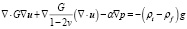, (3)

где u – вектор смещения, p – внутритканевое давление (измеряемое в Па), G – модуль сдвига, v – коэффициент Пуассона, α – отношение объема извлеченной жидкости к изменению объема ткани при сжатии, ρt – плотность ткани (измеряемая в кг/м3), ρf – плотность жидкости (измеряемая в кг/м3), g – гравитационная постоянная (измеряемая в м/с2).

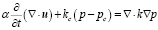, (4)

где t – время (измеряемое в с), kc – проницаемость капилляров, pc – внутрикапиллярное давление (измеряемое в Па), k – гидравлическая проводимость (измеряемая в м3с/кг).

3. Вычислительный уровень

Для моделирования деформаций по полученным до операции МР-изображениям вручную исследователями была построена конечно-элементная сетка, которая затем преобразовалась в сетку интенсивности. В работе использовалось более 60 положений головы для создания трехмерного представления деформаций головного мозга.

4. Параметры в двухфазной модели деформации

Свойства материалов в модели [8], представленные в табл. 3, основаны на ранее известных константах из литературы, а также на параметрах, полученных путем оптимизации в экспериментах по разработке и количественной оценке трехмерной модели деформации головного мозга для стереотаксической нейрохирургии, которые проводились на основе данных из предоперационных МРТ-изображений.

Таблица 3

Параметры в двухфазной модели деформации

Также были введены дополнительные параметры: коэффициент Пуассона v = 0,45; плотность ткани и жидкости ρt,f = 1000 кг/м3; внутрикапиллярное давление pc = 3633 Па; гравитационная постоянная g = 9,81 м/с2; отношение объема извлеченной жидкости к изменению объема ткани при сжатии α = 1.

Результаты моделирования

В исследовании [8] была проведена визуализация деформаций мозга по предоперационным МР-изображения. При сравнении работы модели и интраоперационных снимков наблюдается гораздо больше динамических взаимодействий, чем предполагали авторы. Границы опухоли, полученные в результатах, не могли обеспечить радикальность резекции.

4. Пороупругие модели деформации

Как известно, дальнейшие процессы моделирования деформаций включали в себя условия о пороупругом поведении среды.

Пороупругая модель

В последующем развитии теории биофизики было установлено, что модели деформации должны учитывать свойство пороупругости.

1. Физический уровень

В теории о пороупругости рассматривается математическая модель Био для описания деформации пористого материала, содержащего вязкие жидкости.

По данным [9], в мягких биологических тканях значения упругих модулей твердой матицы и внутритканевой жидкости достаточно близки, что приводит к необходимости учета жидкой фазы не только в динамике, но и при статическом нагружении.

Допущения модели:

1) предполагается, что ликвор абсорбируется, когда просачивается из ткани в область субарахноидального пространства;

2) материал мозга принимается изотропным и пороэластичным;

3) амплитуда давления жидкости в каналах увеличивается линейно с увеличением частоты нагрузки, может достигать уровня нескольких паскалей.

2. Математический уровень

В рассматриваемой модели используются константы Ламе, которые вычисляются через модуль Юнга E и коэффициент Пуассона v:

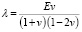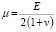и . (5)

Балансировка прихода и расхода удовлетворяет выражению

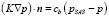, (6)

где K = k / μf – гидравлическая проводимость, k – гидравлическая проницаемость (k > 0), μf – вязкость жидкости (измеряемая в Па∙с), p – давление жидкой фазы (измеряемое в Па), pSAS – давление спинномозгового канала (измеряемое в Па).

Проводимость cb была рассчитана как

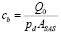. (7)

Неоднородность мозга (желудочки) представляет из себя только жидкую фазу. Тем самым в модели учет данной структуры был произведен в виде жидкости:

(σ – αp) · n = –p · n, (8)

где σ – тензор напряжений, α – коэффициент Био-Уиллиса (близкий к 1).

3. Вычислительный уровень

Для создания модели было выбрано 2D поперечное сечение 3D модели, из которого были получены геометрические размеры для построения сетки конечных элементов при помощи программного обеспечения GMSH.

4. Параметры в пороупругой модели деформации

В работе [9] для установления значений параметров проводились серии экспериментов, в ходе которых в решение уравнений (5), (6) и (8) подставлялись определенные значения, а затем путем сравнения выбирались наиболее подходящие, например модуль Юнга E и гидравлическая проницаемость мозга k.

В ходе моделирования происходило сравнение с опытными данными, принятыми базовыми, они представлены в табл. 4.

Результаты моделирования

Исследование [9] направлено на установление максимальных напряжений в головном мозге, МРТ визуализация деформации на основе предоперационных снимков не проводилась. Также в рамках данной работы была произведена иллюстрация напряжённого состояния ткани мозга около опухоли. В рамках предоперационного планирования модель может быть использована как составной компонент инструмента; в представленном виде явно применяться для планирования резекции не может.

5. Модели деформации, учитывающие структурные компоненты

В рамках данного класса учитываются различия структурных компонентов. Так, предполагает, что жидкостям соответствуют вязкие модели, серому и белому веществу – пороупругие модели с учетом вязкости, а твердым оболочкам мозга и черепу необходимы модели для твердых тканей.

Конечно-элементная модель с учетом кортикальных вен

В данном классе моделей рассматривается исследование [10], в котором осуществлялся учет кортикальных сосудов головного мозга.

1. Физический уровень

Несмотря на наличие учета неоднородности мозговых структур, рассматриваемая модель не вносит новизну в описание деформации всего мозга, принимая поведение других компонентов линейным.

Таблица 4

Параметры в пороупругой модели деформации

2. Математический уровень

Допущения модели:

1) учитываются корковые сосуды;

2) используется линейная зависимость напряжений от деформаций.

Описано, что для работы всей модели необходимо было найти функцию преобразования Ф таким образом, чтобы

U = Ф(П,R,t,δu)(V),

где П – матрица камеры, которая конвертировала бы координаты камеры в координаты реального масштаба, R – вращение камеры, t – перенос матрицы, δu – нежесткий компонент преобразования и V – осевые линии.

Обратим внимание, что в данном инструменте записано уравнение, связывающее внешние силы f с узловыми смещениями x, представленное в виде

f = K(x)δx. (9)

3. Вычислительный уровень

В ходе исследования происходила разработка выражения для минимизации энергии биомеханической модели, которое содержало два слагаемых, первое из которых определяло физическую стойкость, а второе – подгонку изображений:

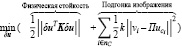, (10)

где k – коэффициент жесткости, связывающий исходную и целевую осевые линии для осуществления вычисления энергии изгиба.

В рассматриваемой модели исследователями применялся сосудистый метод регистрации дооперационных сканирований на интраоперационных изображениях, полученных с помощью хирургического микроскопа. Деформация рассчитана с использованием нелинейного геометрического метода конечных элементов.

4. Параметры в конечно-элементной модели с учетом кортикальных вен

Матрица жесткости строилась с модулем Юнга E, равным 3000 Па, и коэффициентом Пуассона, равным 0,45. Таким образом, для моделирования использовались опытные данные других исследователей, а интраоперационное изображение было использовано для регистрации размеров сосудов (данные в работе [10] не представлены).

Результаты моделирования

В данной работе производилась визуализация изменения положения головного мозга с опухолевым поражением на основе изображений кортикальных сосудов. В рамках предоперационной подготовки применение данной модели ограничено невозможностью визуализации глубинных структур головного мозга.

Оценка эффективности моделей по критериям

Оценка эффективности моделей проводилась по методу анализа иерархий Томаса Саати [11]. Конечные результаты представлены в табл. 5. Стоит отметить, что всем уровням моделирования было присвоено сокращение.

Проведенный аналитический обзор моделей деформаций головного мозга показал, что двухфазная модель имеет наибольшее соответствие выставленным критериям, что указывает на эффективность данной модели относительно ранее указанной медицинской проблемы. Ограниченность применения этой модели в качестве средства предоперационной визуализации деформаций головного мозга обусловлена ошибкой порядка нескольких миллиметров между результатами моделирования и интраоперационной картиной.

Таблица 5

Оценка моделей деформации по критериям

Условием выбора наиболее эффективной для предоперационного планирования модели деформации являлось полное соответствие выставленным критериям. Данное условие не было выполнено ни для одной из рассмотренных моделей. Также в ходе анализа установлено, что критерии физического уровня совсем не выполняются; это говорит о недостаточном развитии теории о головном мозге как физическом объекте.

Согласно вышесказанному использование моделей, учитывающих только одно определенное свойство, такое как нелинейность или пороупругость, не даёт заявленной точности в визуализации интраоперационных изменений головного мозга. Соответственно, создание модели, объединяющей несколько из рассмотренных, позволит решить актуальную проблему нейрохирургии.

Таким образом, ни одна из представленных моделей не является эффективной для решения проблемы затруднения тотальной резекции опухоли из-за деформации головного мозга во время операции. Дальнейшее развитие инструментов моделирования, заключающееся в комбинировании нескольких из рассмотренных моделей, а также углублении в физическую теорию предметной области, позволит создать средство информационной поддержки для нейрохирургов, которое бы с точностью визуализировало интраоперационную деформацию мозга, что поможет увеличить выживаемость пациентов.