Применяемые на практике для крупнотоннажных производств биореакторы характеризуются большим геометрическим объемом (порядка 100–1000 м3), но относительно невысокой удельной производительностью процессов ферментации по целевому продукту и низким массообменом кислорода при больших мощностях предприятия в целом [1]. Имеющееся при этом различие в массообменных характеристиках по зонам аппарата и проявление неидеальных по объему аппарата условий перемешивания оказывают влияние на качественное снабжение ферментационной среды кислородом. Устранение возникающих в таких условиях большого перерегулирования и длительных отклонений концентрации растворенного в ферментационной среде кислорода (рО2) от оптимального значения с использованием подачи больших объемов воздуха на аэрацию не всегда эффективно. Процессы, протекающие в контуре подачи воздуха в аппараты, реализуются с помощью компрессоров, приводимых в действие асинхронными электродвигателями. Для регулирования скорости асинхронных электродвигателей с короткозамкнутым ротором применяют преобразователи частоты. На преобразователь частоты подается управляющий сигнал, который задает режимы работы электродвигателя и компрессора. Неэффективное управляющее воздействие может быть причиной автоколебательного режима работы компрессора и, как следствие, причиной колебаний давления и расхода воздуха. Такой режим приводит к завышенным объемам подаваемого воздуха и ведет к неоправданному перерасходу электроэнергии. Для устранения этого требуется применение эффективной системы автоматического управления (САУ) подачей аэрирующего воздуха, отрабатывающей переменные задающие воздействия и возмущения без существенных перерегулирований и максимальных динамических отклонений регулируемой переменной рО2 с приемлемыми временем нарастания в переходном режиме и точностью в установившемся режиме. С учетом изложенного усовершенствование САУ режимом аэрации при реализации оптимальной программы подачи воздуха в аппарат является важной для аэробных процессов, основанных на микробиологическом синтезе, так как современные биотехнологии лежат в основе получения продукции пищевых, химико-фармацевтических и сельскохозяйственных производств. Многорежимность и неопределенность условий функционирования обуславливают необходимость решения задачи синтеза САУ с использованием методов интеллектуальной технологии, например нечеткой логики. Универсальные методы решения задач синтеза многорежимных систем управления процессами аэрации на основе методов нечеткой логики в настоящее время отсутствуют. Поэтому задача разработки и исследования интеллектуальной многорежимной системы управления режимом аэрации биотехнологическими объектами различного назначения является актуальной.
Целью исследования является повышение эффективности управления режимом аэрации с помощью разработки многорежимной системы управления на основе регулятора стабилизации расхода воздуха на аэрацию и регулятора концентрации растворенного кислорода с аппроксимирующим законом управления и коррекцией его параметров в переходном и установившемся режимах с помощью нечеткой логики.
Анализ особенностей структуры системы управления и методы исследования
Свойства процесса биосинтеза, протекающего в биореакторах периодического действия, таковы, что оптимальный режим аэрации, обеспечивающий необходимый уровень концентрации растворенного в среде кислорода, не может быть реализован подачей постоянного расхода воздуха в аппарат. Это подтверждается, с одной стороны, необходимостью реализации оптимального профиля расхода воздуха на аэрацию, а с другой стороны, обусловлено многорежимностью процесса [2]: наличием режима адаптации (режима приспособления культуры микроорганизмов к условиям среды после ее загрузки в аппарат), режима неустановившегося роста биомассы, режима интенсивного продуктообразования, режима стабилизации и замедления роста микроорганизмов. Характер этих режимов зависит от физиологического состояния микроорганизмов и различных факторов среды, среди которых одним из основных является концентрация растворенного кислорода. В связи с этим управление биореакторами, функционирующими в широком диапазоне переходных и установившихся режимов, требует многорежимных систем управления (МСУ) на основе автоматических регуляторов стабилизации воздуха с коррекцией по рО2 различной сложности по структуре и алгоритму в зависимости от требования точности поддержания заданного режима. В данной работе в корректирующем контуре применен фаззи-регулятор с аппроксимирующим управлением (РАУ), имеющий уравнение вида [3]:
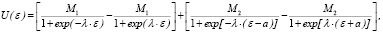 (1)
(1)
где М1, М2 – параметры настройки, определяющие величину корректирующего воздействия в зоне нечувствительности (ЗН) и за её пределами соответственно; ε – ошибка регулирования; λ – параметр настройки, определяющий наклон линейного участка аппроксимирующей характеристики; а – половина ЗН.
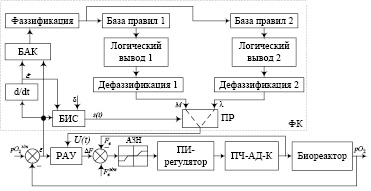
Рис. 1. САУ подачей воздуха на аэрацию с коррекцией по рО2:
ФК – фаззи-корректор; РАУ – регулятор с аппроксимирующим управлением; БАК – блок анализа качества системы; ПР – переключающее реле; δ – сигнал, определяющий условие переключения ПР; АЗН – аппроксимированная зона нечувствительности; БИС – блок изменения структуры; ПЧ-АД-К – соответственно преобразователь частоты (ПЧ), асинхронный двигатель (АД), компрессор (К)
Структурная схема интеллектуальной САУ с нечеткой логикой представлена на рис. 1 [4].
В блоке изменения структуры (БИС) формируется командный сигнал, поступающий на вход переключающего реле (ПР), который изменяет структуру системы, подключая на вход РАУ воздействие Uк(t) с выхода фаззи-корректора (ФК) в соответствии с алгоритмом функционирования:
если S(t) > δ , то Uк1(t)=М;
если S(t) < δ , то Uк2(t)=λ, (2)
где
S(t) = ε(t) + Tоб · 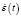 ;
;
ε(t), 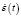 – сигнал рассогласования и его производная; Тоб – постоянная времени хвостового участка переходной функции объекта; δ – положительный параметр, задающий размер «переходной» области от пускового (переходного) режима к установившемуся (δ = const); Uк1(t), Uк2(t) – корректирующее воздействие первого и второго фаззи-блока соответственно; М, λ – параметры настройки РАУ; М1 = М, М2 = к∙М, к – коэффициент пропорциональности, задаваемый априори.
– сигнал рассогласования и его производная; Тоб – постоянная времени хвостового участка переходной функции объекта; δ – положительный параметр, задающий размер «переходной» области от пускового (переходного) режима к установившемуся (δ = const); Uк1(t), Uк2(t) – корректирующее воздействие первого и второго фаззи-блока соответственно; М, λ – параметры настройки РАУ; М1 = М, М2 = к∙М, к – коэффициент пропорциональности, задаваемый априори.
Приведенный алгоритм (2) функционирования БИС обеспечивает адаптацию управления к режимам функционирования в условиях неопределенности следующим образом: в контуре управления режимом аэрации воздействие внутреннего регулятора поступает на вход объекта, обеспечивая заданное значение расхода воздуха на аэрацию. При изменении концентрации рО2 на вход фаззи-корректоров поступает ошибка регулирования и ее производная. В соответствии с (2) формируется корректирующее воздействие на параметры РАУ, например М1 = М, М2 = к∙М при λ = const в переходном режиме или λ = var при М = const в установившемся режиме. За счет этого реализуется поправка к задаваемому значению расхода воздуха на аэрацию, улучшая при этом динамику процесса в переходном и установившемся режимах.
Подача расхода воздуха осуществляется с помощью нечеткого корректирующего регулятора с аппроксимирующим управлением с коррекцией по рО2 в биореакторе. Использование нечеткого регулятора дает возможность проектировать САУ, способные эффективно функционировать при наличии информации об объекте управления лишь качественного характера [5]. Вместе с тем, несмотря на интенсивные исследования в области применения методов нечеткой логики в системах управления, все еще остаются не полностью решенными многие проблемы, связанные с разработкой методики синтеза и анализа рассматриваемых многорежимных систем. В частности, в большинстве работ по управлению многорежимными системами не рассмотрена возможность применения регуляторов с аппроксимирующим управлением и построения нечетких регуляторов на их основе.
Типовыми режимами многих САУ являются установившиеся и переходные режимы. В установившемся режиме всегда есть возмущения параметров ее режима, при которых она должна быть устойчива и обладать в достаточной мере помехозащищенностью. В переходном режиме основной задачей является обеспечение приемлемого времени нарастания и недопущение значительного перерегулирования и максимальных динамических отклонений при переходе к установившемуся режиму. С учетом этого исследование переходных процессов в МСУ проведено при различных внешних возмущениях. При этом учтено, что при изменении режима аэрации для оценки запаса устойчивости в системе при вариациях ее параметров, проводится анализ переходных процессов, когда возмущение воздействует на вход объекта. При анализе качества регулирования при изменении задающего воздействия на регулятор расхода воздуха на аэрацию и непредсказуемом действии внешних возмущений на входе объекта проводится анализ переходных процессов при одновременном действии этих воздействий. Для оценки качества регулирования в установившемся режиме проводится анализ переходных процессов, когда после вывода на режим возмущения действуют по каналу регулирования рО2 в различные моменты времени.
С использованием интервалов квазистационарности процесса ферментации получены графики переходных процессов для четырех режимов функционирования системы:
режим 1 – вывод объекта на заданный режим с последующей стабилизацией рО2 при ступенчатых изменениях сигнала задания регулятору расхода воздуха на аэрацию Fздн = 10 м.е., сигнала задания по рО2 корректирующего контура рО2здн = 5 м.е. (м.е. – машинные единицы) и случайного сигнала помехи с нормальным распределением уровня сигнала, имеющего дисперсию D = 0,01 на входе регулятора расхода воздуха на аэрацию при t = 0;
режим 2 – стабилизация рО2 при ступенчатых изменениях сигнала задания регулятору расхода воздуха на аэрацию Fздн = 13 м.е., сигнала задания по рО2 корректирующего контура рО2здн = 5 м.е. (м.е. – машинные единицы) и сигнала помехи, имеющей дисперсию D = 0,01, на входе регулятора расхода воздуха на аэрацию при 150 ≤ t < 300 мин;
режим 3 – стабилизация рО2 при ступенчатых изменениях сигнала задания регулятору расхода воздуха на аэрацию Fздн = 28 м.е., сигнала задания по рО2 корректирующего контура рО2здн = 5 м.е. (м.е. – машинные единицы) и сигнала помехи, имеющей дисперсию D = 0,01, на входе регулятора расхода воздуха на аэрацию при 300 ≤ t < 550 мин;
режим 4 – стабилизация рО2 при ступенчатых изменениях сигнала задания регулятору расхода воздуха на аэрацию Fздн = 8 м.е., сигнала задания по рО2 корректирующего контура рО2здн = 5 м.е. (м.е. – машинные единицы) и сигнала помехи, имеющей дисперсию D = 0,01, на входе регулятора расхода воздуха на аэрацию при t = 550 мин.
Изменение сигнала задания регулятору расхода воздуха на аэрацию осуществлено по закону
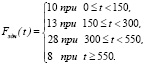 (3)
(3)
Заданное значение расхода воздуха на аэрацию в данной системе определяется выражением
Fвздн = Fвопт + ΔFв ,
где Fвопт – задание оптимального расхода воздуха, определяемое как результат решения задачи оптимизации; ΔFв – поправка расхода воздуха, формируемая фаззи-регулятором с аппроксимирующим управлением по результатам измерения отклонений содержания растворенного кислорода в среде культивирования.
Отклонение расхода воздуха, подаваемого в биореактор, с учетом содержания растворенного кислорода в среде определяется из выражения
ΔF = Fвздн – Fв ,
где Fв – текущее значение расхода воздуха на аэрацию.
Синтез регулятора с аппроксимирующим управлением (РАУ) в системе управления концентрацией рО2 осуществлен с использованием модели объекта по каналу регулирования «расход воздуха на аэрацию – концентрация рО2» в следующем виде:
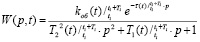 ,
,
где 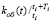 – коэффициент передачи объекта;
– коэффициент передачи объекта;
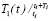 ,
, 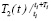 – постоянные времени объекта;
– постоянные времени объекта;
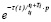 – время запаздывания;
– время запаздывания;
ti – аргумент времени (независимая переменная);
р – комплексная переменная;
Тi – интервалы квазистационарности (i = 1, 2, 3, 4, 5), длительность которых достаточна для фаззи-коррекции параметров РАУ.
Наличие интервалов квазистационарности процесса позволило перейти от параметрических передаточных функций W(p,t), в которых аргумент t рассматривается как параметр, к передаточным функциям Wi(p) с постоянными коэффициентами для моментов времени ti (i = 1…5) или для интервалов времени квазистационарности [0 … Ti]. Если параметры передаточной функции являются медленно меняющимися функциями в интервале времени, то можно считать параметры передаточной функции Wi(p) постоянными в этом интервале и использовать ее для моделирования системы. Для такого случая модель можно записать в следующем виде:
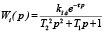 , (i = 1…5)
, (i = 1…5)
где kоб – коэффициент передачи,
0,097 ≤ kоб ≤ 0,275, %/м3/ч;
τ – запаздывание объекта, 2 ≤ τ ≤ 5,7, мин;
T1 , T2 – постоянные времени объекта, 7,83 ≤ T1 ≤ 14,8, мин; 4,61 ≤ T2 ≤ 10,08, мин.
Используя граничные значения параметров модели, можно получить интервальную модель многорежимного объекта для анализа и синтеза многорежимной системы управления. Интервальная модель объекта по каналу «расход воздуха на аэрацию – концентрация рО2» реализована в следующем виде:
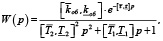
где 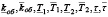 – нижняя и верхняя границы коэффициента передачи объекта kоб, постоянной времени Т1, Т2 и запаздывания объекта τ соответственно.
– нижняя и верхняя границы коэффициента передачи объекта kоб, постоянной времени Т1, Т2 и запаздывания объекта τ соответственно.
При наличии интервальной модели, следуя [6], можно определить параметры номинальной (расчетной) модели для объекта с параметрической неопределенностью как модели, которая находится в центре множества. В этом случае значения параметров номинальной модели объекта рассчитываются как среднеинтервальные:
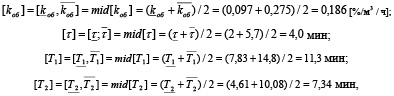
где mid[vi] – среднее значение параметра модели объекта [vi], i = 1,…,4.
Результаты исследования и их обсуждение
На основе результатов проведенных исследований установлено, что в САУ режимом аэрации целесообразно использовать типовой регулятор стабилизации расхода воздуха на аэрацию, а корректирующий регулятор по концентрации рО2 в биореакторе (РАУ) рационально строить с использованием метода аппроксимирующих преобразований и коррекцией его параметров с помощью нечеткой логики. Для моделирования системы и проектирования фаззи-регулятора эффективно использованы возможности среды моделирования MATLAB Simulink, а также пакет нечеткой логики Fuzzy Logic Toolbox [7]. Полученные переходные процессы в САУ с фаззи-коррекцией коэффициентов М1 и М2 на интервалах квазистационарности процесса (i = 1, 2, 3, 4, 5), совмещенных с режимами – фазами физиологического развития микроорганизмов, представлены на рис. 2. Из рисунка видно, что использование РАУ с нечеткой коррекцией параметров закона управления не приводит к разрывным управлениям при смене режимов. Поверхность вывода корректирующего воздействия РАУ-регулятора представлена на рис. 2, е, из которого видно, что полученная трехмерная поверхность для нечеткого регулирования в переходном и установившемся режимах, содержащая значения переменных ε и dε/dt и корректируемого параметра М регулятора с аппроксимирующей функцией управления, является нелинейной.
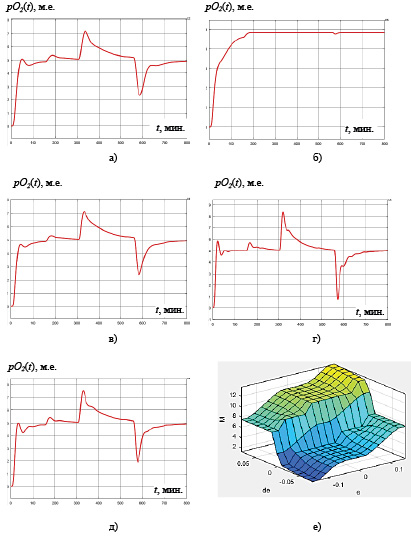
Рис. 2. Переходные процессы в САУ с фаззи-коррекцией коэффициентов М1 и М2 на интервалах квазистационарности – фазах процесса 1, 2, 3, 4 и 5 (а, б, в, г и д) соответственно и поверхность вывода корректирующего воздействия РАУ-регулятора (е)
Кривизна поверхности в области требуемых значений корректируемого параметра свидетельствует о значимости данного параметра для соответствующих режимов и достаточности выбранных функций принадлежности, определяющих связь входных и выходных переменных с лингвистическими. Значения показателей качества переходных процессов приведены в таблице.
Показатели качества переходных процессов в исследуемых режимах (при фаззи-коррекции / при отсутствии коррекции параметров)
|
Показатели качества переходного процесса |
Режим 1 |
Режим 2 |
Режим 3 |
Режим 4 |
|
Режим (фаза) адаптации, интервал квазистационарности процесса [0 ÷ 11,25] час, модель объекта |
||||
|
Время нарастания Тн, мин |
37,5*/28.75 |
–/– |
–/– |
–/– |
|
Перерегулирование σ, % |
–/18 |
–/– |
–/– |
–/– |
|
Максимальное отклонение Аmax, м. ед. |
–/0,9 |
0,4/0,3* |
2/1,8* |
2,4/2* |
|
Время переходного процесса Т, мин |
150/162,5 |
100/125 |
250/350 |
225/300 |
|
Режим (фаза) ускорения роста, интервал квазистационарности процесса [11,25 ÷ 33,75] час, модель объекта |
||||
|
Время нарастания Тн, мин |
162,5*/250* |
–/– |
–/– |
–/– |
|
Перерегулирование σ, % |
–/– |
–/– |
–/– |
–/– |
|
Максимальное отклонение Аmax, м. ед. |
–/– |
0,18/0,3 |
1,27/1,0 |
1,45/1,6 |
|
Время переходного процесса Т, мин |
107,5/300 |
50/187,5 |
250/350 |
162,5/200 |
|
Режим (фаза) экспоненциального роста, интервал квазистационарности процесса [33,75 ÷ 67,5] час, модель объекта |
||||
|
Время нарастания Тн, мин |
162,5*/26,3** |
–/– |
–/– |
–/– |
|
Перерегулирование σ, % |
–/12 |
–/– |
–/– |
–/– |
|
Максимальное отклонение Аmax, м. ед. |
–/0,6 |
0,18/0,2 |
2,0/1,8 |
2,5/2 |
|
Время переходного процесса Т, мин |
150/175 |
130/150 |
250/350 |
220/250 |
|
Режим (фаза) замедления роста, интервал квазистационарности процесса [67,5 ÷ 118,75] час, модель объекта |
||||
|
Время нарастания Тн, мин |
12,5**/12,5 |
–/– |
–/– |
–/– |
|
Перерегулирование σ, % |
16/– |
–/– |
–/– |
–/– |
|
Максимальное отклонение Аmax, м. ед. |
0,2/3 |
0,75/1,7 |
3,2/2,2 |
4/3 |
|
Время переходного процесса Т, мин |
75/350 |
150/350 |
200/350 |
250/350 |
|
Режим (фаза) стационарного роста, интервал квазистационарности процесса [118,75 ÷ 130,0] час, модель объекта |
||||
|
Время нарастания Тн, мин |
25*/18,75 |
–/– |
–/– |
–/– |
|
Перерегулирование σ, % |
–/26 |
–/– |
–/– |
–/– |
|
Максимальное отклонение Аmax, м.ед. |
–/1,3 |
0,27/0,3 |
2,5/2 |
3/2,4 |
|
Время переходного процесса Т, мин |
140/250 |
150/125 |
250/300 |
200/300 |
Примечания: * – апериодический характер переходного процесса;
** – колебательный характер переходного процесса.
Анализ показателей качества переходных процессов, приведенных в таблице, показал, что при фаззи-коррекции параметров М1 и М2 время нарастания в режиме 1 только для апериодических переходных процессов незначительно превышает время нарастания в случае отсутствия коррекции. Максимальное динамическое отклонение в режиме 2 во всех интервалах квазистационарности при коррекции меньше в 1,1–2,3 раза. Время переходного процесса при фаззи-коррекции за исключением интервала (118,75–136) часов также меньше в 1,2–3,8 раза. В режиме 3 максимальное отклонение при фаззи-коррекции незначительно, в 1,1–1,5, превышает максимальное динамическое отклонение Аmax при отсутствии коррекции. В режиме 4 максимальное динамическое отклонение Аmax при фаззи-коррекции в интервале (11,75–16,25) часов меньше в 1,1 раза, а при отсутствии фаззи-коррекции превышение незначительно и составляет в (1,2 – 1,3) раза больше. Во всех исследуемых интервалах время переходного процесса при фаззи-коррекции меньше в 1,1–4,7 раза.
Таким образом, с точки зрения быстродействия в разных режимах функционирования целесообразным следует считать управление с использованием коррекции параметров М1, М2 регулятора с аппроксимирующим управлением.
Заключение
Стремление к максимальному насыщению ферментационной среды кислородом за счет использования подачи воздуха на аэрацию приводит к неравномерному распределению концентрации растворенного кислорода в ферментационной среде. Результаты исследований показали, что обеспечение оптимальных условий насыщения среды кислородом возможно в многорежимной САУ подачей воздуха на аэрацию с коррекцией по концентрации растворенного кислорода в культуральной жидкости. Малое время нарастания в переходном (пусковом) режиме обеспечивается регулятором с аппроксимирующим управлением. При использовании данного регулятора упрощается процедура воздействия на параметры М1, М2, определяющие величину корректирующего воздействия в переходном режиме, исключая их избыточное влияние на качество переходных процессов в установившемся режиме. Наиболее простым алгоритмом такой коррекции является алгоритм на основе нечеткой логики. В результате достигается повышение эффективности за счет разработки и внедрения интеллектуальной системы управления с учетом всех возможных режимов работы объекта. Подтверждением этому являются полученные в данной работе результаты исследования разработанной многорежимной системы управления на основе комбинации принципов аппроксимирующего управления и нечеткой коррекции параметров алгоритма управления.




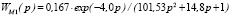 , %/м3/ч
, %/м3/ч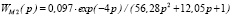 , %/м3/ч
, %/м3/ч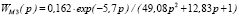 , %/м3/ч
, %/м3/ч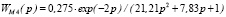 , %/м3/ч
, %/м3/ч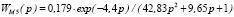 , %/м3/ч
, %/м3/ч