Проблемы, связанные с коррозией металла, являются одной из ключевых экономических и технических задач современности [1, 2]. Ряд отраслей, а в некоторых случаях даже экономики целых государств страдают из-за проблем, связанных с коррозией металла [3, 4]. Авторы работ [5, 6] указывают отрасли, в которых коррозионные задачи являются особо острыми. Среди таких отраслей особым образом выделяются промышленность, строительство и железнодорожная отрасль [7]. На железной дороге находится большое количество объектов инфраструктуры, подверженной коррозионным процессам. Крупные компании теряют миллиарды долларов из-за ущерба, связанного с коррозией металла. Проблемам предотвращения хаоса в процессах коррозии металлов посвящены работы [8, 9]. Тем не менее на сегодняшний день наблюдается острая нехватка прикладных разработок и практического применения теоретических аспектов коррозионной защиты, где фундаментальные исследования в довольно высокой мере опередили техническое применение [10]. Анализ вектора развития активных методов борьбы с коррозией металлов показывает, что одним из перспективных и экономически целесообразных путей борьбы с коррозией является применение современных информационных технологий, включая набор датчиков, АЦП/ЦАП-преобразователи, современные программные комплексы, основанные на эффективном использовании математических моделей и методов машинного обучения. Таким образом, разработка прикладных инструментов, направленных на решение коррозионных проблем, в частности на железнодорожном транспорте, является актуальной задачей.
Цель исследования заключается в разработке математических и компьютерных моделей, позволяющих исследовать коррозионные процессы металлов на объектах железнодорожной отрасли.
Материалы и методы исследования
Объектом исследования являются металлические конструкции, подверженные процессам коррозии, например объекты железнодорожной инфраструктуры. В качестве примера рассмотрена арматура пешеходного моста, проходящего над железнодорожными путями (рис. 1). Для моделирования коррозионных процессов рассмотрим металлическую пластину, помещенную в водный раствор.
На рис. 2 изображена схема процесса коррозии. В схеме используются следующие обозначения: МО – пленка оксида, МОН – пленка гидроксида, МОНр – растворенный гидроксид, МА – соль.
Для описания математической модели рассмотрим процесс электрохимической коррозии, при котором образуется пленка оксида металла и пленка гидроксида металла. Состояние системы можно описать с помощью положения точки в трехмерном фазовом пространстве μ0 – μОН – КМ [11], где μ0 – доля поверхности, покрытая оксидом металла, μОН – доля поверхности, покрытая гидроксидом металла, КМ – концентрация ионов металла в растворе. Для того чтобы рассчитать скорость изменения каждого из параметров, необходимо решить соответствующие кинетические уравнения и на основании полученных данных построить фазовые траектории движения фигуративной точки.

Рис. 1. Образец арматуры пешеходного моста
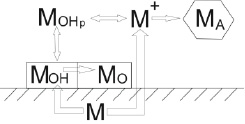
Рис. 2. Схема процесса коррозии
В качестве независимых переменных используем μ0, μОН, КМ, в качестве зависимой переменной μМ – доля поверхности непокрытого металла:
μМ = 1 – μ0, (1)
Запишем реакции, которые могут протекать на поверхности металла:
 (2)
(2)
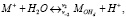 (3)
(3)
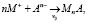 (4)
(4)
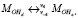 (5)
(5)
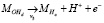 , (6)
, (6)
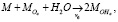 (7)
(7)
где An – растворенный анион, MnA – твердый осадок, v – константы скорости реакции. Индексы d, a указывают, что соответствующие виды частиц являются либо растворенными, либо адсорбированными соответственно.
В рассматриваемом случае An–, H2O и H+ присутствуют в избытке, а реакция (3) всегда находится в равновесии. Константы скорости в уравнении (4) представим в виде
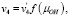 (8)
(8)
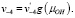 (9)
(9)
Принимая K = [M+], получим следующие дифференциальные уравнения для системы:
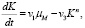 (10)
(10)
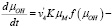
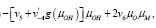 (11)
(11)
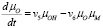 , (12)
, (12)
где μМ – доля оголенной металлической поверхности.
Введем в модель безразмерные переменные:
τ = v–4t , Z = VK (13)
и безразмерные параметры:
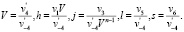 (14)
(14)
Таким образом, получим дифференциальные уравнения в безразмерных переменных:
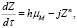 (15)
(15)
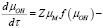
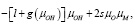 (16)
(16)
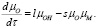 (17)
(17)
Уравнения (15)–(17) образуют систему связанных автономных нелинейных дифференциальных уравнений с тремя независимыми переменными состояния. Рассматривается случай однозарядного аниона и принимается, что f(μОН) = 1, g(μОН) = exp(–αμОН), где α – положительная безразмерная константа. Поскольку состояние системы описывается положением точки в трехмерном фазовом пространстве, т.е. в системе координат μ0 – μОН – КМ, то, решив систему нелинейных дифференциальных уравнений (15)–(17) и построив на основании полученных данных фазовую траекторию движения фигуративной точки, можно вычислить скорость изменения каждого из этих параметров. Таким образом, в качестве необходимых параметров для построения фазовых траекторий выбираем параметры μ0 – μОН – КМ.
Результаты исследования и их обсуждение
С помощью инструментов Zet Lab и языка программирования Python разработан программный комплекс, позволяющий решать необходимые кинетические уравнения и на основании полученных данных строить фазовые траектории. На рис. 3 изображена проекция фазовой траектории на плоскость μ0 – μОН, построенная в разработанном программном комплексе.
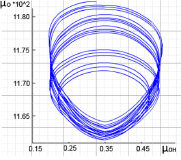
Рис. 3. Проекция фазовой траектории процесса коррозии на плоскость μ0 – μОН
Как видно из рисунка, траектория процесса коррозии представляет довольно сложную фигуру, имеющую хаотичную динамику. Важно найти порядок и закономерности в детерминированном хаосе и правильно отличить его от стохастического процесса. Автор работы [12] приводит процедуру, доказывающую, что траектория системы в правильно выбранном фазовом пространстве представляет собой странный аттрактор, а процесс коррозии может быть подавлен путем наложения на систему специально подобранных параметров, при которых аттрактор системы обращается в точку.
С помощью языка программирования Python разработан программный комплекс, реализующий метод возвратных карт, который применяется для построения фазовых траекторий на основании полученных данных. Подбирается промежуток времени τ, через который высота пиков коррозионного тока повторяется, а затем строится фазовая траектория в координатах I(t) – I(t+τ) (рис. 5).
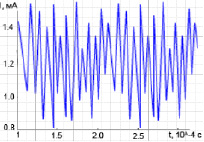
Рис. 4. График изменения коррозионного тока, полученный экспериментально
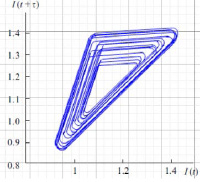
Рис. 5. Восстановление аттрактора по экспериментальной зависимости
Траекторией системы в правильно выбранном фазовом пространстве является странный аттрактор. Это свидетельствует о том, что коррозионный процесс содержит скрытый порядок, несмотря на то, что, на первый взгляд, ток коррозии меняется случайным образом.
Результаты моделирования показывают: чтобы подавить процесс коррозии, необходимо рассчитать параметры, при которых аттрактором системы станет точка.
Заключение
В результате исследований установлено, что фазовая траектория исследуемой системы является детерминированной. Это свидетельствует о том, что коррозионный процесс содержит скрытый порядок, несмотря на то, что, на первый взгляд, ток коррозии меняется случайным образом. Имеется возможность способствовать уменьшению коррозионных процессов за счет специально рассчитанных параметров внешнего воздействия. В качестве накладываемых на систему параметров можно использовать специально рассчитанный импульс напряжения. Результаты будут полезны при разработке прикладных средств для борьбы с коррозионными процессами.
Работа выполнена при поддержке ОАО «РЖД» грант № 4222988.



