Развитие в настоящее время имеют смежные с биологией науки, такие как биохимия, биофизика, потенциал у этих наук на данный момент очень велик, ведь существует множество вопросов, неописанных процессов и скрытых закономерностей.
Знание заряда и потенциала у поверхности мембраны весьма важно, так как это позволяет описывать процессы, связанные с транспортом ионов, адсорбцией заряженных частиц на мембранах, а также взаимодействие мембран. Обычно, чтобы получить распределение потенциала, необходимо знать структуру границы раздела «мембрана – раствор электролита», далее вычислить распределение заряда, и соответственно вычислить само распределение потенциала. Так как биологическая структура мембран очень сложна в описании, в силу огромного количества элементов, обычно используются упрощения. Часто в качестве модели границы раздела мембрана-раствор принимается модель, состоящая из двух полубесконечных сред: с одной стороны электролит, с другой жидкий диэлектрик.
В работе [1] для данного случая, при наличии точечного заряда в электролите, были получены формы распределения потенциала при наличии точечного заряда в электролите, но они громоздки и мало подходят для реальных случаев. Поэтому были получены приближенные формулы для произвольного количества фиксированных точечных зарядов, пригодные для качественной оценки и быстрых вычислений.
В работах [2; 3] приводились методики моделирования липидных бислоев. Наиболее распространенными методами моделирования являются:
а) методы молекулярной динамики (например, метод стохастической динамики). Данную группу методов обычно применяют, когда необходимо наблюдать и моделировать различные процессы, происходящие во времени;
б) метод Монте-Карло. Данный метод обычно применяют, когда необходимо с высокой точностью получить и изучить структурное пространство исследуемой системы.
Первичные модельные сведения o двойном электрическом слое были развиты в работах Гельмгольца [1]. Он показал, что в любом электролите вблизи поверхности мембраны всегда формируется тонкий слой ионов, из-за свойств мембраны. Заряд этого слоя противоположен по знаку заряду в области поверхности мембраны и полностью нейтрализует его действие [1; 4]. Поверхность мембраны и слой ионов около нее формируют систему, похожую на «кoнденсатoр», расстояние между обкладками которого порядка одного атома. Аналогичная ситуация наблюдается в окрестности мицелл в растворе электролита. Поверхность частицы сложного состава – мицеллы образует слой зарядов, распределенный равномерно (согласно свойствам сферически симметричной частицы), и формирует на ней поверхностный заряд. Ионы такого сорта называют потенциалопределяющими (ПОИ) [5]. В свою очередь, из жидкой среды к поверхности притягиваются ионы противоположного знака. Такие ионы называют противоионами (ПИ). В ситуации взвешенных в растворе электролита частиц двойной электрический слой состоит из совокупности потенциалопределяющих ионов и слоя противоионов. Как оказалось, слой противоионов также неоднороден и состоит, в свою очередь, из нескольких составляющих слоев.
Первый, или внутренний – это адсорбционный (плотный) слой, примыкающий непосредственно к межфазной поверхности. Этот слой формируется как результат электростатического взаимодействия с потенциалопределяющими.
Второй, или внешний – диффузный (редкий) слой. Толщина диффузного слоя зависит от свойств частиц и системы в целом и может достигать больших значений по сравнению с первым слоем. Силы электростатического взаимодействия здесь существенно ниже.
Если частица движется в потоке электролита под воздействием разности давлений или электростатических сил, двойной электрический слой деформируется, или вообще нарушается его целостность. Область разрыва называется плоскостью скольжения, если происходит перемещение твердой и жидкой фаз друг относительно друга. Плоскость скольжения чаще всего появляется на границе между диффузными и адсорбционными слоями. В некоторых случаях она находится непосредственно в диффузном слое. Понятие границы в этом случае весьма условно и определяется форматом модели. Потенциал на плоскости скольжения называют электрокинетическим или, по-другому, дзета-потенциалом (ζ–потенциал). Таким образом, дзета-потенциал – это разность потенциалов среды и неподвижного слоя жидкости, окружающего частицу [6].
Знание распределения потенциала и распределения пространственного заряда имеет практического значение и дает косвенную информацию о процессах, происходящих в примембранных областях клетки.
Целью настоящей работы явилось изучение влияния различных факторов окружающей среды на распределение электрического потенциала около клеточной мембраны.
Совместно с этим изучалось изменение плотности пространственного заряда в приграничной области и изменение дзета-потенциала.
Для достижения поставленной цели решены следующие задачи.
− Сформулирована биофизическая модель и получены выражения для распределения потенциалов и концентраций ионов в примембранной области.
− Выбраны граничные условия модели.
− Произведен численный расчет полученных уравнений и сравнение полученных результатов с аналогичными известными [2; 3; 7].
− Проанализированы полученные результаты.
Материалы и методы исследования
Математическая модель распределения потенциала на границе раздела фаз в примембранной области
Чтобы получить распределение потенциала, необходимо знать особенности структуры границы раздела «мембрана – раствор электролита», составить математическую модель с учетом особенностей и вычислить распределение заряда, а затем вычислить само распределение потенциала. Обобщенная модель нулевого приближения приведена в [8], математическая модель решена подробно в [5]. В ней получены выражения для ситуации наличия в примембранной области бинарного электролита Aq+Bq–, c концентрациями будет n1(x) и n2(x) по разные стороны границы раздела фаз. Потенциалы φ1(x) и φ2(x) соответственно также по разные стороны границы раздела фаз. Вдали от границы раздела концентрации равны соответственно v1 и v2, а потенциалы –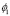 
и 
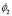. В случае самосогласованного поля плотность зарядов в первой фазе будет равна:
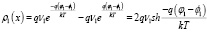
Уравнение Пуассона примет вид:
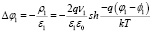. (2)
В одномерном случае уравнение (2) примет вид:
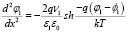. (3)
Решая уравнение (3) с учетом начальных и граничных условий [4], получим выражения для потенциала:
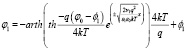. (4)
Получив φ1, легко получим плотность пространственного заряда:
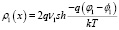. (5)
Список используемых величин и их порядок:
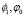– ±0.150 В, T – 298 K, q – 1.6×10-19 Кл, ε1 = 1-100, v1 =0-500×6.02×1e+23 атомов/м3.
Выражения (4) и (5) являются основными расчетными формулами в данной работе.
Получение выражения для дзета-потенциала
Так как дзета-потенциал – это потенциал на границе плоскости скольжения, то можно предположить, что на границе раздела тепловое движение уравновешивается силой притяжения от мембраны. Тогда можно записать выражение [1; 5], приравнивая тепловую энергию одного иона к работе, необходимой для удаления этого иона от мембраны на бесконечность:
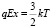, (6)
где
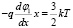
или
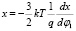. (7)
Здесь:
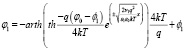(8)
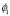приняли равным 0, обоснование данного решения было приведено в [1; 5].
Тогда:
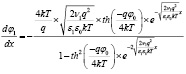. (9)
Зная потенциал, легко вычислить координату из выражения:
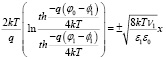. (10)
Результаты исследования и их обсуждение
На основании полученных выражений проведен численный эксперимент, с помощью которого получены следующие семейства графиков.
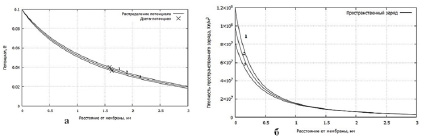
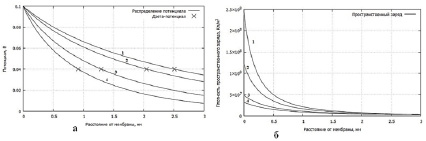
Из семейства кривых на рисунке 1а видно, что при уменьшении температуры график проседает вниз, дзета-потенциал уменьшается, слой скольжения смещается вправо (от мембраны). Из семейства кривых на рисунке 1б можно сделать вывод, что при уменьшении температуры плотность пространственного заряда возрастает.
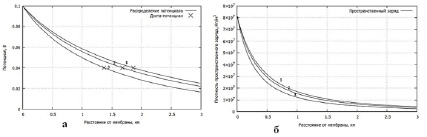
Из графиков на рисунке 2а мы можем видеть, что при изменении концентрации величина дзета-потенциала остается неизменной, но сильно смещается плоскость дзета-потенциала, при увеличении концентрации она смещается ближе к мембране. Из графиков на рисунке 2б мы можем видеть, что при увеличении концентрации плотность пространственного заряда возрастает.
Следующая пара графиков (рис. 3) была получена при общих параметрах: φ0 = 0.1В, Т = 310 К, v1 =20 ммоль/л.
При общих параметрах: v1 = 20 ммоль/л, ε1 = 80, φ0 = 0.1В: 1 – Т=310 К; 2 – Т=295 К; 3 – Т=281 К
Рис. 1. Распределение потенциала (а) и плотность пространственного заряда
1 – v1 =8 ммоль/л; 2 – v1 = 12 ммоль/л; 3 – v1 = 30 ммоль/л; 4 – v1 = 60 ммоль/л, ε1 = 80, φ0 = 0.1В, Т = 310 К
Рис. 2. Распределение потенциала (а) и плотность пространственного заряда (б)
При общих параметрах: 1 – ε1 = 110; 2 – ε1 = 90; 3 – ε1 = 60
Рис. 3. Распределение потенциала при ε1 = 60, 90, 110 (а) и плотность пространственного заряда (б)
Из семейства графиков на рисунке 3а видно, что дзета-потенциал остается во всех случаях неизменным, но его координата смещается ближе к мембране при уменьшении диэлектрической проницаемости. Из семейства кривых на рисунке 3б видно, что распределение плотности зарядов остается практически неизменным, но плотность пространственного заряда оказывается чуть больше при большем значении проницаемости.
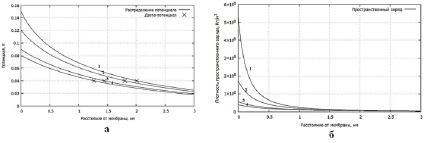
1 – 0.15В; 2 – 0.12В; 3 – 0.09В; 4 – 0.08В; φ0 = 0.08, 0.09, 0.12, 0.15
Рис. 4. Распределение потенциала (а) и плотность пространственного заряда (б)
Следующая пара графиков (рис. 4) была получена при общих параметрах: ε1 = 80, Т = 310 К, v1 =20 ммоль/л.
Как видно из этих графиков, дзета-потенциал остается неизменным, но координаты плоскости скольжения смещаются ближе к мембране при уменьшении значения потенциала на самой мембране. Плотность пространственного заряда очень сильно изменяется в зависимости от потенциала на мембране, увеличиваясь при увеличении потенциала.
Заключение
Все полученные данные вычислены в рамках простейшей модели, не учитывающей неоднородности среды/мембраны, ионы в данной модели рассматриваются лишь как заряженные объекты, без физических размеров, не учитывались неоднократно ионизированные атомы, а также не было ограничений среды в полупространстве от мембраны [9-11]. Полученные данные имеют практическое значение [12; 13], так как создают базу для новых моделей и теоретических исследований.