В настоящее время пристальное внимание уделяется экологическому мониторингу Байкальской природной территории (БПТ) [1]. Одной из насущных экологических проблем является использование малогабаритных котлов на угле на ИО данной территории [2]. Как правило, большая часть котлов характеризуется достаточно изношенным состоянием. В этой связи их оснащение дополнительным специальным оборудованием, в какой-то степени снижающим вредные выбросы, видится нецелесообразным. Поэтому исследование возможности полной или частичной замены таких котлов на экологически чистые источники тепла является актуальным.
От сжигания ископаемого топлива происходит много видов вредных выбросов [3–5]. Однако специалисты в области экологии уделяют особое внимание выбросам углекислого газа (CO2) [6]. Поэтому в статье рассматриваются только такие выбросы и используется методология их оценки, представленная в [7].
Таким образом, одной из практических целей моделирования последствий возможной замены источника тепла является оценка уменьшения выбросов CO2 от сжигания дизельного топлива или угля. Другим важным критерием являются затраты на теплонасосные установки, их установку и эксплуатацию. При этом существенную роль в процессе принятия решений по выбору модели теплового насоса играет оценка и сравнение вариантов значений вышеупомянутых критериев. Выбирается модель, для которой вариант значений критериев будет наилучшим в том или ином смысле. На практике специалистами в предметных областях востребованы, как правило, наиболее простые методы выбора, не требующие сбора и анализа большого объема дополнительной информации.
Целью исследования является формализация моделей дискретного многокритериального выбора на конечном множестве вариантов критериев (результатов имитационного моделирования процессов функционирования экологических установок ИО).
Материалы и методы исследования
Пусть имеется n критериев c1, c2, … , cn, отражающих характеристики функционирования экологической установки и ее эксплуатации. В качестве таких характеристик могут быть использованы расход энергии, обслуживаемая площадь ИО, надежность работы, сокращение объемов вредных выбросов, стоимость установки, затраты на его эксплуатацию, срок окупаемости и другие показатели. Для каждого критерия указана предпочтительность изменения его значений: cj → min или cj → max, j = 1,n. В соответствии с указанной предпочтительностью изменения значений критериев задаются ограничения на допустимые величины этих критериев: cj,min при cj → max, cj,max при cj → min.
Варианты значений критериев c1, c2, … , cn представлены матрицей A размерности m×n. Элемент матрицы ai,j содержит значение критерия cj в i-м варианте, i = 1,m, j = 1,n. Таким образом, i-я строка матрицы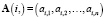 
соответствует i-му варианту значений критериев, а j-й столбец матрицы 
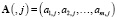представляет m вариантов значения j-го критерия.
Матрица B размерности m × n содержит оценки bi,j значений критериев ai,j, i = 1,m, j = 1,n. Данные оценки определяются путем упорядочения значений каждого критерия в разных вариантах по убыванию (возрастанию) при cj → min (cj → max) и назначения полученных индексов значений в частично-упорядоченном множестве в качестве оценок. Таким образом, наибольшая оценка соответствует наилучшему значению критерия.
Известен широкий спектр традиционных моделей дискретного многокритериального выбора [8, 9]. Зачастую их применение обуславливает необходимость использования информации о важности критериев, их рангах и весах, способах агрегирования и упорядочения, а также других дополнительных сведений [10].
В рамках данного исследования представленные в [11] правила многокритериального выбора, которые характеризуются минимальным объемом дополнительной информации, адаптированы к анализу результатов имитационного моделирования работы экологических установок. В их числе лексикографический и мажоритарный выбор, а также выбор по Парето.
Ниже приведены информационные структуры, описывающие дискретные модели выбора, базирующиеся на вышеупомянутых правилах многокритериального выбора.
Модель лексикографического выбора. Применение данного правила заключается в последовательном сравнении оценок значений критериев рассматриваемого варианта с оценками значений критериев остальных вариантов. Необходимая дополнительная информация состоит в том, что критерии c1, c2, … , cn упорядочиваются по степени их важности по убыванию.
Правило отбора i-го варианта:
,
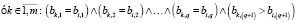ai,j ≥ cj,min при cj → max, ai,j ≤ cj,max при cj → min, i ∈ 1,m, j = 1,n, k ≠ i, q ∈ 1,n.
Модель мажоритарного выбора. В рамках данного правила выбор вариантов осуществляется по наибольшему числу критериев с наилучшими оценками их значений, содержащимися в варианте. Дополнительная информация не требуется.
Правило отбора i-го варианта:
,
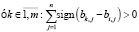ai,j ≥ cj,min при cj → max, ai,j ≤ cj,max при cj → min, i 1,m, j = 1,n, k ≠ i.
Модель выбора по Парето. В Парето-оптимальное множество отбираются варианты, для каждого из которых выполняется следующее условие: нет другого варианта, в котором оценки значений всех критериев больше или равны оценкам значений критериев рассматриваемого варианта, и при этом оценки значений хотя бы одного критерия в сравниваемых вариантах не равны. Дополнительная информация отсутствует.
Правило отбора i-го варианта:
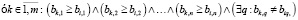
ai,j ≥ cj,min при cj → max, ai,j ≤ cj,max при cj → min, i ∈ 1,m, j = 1,n, k ≠ i, q ∈ 1,n.
Выбор единственного варианта. Если множество отобранных вариантов содержит r > 1 вариантов и необходимо единственное решение, то выполняется процедура сравнения отобранных вариантов с идеальным вариантом. Идеальный вариант e1, e2, … , en формируется из наилучших оценок для каждого критерия по всем вариантам:
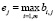, j = 1,n.
Сравнение реализуется с помощью декартовой метрики:
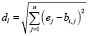, l = i1, i2, … , ir .
Единственное решение i* находится следующим образом:
.
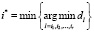Методика
Основными этапами методики применения дискретных моделей многокритериального выбора являются следующие:
1. Определение критериев c1, c2, … , cn.
2. Указание предпочтительности изменения значений критериев: cj → min или cj → max, j = 1,n.
3. Задание ограничений на допустимые величины критериев: cj,min при cj → max, cj,max при cj → min, j = 1,n.
4. Выбор используемой модели.
5. Если указана модель лексикографического выбора, то упорядочение критериев по важности.
6. Выполнение имитационного моделирования и формирование матрицы A значений критериев.
7. Нахождение матрицы B оценок значений критериев по матрице A.
8. Применение модели многокритериального выбора.
9. Если множество отобранных вариантов содержит более одного варианта и необходимо единственное решение, то выполнение процедуры сравнения отобранных вариантов с идеальным вариантом.
Пример
Проблема моделирования работы экологических установок (тепловых насосов) на ИО БПР и подход к процессу ее решения рассмотрены в [12]. Общие результаты расчетов, полученные в процессе изучения работы теплонасосных установок при частичном замещении ими малогабаритных котлов на угле, приведены в [13].
В данном разделе представлены оценки уточненных значений двух критериев c1 (размер капитальных вложений) и c2 (сокращение объемов выбросов CO2) для двенадцати вариантов различных сочетаний моделей тепловых насосов и режимов их эксплуатации, а также результаты применения разработанных моделей дискретного многокритериального выбора по этим оценкам. В частности, в табл. 1 приведены результаты лексикографического выбора при двух способах упорядочения критериев по важности:
1) c1 и c2 (столбцы 4–7 табл. 1) представляют соответственно размер капитальных вложений и сокращение объемов выбросов CO2;
2) c1 и c2 (столбцы 8–11 табл. 1), наоборот, отражают сокращение объемов выбросов CO2 и размер капитальных вложений.
В первом случае сравнение вариантов начинается с первого критерия, оценка значения которого в двенадцатом варианте, выделенная зеленым цветом заливки ячейки таблицы, однозначно является лучшей. Во втором случае главным критерием при сравнении вариантов является второй критерий. Наилучшие оценки его значений, выделенные желтым цветом, содержатся во втором и восьмом вариантах. Поэтому для этих вариантов производится дополнительное сравнение по первому критерию, которое показывает преимущество оценки значения данного критерия в восьмом варианте. Найденная оценка выделена зеленым цветом.
Таблица 1
Результаты применения модели лексикографического выбора
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
i |
Модель |
Режим |
ai,1, тыс. руб. |
ai,2, т |
bi,1 |
bi,2 |
ai,1, т |
ai,2, тыс. руб. |
bi,1 |
bi,2 |
|
1 |
1 |
1 |
1670,01 |
130,96 |
1 |
5 |
130,96 |
1670,01 |
5 |
1 |
|
2 |
2 |
1 |
1661,30 |
132,59 |
2 |
6 |
132,59 |
1661,30 |
6 |
2 |
|
3 |
3 |
1 |
1600,30 |
129,90 |
3 |
4 |
129,90 |
1600,30 |
4 |
3 |
|
4 |
5 |
1 |
1565,45 |
103,29 |
4 |
2 |
103,29 |
1565,45 |
2 |
4 |
|
4 |
5 |
1 |
1539,31 |
105,77 |
5 |
3 |
105,77 |
1539,31 |
3 |
5 |
|
6 |
6 |
1 |
1504,45 |
102,68 |
6 |
1 |
102,68 |
1504,45 |
1 |
6 |
|
7 |
1 |
2 |
1417,44 |
130,96 |
7 |
5 |
130,96 |
1417,44 |
5 |
7 |
|
8 |
2 |
2 |
1408,73 |
132,59 |
8 |
6 |
132,59 |
1408,73 |
6 |
8 |
|
9 |
3 |
2 |
1347,73 |
129,90 |
9 |
4 |
129,90 |
1347,73 |
4 |
9 |
|
10 |
4 |
2 |
1312,88 |
103,29 |
10 |
2 |
103,29 |
1312,88 |
2 |
10 |
|
11 |
5 |
2 |
1286,74 |
105,77 |
11 |
3 |
105,77 |
1286,74 |
3 |
11 |
|
12 |
6 |
2 |
1251,88 |
102,68 |
12 |
1 |
102,68 |
1251,88 |
1 |
12 |
Таблица 2
Результаты применения моделей мажоритарного выбора и выбора по Парето
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
i |
Модель |
Режим |
ai,1, т |
ai,2, тыс. руб. |
bi,1 |
bi,2 |
d1, l = 2,8,12 |
ai,1, т |
ai,2, тыс. руб. |
bi,1 |
bi,2 |
dl, l = 8,9,11.12 |
|
1 |
1 |
1 |
130,96 |
1670,01 |
5 |
1 |
– |
130,96 |
1670,01 |
5 |
1 |
– |
|
2 |
2 |
1 |
132,59 |
1661,30 |
6 |
2 |
10,00 |
132,59 |
1661,30 |
6 |
2 |
– |
|
3 |
3 |
1 |
129,90 |
1600,30 |
4 |
3 |
– |
129,90 |
1600,30 |
4 |
3 |
– |
|
4 |
5 |
1 |
103,29 |
1565,45 |
2 |
4 |
– |
103,29 |
1565,45 |
2 |
4 |
– |
|
4 |
5 |
1 |
105,77 |
1539,31 |
3 |
5 |
– |
105,77 |
1539,31 |
3 |
5 |
– |
|
6 |
6 |
1 |
102,68 |
1504,45 |
1 |
6 |
– |
102,68 |
1504,45 |
1 |
6 |
– |
|
7 |
1 |
2 |
130,96 |
1417,44 |
5 |
7 |
– |
130,96 |
1417,44 |
5 |
7 |
– |
|
8 |
2 |
2 |
132,59 |
1408,73 |
6 |
8 |
4,00 |
132,59 |
1408,73 |
6 |
8 |
4.00 |
|
9 |
3 |
2 |
129,90 |
1347,73 |
4 |
9 |
– |
129,90 |
1347,73 |
4 |
9 |
3.61 |
|
10 |
4 |
2 |
103,29 |
1312,88 |
2 |
10 |
– |
103,29 |
1312,88 |
2 |
10 |
– |
|
11 |
5 |
2 |
105,77 |
1286,74 |
3 |
11 |
– |
105,77 |
1286,74 |
3 |
11 |
3.16 |
|
12 |
6 |
2 |
102,68 |
1251,88 |
1 |
12 |
5,00 |
102,68 |
1251,88 |
1 |
12 |
5.00 |
В табл. 2 показаны результаты применения моделей мажоритарного выбора (столбцы 4–8) и выбора по Парето (столбцы 9–13). Здесь c1 и c2 представляют сокращение объемов выбросов CO2 и размер капитальных вложений. В случае мажоритарного выбора множество отобранных вариантов включает второй, восьмой и двенадцатый варианты. Наилучшие оценки критериев c1 и c2, содержащиеся в этих вариантах, выделены желтым цветом. Так как во всех трех вариантах содержится ровно по одной наилучшей оценке значений критериев, требуется проведение дополнительной процедуры сравнения с идеальным вариантом (e1 = 12, e2 = 6). Расстояния трех сравниваемых вариантов до идеального представлены в восьмом столбце табл. 2. Наилучшее расстояние выделено зеленым цветом. Оно соответствует восьмому варианту.
В случае выбора по Парето при первичном сравнении отобраны восьмой, девятый, одиннадцатый и двенадцатый варианты. Содержащиеся в них оценки значений критериев показаны желтым цветом. По результатам дополнительного сравнения выбранных вариантов с идеальным одиннадцатый вариант является наилучшим. Соответствующее расстояние (столбец 13 в табл. 2) выделено зеленым цветом.
Таким образом, приведенный выше простой иллюстративный пример показывает достаточную гибкость в применении разработанных дискретных моделей многокритериального выбора в зависимости от целей исследования, значимости критериев и наличия дополнительной информации.
Заключение
Предложены новые модели многокритериального выбора по результатам имитационного моделирования. Применение моделей продемонстрировано на примере выбора тепловых насосов для ИО БПТ с учетом сокращения выбросов CO2 и финансовых затрат на размещение и эксплуатацию системы отопления с помощью теплового насоса. Возможно развитие и использование разработанных моделей в других предметных областях. Примеры употребления таких адаптированных моделей в процессе решения ряда задач, связанных с исследованием систем энергетики, приведены соответственно в [14, 15].
Исследование проведено при поддержке РФФИ и Правительства Иркутской области, проект № 20-47-380002-р_а «Математическое и информационное моделирование инфраструктурных объектов Байкальской природной территории», а также Министерства науки и высшего образования Российской Федерации, проект № FWEW-2021-0005 «Технологии разработки и анализа предметно-ориентированных интеллектуальных систем группового управления в недетерминированных распределенных средах».