Несмотря на большие успехи, достигнутые в последние годы в области математического моделирования в гидродинамике, проблема описания генерации и нелинейного распространения волн в жидкости и газе по-прежнему остается актуальной. Для нелинейных процессов, где дисперсией можно пренебречь, основным аппаратом исследования служит теория гиперболических дифференциальных уравнений, описывающая распространение волн в однородной жидкости со свободной поверхностью. Центральным эффектом в гиперболических системах являются возникновение ударных волн (скачков) и потеря регулярности движения. При этом можно получить многие классы точных решений, описывающие важные классы движений жидкости со свободной поверхностью, и исследовать групповые свойства рассмотренных уравнений [1-3]. Как правило, в геофизических приложениях анализируются модели, не учитывающие вертикальную структуру воды, т.е. задачи, усредненные по некоторому (в нашем случае – по плоскому) слою жидкости [4]. Тонкая структура процесса, связанная с взаимодействием вертикального и горизонтального движений, либо учитывается очень грубо, либо не учитывается вообще (речь идет о сильно нелинейных процессах). На этом фоне несколько особняком стоит весьма общая модель для длинных волн на воде с ровным дном и свободной поверхностью, которая впервые была рассмотрена Бенни [5]. Особенность этой задачи состоит в том, что здесь происходит самосогласованное взаимодействие между основным горизонтальным и вертикальным движением. В работе [6] на основе бесконечной системы законов сохранения для уравнений Бенни было предложено новое кинетическое интегро-дифференциальное уравнение, где свободная поверхность является лишь одним из моментов функции распределения, которая соответствует данной системе моментов. Полученное уравнение описывает взаимодействие нелинейности и завихренного слоя жидкости для бесконечно длинных волн. Предложенное в настоящей работе исследование позволяет вывести новое кинетическое уравнение, описывающее динамику длинных волн конечной длины; полученные результаты являются обобщением и развитием результатов работы [6]. Таким образом, в настоящей работе рассматривается разложение произвольной дисперсии около нулевого волнового числа. Групповой анализ уравнений безвихревого предела и изучение динамики линеаризованных уравнений позволили выяснить корректность и универсальность рассмотренной модели. В частности, это дало возможность понять и описать в гидродинамике волн со свободной поверхность такой эффект, как затухание Ландау, ранее известный для электростатических волн в электронной плазме.
Цель настоящей работы – получение и анализ новых уравнений, описывающих распространение длинных сильно нелинейных волн, распространяющихся в тяжелой однородной жидкости со свободной поверхностью.
Материал и методы исследования
В настоящей работе при рассмотрении длинных волн на воде в гидростатическом приближении на завихренной жидкости (сильно нелинейные волны) рассматривается модель Бенни [5]:
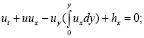
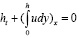. (1)
Здесь t – время, x – продольная пространственная координата, y – вертикальная пространственная координата, h(t, x) – неизвестная высота свободной поверхности однородной тяжелой жидкости, (g ≠ 0), u(t, x, y) – горизонтальная компонента скорости жидкости. Индекс внизу означает производную по соответствующей переменной. В рассматриваемой системе координат ускорение свободного падения g = 1, плотность жидкости также равна 1, зависимые и независимые переменные задачи обезразмерены.
Задачи с неизвестной свободной границей трудно решать, поэтому весьма важной представляется проблема сведения системы (1) к уравнениям, которые не содержат в себе неизвестной свободной поверхности, в данном случае – к некоторым интегро-дифференциальным уравнениям, аналогичным тем, что возникают в теории бесстолкновительной плазмы.
Кинетическое уравнение для описания длинноволновых движений в завихренной жидкости
Введем бесконечную систему моментов
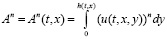. (2)
Бенни было показано, что система уравнений (1) порождает следующую бесконечную систему уравнений для моментов [5]:
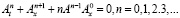(3)
В работе [6] было предложено кинетическое уравнение власовского типа, эквивалентное бесконечной цепочке связанных уравнений (3). Введем функцию распределения (плотность вероятности) f(t, x, v), которую далее пока будем записывать как f(v), рассматривая переменные t, x как параметры. Для f(v) определим характеристическую функцию следующим образом:
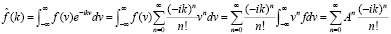. (4)
Здесь
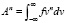. (5)
Тогда корректно следующее выражение функции f(v) через моменты функции f:
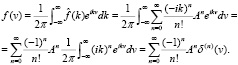(6)
Здесь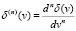 
– это производная функционала Дирака соответствующего порядка. Таким образом, по данным моментам функция распределения f(v) восстанавливается однозначно как обобщенная функция, действующая, например, на функции из пространства Шварца по переменной v. Такие функции обладают моментами 
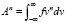для любого целого числа n ≥ 0.
Справедлива следующая теорема (см. [6]).
Теорема. Если функция распределения определена с помощью формулы
,
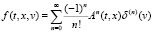где моменты An(t, x) удовлетворяют бесконечной моментной системе уравнений (3), то функция распределения является регулярной обобщенной функцией и удовлетворяет интегро-дифференциальному уравнению
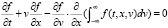. (7)
Описание классической теории мелкой воды и ее вихревых обобщений
Пусть горизонтальная компонента скорости жидкости u(t, x) не зависит от переменной y. Тогда характеристическая функция и функция распределения принимают следующий вид:
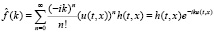, (8)
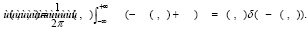(9)
При этом функции h(t, x), u(t, x) удовлетворяют классической системе уравнений мелкой воды:
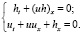
Рассмотрим теперь обобщение кинетического уравнения (7), а именно:
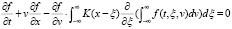(10)
Здесь K(x) – это либо обычная, либо обобщенная функция переменной x.
Рассмотрим конкретный вид функции распределения, соответствующий холодному газу (мелкой воде), а именно: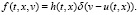 
Тогда кинетическое уравнение сведется к следующей обобщенной системе уравнений мелкой воды:
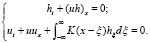(11)
Если произвести линеаризацию системы (11) относительно однородного состояния, u = u0 + εu1, h = h0 + εh1, то получим следующую систему уравнений:
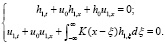(12)
Переходя в движущуюся систему координат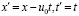 
и обозначая новые координаты без штрихов, получаем такую систему уравнений:
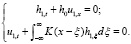(13)
Чтобы вычислить дисперсию в рассмотренной системе, рассмотрим частные решения системы (13) следующего вида:
,
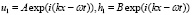такие, что A ≠ 0, B ≠ 0. После стандартных преобразований получим дисперсионное соотношение:
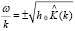. (14)
Следовательно, если функция K(x) произвольна, то это означает, что мы рассматриваем модель с произвольной дисперсией, с произвольной фазовой скоростью ω / k. Мы рассматриваем динамику, учитывающую следующее приближение по длине волны для уравнений мелкой воды. Так как для уравнения Бенни K(x) = δ(x), где δ(x) – обобщенная функция Дирака, то K(x) в общем случае имеет следующий вид:
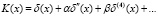. (15)
Четные производные от функции Дирака возникают из требования вещественности дисперсионного соотношения. После преобразования Фурье соотношение (15) примет следующий вид:
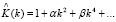. (16)
Именно соотношение (16) и будет рассматриваться в дальнейшем, как правило, при малых 
.
Результаты исследования и их обсуждение
Групповые свойства и некоторые точные решения для теории мелкой воды с дисперсией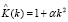 
Рассмотрим систему уравнений мелкой воды при учете дисперсии в первом приближении:
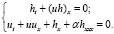(17)
Проверкой естественности моделирования движений длинных волн служит изучение групповых свойств системы (17) с использованием техники группового анализа [7, 8]. Можно доказать, что множество всех точечных преобразований (преобразований Ли) для системы (17) порождается следующими дифференциальными операторами:
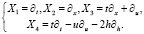
Первые три оператора представляют собой генераторы одномерной группы преобразований Галилея, оператор X4 порождает группу масштабных преобразований. Группа Галилея допускается для всех значений α, а оператор X4 – для всех α ≠ 0. Отметим, что при этом вид оператора X4 не зависит от количественного значения α ≠ 0, что говорит об универсальности выбранного разложения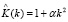 
.
Классические уравнения мелкой воды как над ровным дном, так и неровным хорошо исследованы с групповой точки зрения [1]. Методы решения таких уравнений тесно связаны с тем фактом, что все производные в задаче – первого порядка и, в частности, здесь применим метод годографа. Кроме того, решены некоторые задачи (получены точные решения), имеющие непосредственное прикладное значение [2-4].
Приведем пример точного, инвариантного относительно оператора X4 решения, которое нетривиально зависит от параметра дисперсии α ≠ 0:
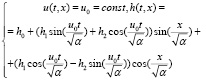( 18)
Здесь u0, h0, h1, h2, – произвольные постоянные.
С целью качественного анализа приведенного выше решения h(t, x) зафиксируем постоянные u0, h0, h1, h2; возьмем, например, u0 = 6; α = 0,5; h0 = 1; h1 = 1; h2 = –2; Рассмотрим полученную функцию h(t, x) при нескольких значениях t; например, возьмем t = 0, t = 10, t = 20.
На рисунке 1 приведены графики зависимости функции h(x) = h(t, x) (высоты свободной поверхности жидкости) от переменной x при вышеуказанных значениях времени t и параметров u0, h0, h1, h2. Отметим, что при t = 0 и t = 20 графики оказались совпадающими (кривая зеленого цвета); кривая желтого цвета соответствует случаю t = 10.
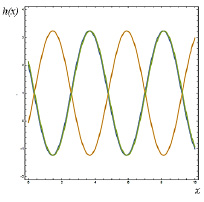
Рис. 1. Графики решения h(x) = h(x,t), определяемого формулой (18), при различных значениях времени t и фиксированных значениях параметров u0, h0, h1, h2
Анализ этих графиков показывает, что наличие дисперсии (α ≠ 0) порождает колебательные движения высоты свободной поверхности жидкости. Осциллирующие решения в задаче с третьей пространственной производной характерны, например, для уравнения Кортевега-де-Фриза [9]. Таким образом, в данном случае (в отличие от случая классической теории мелкой воды) не все решения рассматриваемой нелинейной системы становятся многозначными, а соответствующие им волны «опрокидываются».
В дальнейшем дисперсию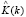 
можно называть продольной дисперсией, так как она присутствует и в случае холодного газа (плазмы), и в нашем случае при отсутствии вертикального перемешивания жидкости.
Затухание Ландау для длинных волн на воде в жидкости со свободной поверхностью для произвольной дисперсии
Запишем теперь основное уравнение (10) в виде системы уравнений, так, чтобы проявилось формальное сходство с одномерными уравнениями Власова в плазме:
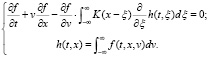(19)
Линеаризуем систему (19) относительно функции распределения f0(v). Это означает, что мы рассматриваем сдвиговое течение:
u = u0(y), h(t, x) = H = const.
Задавая сдвиговое течение в виде бесконечного числа моментов
,
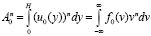можно представить в явном виде функцию
.
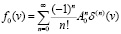Мы считаем f0(v) регулярной обобщенной функцией, так что обычная функция f0(v) является аналитической функцией переменной v. Все конкретные примеры будут удовлетворять этому условию.
Представляем решение в таком виде:
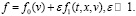
Тогда линеаризованное уравнение примет следующий вид:
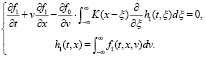(20)
Преобразования Лапласа L и Фурье F возьмем в такой форме:
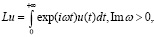
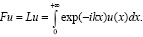(21)
Применяя преобразования (21) к системе (20), получим, что:
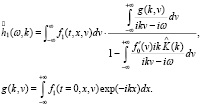(22)
Уравнение
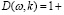
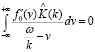(23)
называется дисперсионным соотношением системы (21). Можно назвать его обобщенным дисперсионным соотношением Ландау. Можно доказать, что уравнение (23) имеет конечное число нулей при любых фиксированных вещественных k, Imω > 0. Смысл Imω > 0 состоит в том, что если вместо строго гармонического (ω – вещественно) решения рассмотрим процесс, который включается при t = –∞, так что f1 = 0, h1 = 0 при t = –∞, тогда необходимо условие Imω > 0. Решение при этих условиях описывает незатухающие колебания жидкости и растет при t → +∞. Функция D(ω,k) при каждом фиксированном значении переменной k аналитична по переменной ω в полуплоскости Imω > 0 [9].
Фиксируем вещественное число k ≠ 0. Затухающая гармоническая волна при t → +∞ существует только тогда, когда Imω < 0. Следовательно, D(ω,k) должно аналитически продолжаться в часть полуплоскости Imω < 0. Чтобы такое аналитическое продолжение существовало (так как (23) представляет собой интеграл типа Коши), необходимо требование аналитичности функции f0(v) по переменной v [10]. В частности, если f0(v) – целая функция, то D(ω,k) продолжается на комплексную переменную как целая функция переменной ω.
Пусть
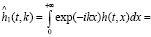
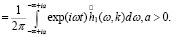
Приведем далее некоторые достаточные математические условия, при которых возникает затухание Ландау [10].
1. Пусть область G – полоса |Imω| ≤ a, a < 0. Тогда функция f0(v) аналитична в полосе G и при этом выполнены следующие условия: при |b| ≤ a
,
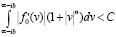постоянная C не зависит от b, n – натуральное произвольное число.
2. Для всякого n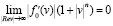 
.
3. Пусть g(k, v) аналитична в полосе G, за исключением конечного числа полюсов ω1, … ωm, не лежащих на границе области G. Тогда:
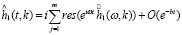. (24)
Таким образом, затухание Ландау возникает, если все полюса лежат в полуплоскости Imω < 0. При больших временах асимптотика решения определяется наиболее высоко лежащим полюсом.
Приближенное вычисление коэффициента затухания Ландау вблизи длинноволнового предела (k ≠ 0).
Считая на этом этапе число ω = ωr вещественным, вычислим
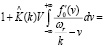(25)
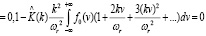
где интеграл понимается в смысле главного значения по Коши при очень малых k ≠ 0.
Выберем систему координат так, что:
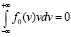. (26)
Тогда получим следующее выражение для групповой скорости в случае произвольной продольной дисперсии и малой вихревой дисперсии до порядка k2:
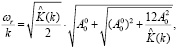(27)
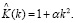(28)
Это означает, что мы рассматриваем произвольную дисперсию в окрестности бесконечно длинных волн. Заметим, что универсальность представления (28) обсуждалась также и выше.
На рисунке 2 приведены графики зависимости фазовой скорости ωr / k от волнового числа k при разных значениях параметра α рассматриваемой модели и при фиксированных значениях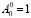 
и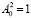 
(см. (27)); кривые синего, желтого и зеленого цвета соответствуют значениям α = 0,01, α = 0,1, α = 1. Фазовая скорость показывает скорость распространения фазы волны (например, возвышений волн).
Зависимость фазовой скорости от параметра α позволяет связать теоретическую модель с экспериментальными данными.
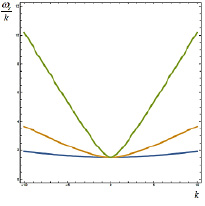
Рис. 2. Графики фазовой скорости ωr / k, определяемой формулой (27), при различных значениях α; кривые синего, желтого и зеленого цвета соответствуют α = 0,01, α = 0,1 и α =1
Собирая члены порядка k2, получаем следующую формулу:
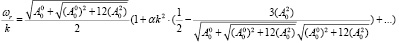(29)
Продолжим дисперсионное соотношение (23) в комплексную плоскость; из того, что f0(v) – аналитическая функция, следует, что это можно сделать в область Imω < 0. Пусть теперь Imω → 0_, т.е. контур обходит полюса снизу. Тогда в пределе мы получим, используя формулы Сохоцкого–Племеля, что:
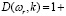
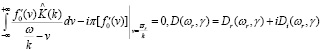(30)
Продолжим теперь уже формулу (30) в комплексную область и, отбрасывая малые высокого порядка при ω = ωr + iγ, найдем:
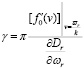. (31)
Отсюда находим, оставляя величины порядка k2, что:
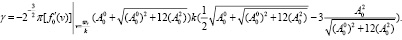(32)
Здесь:
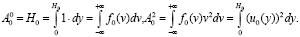
Возможно, что самый важный результат этого исследования состоит в том, что коэффициент затухания или усиления гармонической волны не зависит от коэффициента продольной дисперсии α. Существенно только условие α ≠ 0.
Приведем окончательный результат для случая максвелловской функции распределения
, 
.
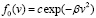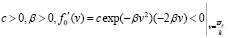Выразим константы c и β через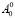 
и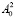 
. Имеем:
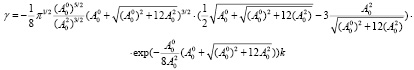
Очевидно, что γ < 0 при выполнении неравенства
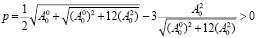, (33)
и мы будем иметь затухающую волну с коэффициентом затухания exp(γt), γ < 0. Здесь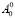 
– это масса слоя жидкости единичной поперечной ширины, 
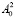– кинетическая энергия продольного движения слоя жидкости единичной поперечной ширины. Назовем функцию p , зависящую от 
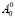и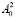 
, фактором устойчивости. Таким образом, результат развития возмущения в жидкости не зависит от тонкой структуры завихренности внутри слоя жидкости. Принципиально важна только конечность длины волны, k ≠ 0.
На рисунке 3 на плоскости с координатам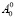и 
и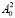 
приведен график кривой p = 0. Эта кривая разделяет плоскость параметров на две области – устойчивости (затухания возмущений) и неустойчивости (нарастания возмущений). Для определения того, какая же из этих областей соответствует устойчивости, можно построить аналогичную кривую при каком-либо значении p > 0. На рисунке 3 в качестве примера приведены кривые для p = 1, p = 2, позволяющие выделить зону устойчивости (она расположена ниже кривой p = 0). В зоне устойчивости длинные волны затухают.
Анализ приведенных графиков позволяет понять общие принципы строительства береговых защитных сооружений на море: эти сооружения должны сокращать длину береговой линии, доступную для воздействия волн.
Для визуализации полученных результатов был использован пакет программ «WOLFRAM MATEMATICA».
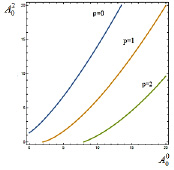
Рис. 3 Линии уровня функции p = p(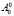
, 
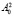), разделяющие зоны устойчивости и неустойчивости (p = 0), а также указывающие зону устойчивости (p = 1, p = 2)
Заключение
В работе построены новые уравнения, описывающие распространение длинных волн в тяжелой жидкости со свободной поверхностью. Важным результатом является совмещение действия вихревой динамики жидкости и дисперсии безвихревого предела уравнений движения жидкости со свободной поверхностью. В качестве основы анализа осуществлен переход от гидродинамических уравнений бесконечной цепочки законов сохранения, которую удается описать с помощью интегро-дифференциального уравнения с самосогласованным полем. Результаты анализа интегро-дифференциального уравнения (в частности, временная асимптотика линеаризованного уравнения) носят универсальный характер и выражаются только двумя числами, определяемыми по исходной функции сдвиговой скорости, и не зависят от параметра разложения продольной дисперсии α. Вместе с независимостью алгебры симметрии безвихревой мелкой воды от α это говорит об универсальности рассмотренной модели.
Длинные волны любой конечной длины затухают при дополнительном условии (33). Выполнение или невыполнение условия (33) определяет действие завихренности на гармонические волны, при этом возможно как их усиление, так и затухание.
Отметим, что описание вихревой динамики вызывает значительные затруднения как в гидродинамике несжимаемой жидкости, так и для сжимаемых сред и, как правило, требует численного анализа [11]. Однако предлагаемый в настоящей работе асимптотический подход позволяет сразу получить необходимые условия затухания волн при неизвестных значениях параметра задачи α.
Полученные результаты могут быть применены в области геофизической гидродинамики, так как предлагаемую математическую модель можно обобщить и на случай длинных волн в жидкости с переменной глубиной, т.е. волн с характеристиками «почти цунами» (очень длинных волн). В частности, расчет силового воздействия длинных волн на береговые сооружения можно производить, используя не только классическую теорию мелкой воды, но и полученные в настоящей работе уравнения, так как вблизи береговой зоны вода сильно завихрена. При этом волнозащитные сооружения (защищающие прибрежную инфраструктуру) можно проектировать, подбирая значение фактора устойчивости так, чтобы попасть в режим затухания очень длинных волн.