Пандемия COVID-19 и массовый переход системы образования на дистанционный формат выявили серьезные проблемы в оценке результатов обучения во многих национальных образовательных системах, в том числе в российской. Как оказалось, при большом разнообразии платформ для онлайн-обучения отсутствует надежный инструментарий для дистанционной, массовой и объективной оценки уровня сформированности компетенций, что привело к переносу и даже отмене итоговых аттестаций.
Проблема оценки уровня сформированности компетенций, возникшая с переходом образования на компетентностную модель, является ключевой и до конца не решенной для современного российского образования. Задача оценки достижений обучающихся в некоторой дисциплине, возникающая на всех этапах обучения, еще более усложняется, так как каждая дисциплина, как правило, формирует от двух до четырех и более компетенций. Поэтому задача ставится таким образом, что в ходе промежуточной аттестации во время одной процедуры оценивания необходимо определить уровень сформированности всех этих компетенций. Схожие задачи возникают перед экспертом во время процедуры аккредитации образовательных программ, когда за один сеанс мультидисциплинарного тестирования на основе ответов на 20–30 контрольных вопросов необходимо оценить уровень сформированности 4–5 компетенций. Решить подобную многомерную задачу оценки компетенций, используя простые линейные алгоритмы анализа результатов тестирования, невозможно.
С другой стороны, использование сложных методов анализа результатов тестирования с элементами искусственного интеллекта [1] порождает другую проблему, обусловленную недостаточным уровнем доверия к подобным системам оценки, как со стороны обучающихся, так и со стороны преподавателей. Уровень доверия к интеллектуальным системам сильно зависит от степени прозрачности такой системы, простоты и понятности используемых в ней алгоритмов. Например, если мы будем использовать для оценки нейронную сеть, то вряд ли удастся убедить пользователей этой системы оценивания в достоверности выдаваемых результатов, как бы хорошо мы ни проектировали и обучали ее, так как для пользователей она будет черным ящиком. Проблема доверия к системам оценки обострилась именно в период пандемии, вместе с повсеместным использованием дистанционных образовательных технологий. Другим недостатком существующих систем тестирования и анализа результатов является часто критикуемый формальный механистический подход, не учитывающий индивидуальные особенности обучаемого [2]. Поэтому часто звучат призывы вернуться к старой «советской» системе оценивания.
Целью является разработка адаптивной методики оценивания уровня сформированности нескольких компетенций, исходя из результатов одного сеанса тестирования, позволяющей в режиме реального времени подстраиваться под индивидуальные особенности обучаемого.
Для решения поставленной задачи существующие методы обработки результатов тестирования не подходят. Традиционная линейная модель, основанная на дихотомической или политомической шкале измерения ответов, позволяет оценить уровень знаний обучаемого. Однако по полученным с ее помощью результатам нельзя достоверно определить уровень компетентности. Пришедшая ей на смену классическая IRT-модель также не позволяет решить поставленную задачу по нескольким причинам.
Во-первых, классическая модель Раша требует, чтобы вопросы теста относились к одной области знаний, только в этом случае с ее помощью можно корректно оценить уровень подготовленности тестируемых [3]. Во-вторых, при проведении промежуточного или итогового контроля по дисциплине не всегда имеется достаточное количество результатов тестирования для того, чтобы провести калибровку теста [4]. Тем не менее эта модель хорошо зарекомендовала себя и прошла серьезную апробацию при оценке результатов ЕГЭ, а также в международных исследованиях (PISA, TIMMS).
Предлагается адаптировать IRT для решения следующей задачи. Требуется определить уровень сформированности нескольких компетенций в ходе одного сеанса тестирования. При этом желательно использовать имеющиеся банки тестовых заданий, трудность каждого задания в которых оценена с точки зрения каждой компетенции.
Материалы и методы исследования
В основу имитационной модели, построенной в данной работе, положена следующая идея. Предполагается, что для правильного выполнения задания требуется определенный уровень развития нескольких компетенций. Проблема заключается в оценке влияния каждой компетенции на вероятность правильного ответа. Как известно, в классической модели Раша эта вероятность описывается логистической кривой и зависит от разности между трудностью задания и уровнем подготовленности испытуемого.
В случае нескольких компетенций появляется неопределенность, что понимать под уровнем подготовленности и как он соотносится с уровнем сформированности каждой компетенции. Некоторые авторы предлагают определять уровень подготовленности как линейную комбинацию уровней сформированности компетенций с соответствующими весовыми коэффициентами [5, 6].
Считается, что каждое задание обладает различными чувствительностями ai по отношению к различным компетенциям. Испытуемый также обладает различными уровнями освоения компетенций θn (n – номер компетенции). Результирующая компетенция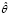 
для данного задания оценивается как линейная комбинация компетенций:
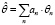. (1)
Однопараметрическая модель Раша в этом случае выглядит так
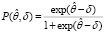, (2)
где δ – трудность задания.
Однако при таком методе расчёта остается открытым вопрос, как установить значение весовых коэффициентов и вклад каждой компетенции в вероятность правильного ответа на данное задание. Мы предлагаем другой подход к оценке вероятностей и уровней сформированности каждой компетенции.
Для иллюстрации предлагаемого подхода рассмотрим следующий модельный пример. Пусть испытуемому поставлено задание: переправиться через широкую реку. Для выполнения задания он может переплыть реку, проявив искусство пловца, построить плот, проявив мастерство в его постройке, или договориться с лодочником, проявив искусство переговорщика. То есть для выполнения задания требуются три компетенции, хотя и в разной степени. Однако если испытуемый решил построить плот, то неважно, как хорошо он умеет плавать или договариваться. Этой ситуации, когда для решения поставленной задачи испытуемый использует наиболее развитую, с его точки зрения, компетенцию, соответствует представленная в работе имитационная модель, на которой будут сравниваться различные алгоритмы и методики тестирования.
Для определенности предполагается, что одновременно измеряются значения трех компетенций и задания имеют разные уровни трудности для каждой из них. Обозначим уровни трудности задания по отношению к каждой компетенции δ1, δ2 и δ3, а уровни их сформированности у студента θ1, θ2 и θ3 соответственно.
В данном случае в соответствии с моделью Раша получаем три разные вероятности правильного ответа:
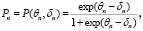(3)
где n = 1, 2, 3 – порядковый номер компетенции.
В качестве вероятности выполнения тестового задания в предлагаемой модели выбирается максимальное значение из этих трех вероятностей в соответствии с предположениями, положенными в основу имитационной модели: во-первых, при выполнении задания испытуемый, стараясь показать наилучший результат, применяет именно ту компетенцию, которая позволяет выполнить его с наибольшей вероятностью; во-вторых, каждая компетенция проявляется независимо от других и может быть оценена с помощью модели Раша.
Следующее предположение состоит в том, что уровень сформированности каждой компетенции оценивается по четырехбалльной шкале, что соответствует сложившейся практике оценивания при проведении промежуточных и итоговых аттестаций.
Установим следующее соответствие между используемой шкалой оценивания и уровнем развития компетенций в логитах: отлично – 3, хорошо – 1, удовлетворительно – минус 1 и неудовлетворительно – минус 3. В случае одновременного оценивания трех компетенций возможны 64 уникальные комбинации уровней их сформированности по такой четырехбалльной шкале, что будет соответствовать 64 типам (паттернам) студентов. Предполагается, что удалось сформировать банк тестовых заданий, уровни трудности которых относительно каждой компетенции меняются с тем же шагом по шкале трудностей. Таким образом, банк вопросов содержит 64 типа заданий с уникальными комбинациями трудностей по всем компетенциям. Задача оценивания компетенций студента в таком случае сводится к задаче определения паттерна, к которому студент относится, т.е. к задаче классификации [7].
Введем обозначения: P(k)(Hj) – вероятность принадлежности испытуемого к j-му паттерну, вычисленная на k-м шаге, т.е. когда получены ответы на k вопросов; PA(j,m), PnotA(j,m) – вероятности того, что студент, принадлежащий j-му паттерну, правильно выполнит задание, относящееся к типу m (m = 1...64), или не справится с этим заданием соответственно; k – номер шага (количество полученных ответов) [8].
Перед первым заданием предполагается, что вероятности принадлежности к каждому паттерну распределены равномерно и равны P(0)(Hj)=1/64, j=1…64. После выполнения очередного задания, относящегося к типу m, вероятности принадлежности к каждому паттерну пересчитываются по формуле Байеса (суммирование в знаменателе дроби проходит по всем паттернам) и выбирается паттерн, вероятность принадлежности к которому максимальна [9]:
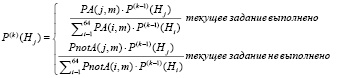(4)
Результаты исследования и их обсуждение
В имитационной модели испытаниям подвергался студент с заданным уровнем развития компетенций. Результат его ответа на каждый вопрос определялся как максимум из вероятностей, рассчитанных по формуле (3).
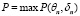, (5)
где n = 1, 2, 3 – порядковый номер компетенции
Вероятности принадлежности данного студента к каждому паттерну пересчитывались после получения ответа на очередной вопрос.
На рис. 1 показано, как изменяется вероятность принадлежности испытуемого к паттерну, заданному для него в имитационной модели, в зависимости от количества выполненных заданий для двух разных алгоритмов выбора очередного вопроса – детерминированного и адаптивного. В детерминированном алгоритме тестовые задания различного уровня трудности по каждой компетенции, относящиеся к различным типам, следуют в фиксированном порядке. В адаптивном алгоритме тип каждого следующего задания в тесте выбирается из условия максимума его информационной функции для паттерна, имеющего максимум вероятности на текущем шаге алгоритма. Известно, что информационная функция по отношению к конкретному студенту максимальна для заданий, вероятность выполнения которых данным студентом близка к величине 0,5. В данном случае на k-м шаге информационная функция задания, имеющего тип m, рассчитывалась как сумма по всем паттернам произведений вероятностей правильного и неправильного ответов студента, относящегося к соответствующему паттерну, на весовой коэффициент, равный вероятности его принадлежности к данному паттерну.
,
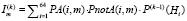m = 1…64. (6)
Тип k-го вопроса (m) выбирался исходя из максимума величины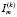 
.
Хорошим индикатором процесса уточнения принадлежности испытуемого к паттернам является энтропия распределения их вероятностей, рассчитываемая по формуле Шеннона:
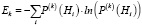, (7)
где Ek – энтропия, вычисленная после выполнения задания k.
На рис. 1 показано, как изменяется энтропия распределения вероятностей по паттернам для двух рассматриваемых алгоритмов выбора вопроса.
Приведенные на рис. 1 кривые показывают, что в случае адаптивного алгоритма выбора вопроса вероятность принадлежности испытуемого к заданному для него паттерну быстро растет и достигает максимального значения более 0,7 к двадцатому заданию. Для детерминированного алгоритма выбора вопроса эта вероятность растет значительно медленнее и даже после сорокового задания не превышает значения 0,4. Значение энтропии в первом случае уменьшается к двадцатому заданию в три раза (от 5,7 до 1,7), а во втором случае к сороковому вопросу менее чем в два раза (от 5,9 до 3,2).
Одной из проблем применения метода Байеса в данной задаче является низкая устойчивость алгоритма к случайным вариантам ответов испытуемого.
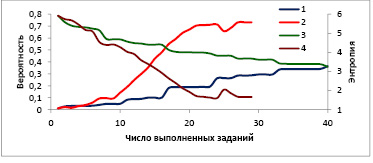
Рис. 1. Вероятность принадлежности к выбранному паттерну и изменение энтропии оценки 1, 2 – вероятность, 3, 4 – энтропия; алгоритмы: 1, 3 – детерминированный, 2, 4 – адаптивный
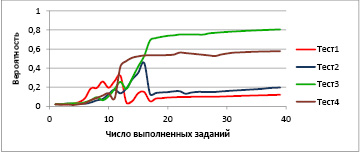
Рис. 2. Зависимость вероятности принадлежности студента заданному для него паттерну от числа выполненных заданий при нескольких имитациях процесса тестирования
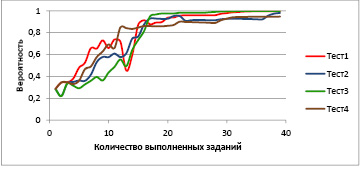
Рис. 3. Зависимость вероятности принадлежности кластеру паттернов, лежащих в окрестности заданного при тех же имитациях процесса тестирования (рис. 2)
Так как каждое задание выбирается исходя из максимума информационной функции для текущего измеренного значения уровня подготовленности студента, то вероятность правильного ответа на каждый вопрос будет близка к значению 0,5. Поэтому при неоднократном повторении имитационного теста для одного и того же студента будут наблюдаться разные варианты ответов на одни и те же типы вопросов, что повлияет на результаты измерения вероятностей принадлежности к паттернам. При этом особенно сильно на результаты измерений оказывают ответы на первые 10–15 вопросов в тесте.
На рис. 2 показано, как изменяется измеренная вероятность принадлежности к паттерну (θ1 = 1, θ2 = 1, θ3 = 1) для студента, принадлежащего этому паттерну, в зависимости от количества выполненных заданий на одной и той же последовательности вопросов по результатам четырех тестов.
Хорошо видно, что в зависимости от вариантов ответов на первые 15 вопросов байесовская вероятность изменяется по разным сценариям и последующие вопросы слабо влияют на итоговый результат измерения. Причиной такой неустойчивости является особенность самого алгоритма Байеса, который становится излишне чувствительным к случайным факторам, влияющим на результат выполнения задания. Отметим, что такие же проблемы проявляются и при традиционном приеме экзаменов.
Одним из путей повышения устойчивости алгоритма является разумное снижение требований к точности оценки. На рис. 3 показано, как изменяется вероятность принадлежности этого же студента к кластеру из паттернов, попадающих в окрестность заданного для него паттерна радиусом 2,5 логита, что соответствует ошибке измерения в один балл по одной из трех компетенций.
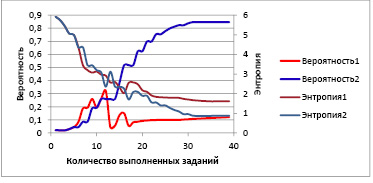
Рис. 4. Зависимость вероятности принадлежности студента заданному для него паттерну и энтропии распределения вероятностей по паттернам с регуляризацией (кривые Вероятность2, Энтропия2) и без нее (кривые Вероятность1, Энтропия1) от числа выполненных заданий
Еще одним способом повышения устойчивости алгоритма к случайным воздействиям является следующая методика. Для регуляризации результатов измерения предлагается анализировать поведение энтропии распределения вероятностей по паттернам в ходе сеанса тестирования. На рис. 4 показаны результаты измерения вероятности принадлежности студента заданному паттерну (θ1 = 1, θ2 = 1, θ3 = 1) в ходе теста 1 (кривая Вероятность1 повторяет кривую Тест1 на рис. 2) и изменение энтропии распределения вероятностей по паттернам в ходе этого теста (кривая Энтропия1). Можно заметить, что резкие изменения измеренной вероятности принадлежности студента к заданному паттерну сопровождаются «нетипичными» изменениями энтропии. Например, резкое уменьшение вероятности после тринадцатого и шестнадцатого вопроса сопровождается увеличением энтропии, хотя после каждого выполненного задания энтропия распределения вероятностей должна уменьшаться. Такое же резкое уменьшение вероятности после очередного ответа может сопровождаться резким уменьшением энтропии. То есть резкое уменьшение энтропии распределения вероятностей по паттернам или ее увеличение после очередного выполненного задания может свидетельствовать о том, что с полученным ответом не все в порядке. Для регуляризации получаемых решений предложена следующая процедура: если после выполнения очередного задания энтропия распределения вероятностей по паттернам резко уменьшается (больше чем на 20 % от текущего значения) или увеличивается, то результат выполнения данного задания не учитывается при расчете байесовской вероятности, а следующее задание, которое предъявляется студенту, имеет такие же параметры сложности, как и только что выполненное. Кривые Вероятность2 и Энтропия2 на рис. 4 показывают результаты применения предложенного алгоритма регуляризации в процессе проведения теста 1.
Видно, что применение регуляризации на основе анализа изменения энтропии распределения вероятностей по паттернам позволяет повысить устойчивость байесовского алгоритма измерения вероятности принадлежности студента к заданному паттерну. Анализ энтропии позволяет увидеть момент, когда студент дает ответ, не соответствующий тому, что от него ожидают. В этом случае мы повторяем вопрос с теми же характеристиками, что и предыдущий (как бы задаем уточняющий вопрос, если проводить аналогию с очным экзаменом). При этом количество вопросов, необходимых для оценки уровня сформированности сразу трех компетенций в ходе одного сеанса тестирования с использованием четырехбалльной шкалы оценивания, не превышает двух десятков.
Заключение
Проведенное исследование показывает, что предлагаемая модель позволяет измерять уровень сформированности нескольких компетенций (в данном случае трех) в ходе одного сеанса тестирования. Разработанная модель хорошо приспособлена к применению технологий адаптивного тестирования. Показано, что использование интеллектуальных систем выбора очередного задания совместно с байесовским алгоритмом уточнения вероятностей принадлежности испытуемого к заранее определенным паттернам позволяет значительно сократить количество заданий в тесте при заданных требованиях к результатам тестирования нескольких компетенций. А самое главное, предлагаемая модель позволяет имитировать реальный процесс очной оценки студента преподавателем, так как позволяет выявить «нелогичные» ответы испытуемого и дополнительно задать уточняющие вопросы в той же области, где возникли сомнения.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-013-00783.