В области физической культуры и спорта часто рассматриваются относительно небольшие выборки, что определяется спецификой испытуемых (высококвалифицированные спортсмены высшего эшелона). При этом научная значимость исследований в данной области подтверждается, в частности, результатами обработки статистических данных, среди которых доминируют следующие:
- первичная организация массива (ранжирование, распределение в соответствии с выбранным признаком – по возрасту, специализации, уровню сформированности какого-либо качества и прочее), определение центральных тенденций и вариационных характеристик;
- проверка значимости различий представленных выборок (контрольной и экспериментальной групп) по уровню исследуемого признака, неслучайного характера сдвигов по исследуемому показателю, несущественности отличий распределения данных от нормального закона распределения и прочее;
- выявление связи между исследуемыми факторами.
Первая и третья задачи статистического анализа решаются большинством молодых исследователей без особых трудностей. Наглядным примером является использование потенциала программного обеспечения, оптимизирующего процесс создания базы данных, реализованное сотрудниками ФГБОУ ВО «ВГАФК» при проведении исследования адаптивных возможностей организма подростков с различным уровнем здоровья и двигательной активности [1, с. 51]
В то же время проверка статистических гипотез связана с рядом проблем, обусловленных спецификой указанных исследований. Отметим, что анализ диссертационных исследователей магистрантов ФГБОУ ВО «ВГАФК» свидетельствует о том, что они предпочитают использовать в качестве средства статистической обработки данных программу MS Excel, а наиболее популярный критерий при выявлении значимых или случайных различий – критерий Стьюдента. При этом молодые ученые игнорируют тот факт, что t-критерий Стьюдента является параметрическим, то есть его применение возможно только для нормально распределенных выборок с равными дисперсиями. Возможно использование модификаций критериев, но они неизвестны широкому кругу пользователей гуманитарного направления подготовки.
В случае если для исходных данных проводится проверка гипотезы о нормальном распределении, магистранты используют критерий согласия Пирсона. При этом возникает проблема несостоятельности данного критерия согласия в связи с малым объемом данных (условия применимости – не менее 50 наблюдений). Использование потенциала MS Excel также вызывает затруднение: исследование непрерывных величин в этом случае сопряжено с необходимостью предварительного построения интервального вариационного ряда, так как частота каждой градации должна быть не менее 5.
С целью решения представленных выше проблем был произведен сравнительный анализ непараметрических критериев, используемых в современной практике статистического анализа данных малого объема.
Цель исследования: произвести сравнение условий применения непараметрических критериев для проверки гипотезы о нормальном распределении исходных данных в случае, когда выборка имеет малый объем; определить возможные несоответствия между аналитическими и графическими вариантами представления результатов сопоставления теоретического и эмпирического распределений.
Материалы и методы исследования
Исследование проводилось на основе анализа данных открытых информационных источников. Был произведен сравнительный анализ наиболее широко используемых непараметрических критериев. Рассмотрены варианты интерпретации обработки данных в формальном приложении и в виде диаграмм при помощи онлайн-калькуляторов.
Результаты исследования и их обсуждение
Вопросы выбора параметрических или непараметрических критериев для оценки различий между средними характеристиками рассматриваются рядом ученых. Одним из первых условий алгоритма отбора является проверка нормальности распределения данных [2, с. 56].
В специальной литературе приводится следующая классификация критериев согласия:
- параметрические критерии;
- критерии, основу которых составляет сравнение параметрических и непараметрических выборочных оценок;
- критерии, предусматривающие сравнение нормального распределения и эмпирических функций распределения выборочных данных [3, с. 83]
Обзор критериев согласия, применяемых в исследованиях в сфере образования, также представлен в публикациях отечественных ученых. Производится сравнение мощности следующих непараметрических критериев: Хегази – Грина, Гири, Дэвида – Хартли – Пирсона, Шпигельхальтера, Локка – Спурье, Оя. Два последних представляют собой аппроксимации критерия согласия Пирсона. Критерий Шпигельхальтера имеет существенные ограничения, а критерий Гири имеет меньшую мощность, чем критерий Шапиро – Уилка, при работе с малыми выборками [4, с. 208].
В общем случае, для нормально распределенного массива данных должны выполняться следующие условия:
1) незначительное различие или совпадение значений средней выборочной, моды и медианы;
2) соблюдение правила «трёх сигм» (интервал М ± 1σ включает не менее 68,3 % значений, представленных в выборке, интервал М ± 2σ – не менее 95,5 %, интервал М ± 3σ –не менее 99,7 % данных);
3) анализу подвергаются количественные данные;
4) положительные результаты проверки на нормальность распределения при помощи специальных критериев – Колмогорова – Смирнова или Шапиро – Уилка;
5) абсолютные значения показателей асимметрии и эксцесса не превышают 1.
Как указано выше, для проверки гипотезы о нормальном распределении полученных данных малого объема в настоящее время широко применяются критерии Шапиро – Уилка и Колмогорова – Смирнова. Условия их применимости представлены в таблице.
Ограничения применимости непараметрических критериев для проверки нормальности распределения признака
|
Критерий |
Объем выборки |
Примечание |
|
Шапиро – Уилка |
Менее 50 наблюдений |
Наиболее мощный из непараметрических критериев |
|
Колмогорова – Смирнова |
Не менее 50 наблюдений |
Имеет модификацию – критерий Лилиефорса |
Диапазон применимости критерия Шапиро – Уилка довольно широк (от 3 до 2000 наблюдений), но его надежность подтверждена для выборок объемом от 8 до 50 наблюдений. В случае если объем выборки превышает 50, возникает риск отклонить верную гипотезу о нормальности распределения. В этом случае, согласно данным таблицы, можно воспользоваться модифицированным критерием Шапиро – Уилка или критерием Колмогорова – Смирнова, имеющим меньшую мощность. Заметим, что указанные критерии сопоставляют фактическое распределение с теоретическим, не связанным с данным. Модифицированный критерий Лилиефорса предполагает построение теоретической кривой, параметры которой определены на основе анализа исходных данных, то есть наблюдается аппроксимация наблюдаемой и теоретической кривых. Данный факт снижает мощность критерия Лилиефорса, так как результаты расчетов представляют искусственно уменьшенные значения отклонений.
При использовании критериев Шапиро – Уилка и Колмогорова – Смирнова определяется значение уровня значимости (р), которое сравнивается с заданным (a). В большинстве случаев значение a принимают равным 0,05. Если расчетное значение будет ниже 0,05, то нулевая гипотеза отклоняется (данные не имеют нормального распределения).
Рассматривая последовательность проверки гипотезы, авторы трудов в данной области подчеркивают необходимость графической интерпретации (например, квантильных диаграмм). Данное требование обусловлено несовершенством анализа: при небольшом объеме наблюдений могут быть проигнорированы выраженные отклонения от нормального распределения. Большие выборки могут быть не идентифицированы, как имеющие нормальное распределение даже при наличии несущественных отклонений от теоретической модели.
Использование программных сред для реализации аналитической статистики непрерывных данных широко обсуждается в научной литературе. Авторы подчеркивают необходимость использования непараметрических критериев в случаях, когда не выполняется ряд требований, предъявляемых параметрическими методами. При этом они подчеркивают, что отказ от параметрических методов не всегда возможен или целесообразен. В этих условиях предлагается производить трансформацию (смещение) данных посредством применения возможностей программной среды R [5, с. 52].
Современные сервисы обеспечивают возможность онлайн-расчета значения критерия, а также результатов сопоставления распределений в графическом формате: присутствует возможность построения гистограмм или остаточных регрессий. Рассмотрим процедуру использования одного из онлайн-калькуляторов для расчета значений описанных критериев.
Ниже представлены итоги проверки нормального распределения результатов бега на 10 м у детей в возрасте 11 лет. Введены показатели 36 испытуемых.
Для расчета значения критерия Шапиро – Уилка были использованы возможности сервиса Shapiro-Wilk Test Calculator. Результаты были представлены как числовыми значениями (уровень значимости р, статистика W), так и графически (рис. 1).
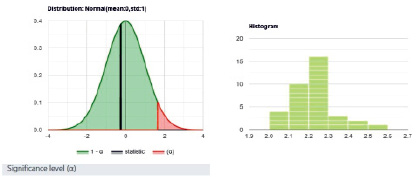
Рис. 1. Сопоставление нормального и данного (n = 36) распределения при помощи критерия Шапиро – Уилка
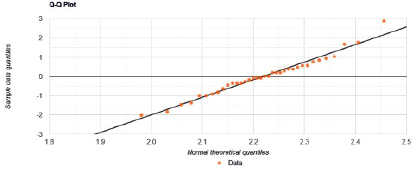
Рис. 2. Сопоставление квантилей нормального и данного распределения (n = 36)
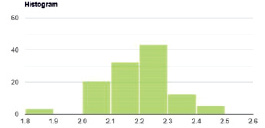
Рис. 3. Гистограмма распределения экспериментальных данных (n = 115)
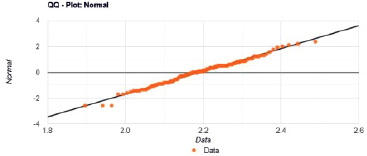
Рис. 4. Сопоставление квантилей нормального и данного распределений (n = 115)
Визуальный анализ гистограммы и сравнительный анализ квартилей теоретического нормального распределения и экспериментальных данных (рис. 2), которые были построены программой автоматически, позволяет заключить, что наблюдаются различия между сопоставляемыми распределениями, которые игнорируются даже при использовании мощного критерия.
Согласно результатам калькуляции, расчетный уровень значимости (р = 0,5962) превысил 0,05, то есть велика вероятность ошибки I рода. Тестовая статистика W равна 0,9756 и в 95 % случаев попадает в доверительный интервал [0,9398; 1]. В этих условиях нет оснований для отклонения нулевой гипотезы. Таким образом, различия между распределением экспериментальных данных и нормальным распределением не могут быть признаны существенными, данная выборка имеет нормальное распределение.
Аналогичное положение наблюдается при сопоставлении результатов бега на 10 м у детей в возрасте 10 лет. Введены показатели 115 испытуемых.
Для расчета значения критерия Колмогорова – Смирнова были использованы возможности сервиса Kolmogorov-Smirnov Test Calculator. Графическая интерпретация данных представлена в виде гистограммы (рис. 3).
Сопоставление квартилей теоретического нормального распределения и экспериментальных данных (рис. 4) свидетельствует о различиях, которые оцениваются как статистически незначимые.
Согласно полученным данным, расчетный уровень значимости (р = 0,2603) превысил 0,05, то есть велика вероятность ошибки I рода. Тестовая статистика D равна 0,0656 и в 95 % случаев попадает в доверительный интервал (–µ; 0,0829]. В этих условиях нет оснований для отклонения нулевой гипотезы. Таким образом, различия между распределением экспериментальных данных и нормальным распределением не могут быть признаны существенными, данная выборка имеет нормальное распределение.
Данное положение может частично обуславливаться более низкой, по сравнению с критерием Шапиро – Уилка, мощностью критерия Колмогорова – Смирнова. Однако такая же ситуация наблюдается более чем в 50 % произведенных проверок нормального распределения (измерения проводились в 12 группах, где состав испытуемых превышал 50 чел.).
Описанные выше несоответствия визуального анализа распределения экспериментальных данных и результатов использования непараметрических критериев различной мощности представлены в разработанных методических рекомендациях для магистрантов. В данной работе внимание студентов акцентируется на особенностях организации проверки статистических гипотез о нормальном распределении выборочных данных малого объема, в частности описана процедура отбора параметрического или непараметрического критерия согласия соответствующей мощности.
Заключение
Обоснованный отбор критерия для проверки нормального распределения выборочных данных позволяет получить корректные результаты для дальнейшего статистического анализа при проведении исследований в области физической культуры и спорта.



