Введение и постановка вопроса
Нахождение корней полиномов – одна из основных задач алгебры. К этой задаче сводятся приложения во множестве областей научных исследований. Так, к определению корней характеристических полиномов часто сводятся вычислительные методы квантовой механики и процессов колебаний [1, 2]. Часто необходимым элементом исследования является анализ устойчивости физического процесса и его дифференциальной модели. Вычисление «простых точек спектра» непосредственно сводится к нахождению корней полинома. В векторном пространстве с помощью корней характеристического полинома матрицы определяется жорданова форма линейного преобразования в ортогональном базисе, выполняется преобразование квадратичной формы к каноническому виду и исследуются геометрические объекты [3]. В приложениях теории Ляпунова корни характеристического полинома матрицы линейной системы обыкновенных дифференциальных уравнений определяют характер устойчивости системы [4]. Оценка устойчивости по первому приближению также сводится к поиску корней характеристического полинома матрицы линейной системы. Для определения устойчивости электрической цепи требуется знать расположение корней характеристического полинома на комплексной плоскости. Классический метод расчёта переходных процессов в электрических цепях опирается на свойства корней характеристического полинома. Приложения не исчерпываются этим перечислением. Однако реально находить корни полиномов сложно по причине трудоемкости вычислений и накопления погрешности, поэтому многие классические методы строятся не на прямых, а на косвенных методах определения свойств корней. Это относится к вычислению как вещественных, так и комплексных корней. В то же время надежный способ прямого вычисления корней полиномов высоких степеней мог бы упростить решения многих прикладных задач. К числу основных препятствий относят вычислительную неустойчивость, под которой понимается резкий рост погрешности значений корней в зависимости от погрешности определения полиномиальных коэффициентов [5]. Проблемой оказывается также достаточно точное определение границ области нулей и их взаимное отделение. Вычислительные трудности увеличиваются, если корни полинома отделены на малую величину [2]. Компьютерная реализация обостряет вычислительные проблемы вследствие того, что данные обрабатываются с плавающей точкой на разрядной сетке фиксированной длины, это само по себе влечет плохо контролируемое дополнительное накопление погрешности. В [6, 7] и более детально в [8, 9] предложен метод идентификации корней полинома на основе алгоритма сортировки, при этом большинство вычислительных операций заменяются на операции сравнения. Вычислительные операции требуются только для задания сравниваемых значений полиномов. В результате погрешность нахождения корней существенно снижается: как правило, сохраняются все значащие цифры мантиссы каждого корня в формате представления данных. Излагаемая ниже работа отвечает на вопрос о пределах практических ограничений метода. Путем задания высоких степеней полиномов исследуются границы числового диапазона, в которых метод сохраняет качество полноты и точности идентификации всех вещественных и комплексных корней без априорной локализации каждого корня.
Цель исследования
В работе ставится цель изложить метод компьютерной идентификации корней полиномов и указать предельные ограничения для его практического применения. В число рассматриваемых ограничений входят границы степеней полиномов в зависимости от числового диапазона компьютера, рост времени решения задачи в зависимости от степени полинома и характера взаимного расположения корней, рост погрешности идентификации корней в зависимости от возмущения коэффициентов. Исследование выполняется с помощью численных экспериментов. Указываются возможности снижения ограничений, в том числе за счет параллельной формы метода, а также формальные аспекты его применения к кодированию информации.
Об идентификации корней полиномов на основе сортировки слиянием по матрицам сравнений
Корни полинома идентифицируются как минимумы модуля этого полинома. Согласно принципу минимума модуля [10] модуль аналитической функции, отличной от константы и не обращающейся в ноль внутри области аналитичности, не может иметь локальных минимумов внутри этой области. Отсюда локальные минимумы модуля полинома достигаются в тех и только тех точках, где он обращается в ноль. Все эти локальные минимумы могут быть конструктивно идентифицированы при помощи устойчивой адресной сортировки. Метод детально изложен в [8] для случая вещественных корней полинома, в [9] – для случая комплексных корней, при этом для простоты описания использована устойчивая сортировка подсчетом по матрицам сравнений. Сортировка слиянием по матрицам сравнений применяется, однако для краткости ее описание в [8, 9] опускается. В излагаемом ниже сообщении используется только сортировка слиянием по матрицам сравнений (кратко – сортировка), поэтому для дальнейшего необходимо указать особенности ее построения и основные свойства. Сортировка упорядочивает элементы массива по отношению ≤. Пусть требуется выполнить слияние двух упорядоченных по отдельности массивов 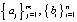 , в единый упорядоченный массив
, в единый упорядоченный массив 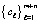 . Матрица сравнений определяется как таблица вида
. Матрица сравнений определяется как таблица вида
|
a0 |
a1 |
. . . |
am |
am+1 |
|
|
b0 |
a |
a |
. . . |
0m |
a |
|
b1 |
a |
a |
. . . |
a |
a |
|
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
|
bn |
a |
a |
. . . |
a |
a |
|
bn+1 |
a |
a |
. . . |
a |
a |
где 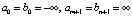 , являются формальными ограничителями, и для
, являются формальными ограничителями, и для 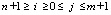 элементы таблицы определяются знаками сравнения.
элементы таблицы определяются знаками сравнения.
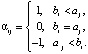
Если, например, 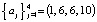 ,
, 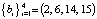 , то матрица сравнений имеет вид
, то матрица сравнений имеет вид

Ограничитель ∞ интерпретируется как элемент, заведомо больший всех упорядочиваемых элементов. Вставка элемента в окончательно упорядоченный массив определяется формулой
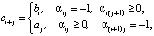 (1)
(1)
где 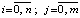 . Согласно (1) bi вставляется в качестве элемента массива ci+j тогда и только тогда, когда в i-й строке матрицы j-й элемент отрицателен, а j + 1-й элемент неотрицателен. Так, b1 = 2 перейдет в
. Согласно (1) bi вставляется в качестве элемента массива ci+j тогда и только тогда, когда в i-й строке матрицы j-й элемент отрицателен, а j + 1-й элемент неотрицателен. Так, b1 = 2 перейдет в 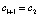 , b2 = 6 перейдет в
, b2 = 6 перейдет в 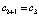 , b3 = 14 перейдет в
, b3 = 14 перейдет в 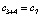 , b4 = 15 перейдет в
, b4 = 15 перейдет в 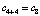 . Элемент aj вставляется в качестве элемента массива ci+j тогда и только тогда, когда в j-м столбце матрицы i + 1-й элемент отрицателен, а i-й элемент неотрицателен: a1 = 1 перейдет в
. Элемент aj вставляется в качестве элемента массива ci+j тогда и только тогда, когда в j-м столбце матрицы i + 1-й элемент отрицателен, а i-й элемент неотрицателен: a1 = 1 перейдет в 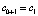 , a2 = 6 перейдет в
, a2 = 6 перейдет в 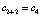 , a3 = 6 перейдет в
, a3 = 6 перейдет в 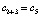 , a4 = 10 перейдет в
, a4 = 10 перейдет в 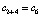 . В результате все элементы массива c будут упорядочены. Для равных элементов массивов b и a приоритет предшествования отдается элементам массива b. Для равных элементов одного массива на выходе сохраняется их входной порядок. Таким образом, слияние устойчиво. Все сравнения в матрице взаимно независимы и могут быть выполнены одновременно, вставки выполняются по сравнению каждого элемента матрицы с двумя соседями, поэтому слияние максимально параллельно и выполнимо с временной сложностью
. В результате все элементы массива c будут упорядочены. Для равных элементов массивов b и a приоритет предшествования отдается элементам массива b. Для равных элементов одного массива на выходе сохраняется их входной порядок. Таким образом, слияние устойчиво. Все сравнения в матрице взаимно независимы и могут быть выполнены одновременно, вставки выполняются по сравнению каждого элемента матрицы с двумя соседями, поэтому слияние максимально параллельно и выполнимо с временной сложностью 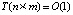 , в скобках слева – число процессорных элементов. Последовательное слияние выполняется путем обхода области неотрицательных элементов, как для данного примера отмечено стрелками – шаг сравнения – одна стрелка, указывающая на результат сравнения с элементом строки:
, в скобках слева – число процессорных элементов. Последовательное слияние выполняется путем обхода области неотрицательных элементов, как для данного примера отмечено стрелками – шаг сравнения – одна стрелка, указывающая на результат сравнения с элементом строки:
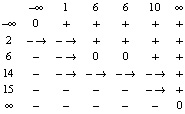
Если на шаге результат сравнения – элемент на пересечении строки и столбца матрицы – отрицательный, то делается вставка по формуле (1) элемента массива a над этим столбцом и выполняется переход к элементу следующего столбца в этой же строке. Если на шаге элемент на пересечении строки и столбца матрицы неотрицательный, то согласно (1) делается вставка элемента массива b слева от текущей строки и выполняется переход к элементу следующей строки в этом же столбце. На каждом шаге в массив c вставляется один элемент, принадлежащий либо массиву b, либо массиву a. Число шагов алгоритма равно суммарному числу элементов входных массивов. Временная сложность (здесь и ниже – число последовательных шагов алгоритма) в данном последовательном варианте 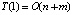 . Слияние адресное и устанавливает взаимно однозначное соответствие входных и выходных индексов элементов для каждого в отдельности входного массива. Такая организация прямой и обратной адресации сохраняется в целом для сортировки слиянием. С изложенным видоизменением слияния сортировка следует обычной схеме [11]: вначале выполняется слияние каждой пары входных элементов (с запоминанием обратных адресов), затем, аналогично, слияние упорядоченных пар, упорядоченных четверок и т.д. При этом сохраняется взаимный порядок сливаемых пар и массивов пары. Программа сортировки представлена процедурой sort, неизменной во всех приводимых ниже программах. Количество сортируемых элементов в данной модификации произвольно, освобождение от равенства степени двойки достигается имитацией дописывания до ближайшей степени двойки возрастающей последовательности элементов входного массива, заведомо больших, чем сортируемые. Имитация реализуется положительными значениями всех тех элементов каждой из матриц сравнения, которые соответствуют номерам большим истинного числа входных элементов. Сортировка не перемещает входных элементов, вызывая их на момент сравнения по обратным адресам входных индексов. При этом сами обратные адреса перемещаются, имитируя перемещение сортируемых элементов. Окончательные значения обратных адресов на выходе сортировки располагаются в отдельном массиве в соответствии порядку отсортированных элементов. Все слияния на шаге сортировки взаимно независимы и могут выполняться параллельно. Число таких шагов не превосходит логарифма ближайшей целой части количества сортируемых элементов. Максимально параллельный вариант сортировки имеет временную сложность
. Слияние адресное и устанавливает взаимно однозначное соответствие входных и выходных индексов элементов для каждого в отдельности входного массива. Такая организация прямой и обратной адресации сохраняется в целом для сортировки слиянием. С изложенным видоизменением слияния сортировка следует обычной схеме [11]: вначале выполняется слияние каждой пары входных элементов (с запоминанием обратных адресов), затем, аналогично, слияние упорядоченных пар, упорядоченных четверок и т.д. При этом сохраняется взаимный порядок сливаемых пар и массивов пары. Программа сортировки представлена процедурой sort, неизменной во всех приводимых ниже программах. Количество сортируемых элементов в данной модификации произвольно, освобождение от равенства степени двойки достигается имитацией дописывания до ближайшей степени двойки возрастающей последовательности элементов входного массива, заведомо больших, чем сортируемые. Имитация реализуется положительными значениями всех тех элементов каждой из матриц сравнения, которые соответствуют номерам большим истинного числа входных элементов. Сортировка не перемещает входных элементов, вызывая их на момент сравнения по обратным адресам входных индексов. При этом сами обратные адреса перемещаются, имитируя перемещение сортируемых элементов. Окончательные значения обратных адресов на выходе сортировки располагаются в отдельном массиве в соответствии порядку отсортированных элементов. Все слияния на шаге сортировки взаимно независимы и могут выполняться параллельно. Число таких шагов не превосходит логарифма ближайшей целой части количества сортируемых элементов. Максимально параллельный вариант сортировки имеет временную сложность 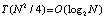 [12]. Последовательный вариант этой же сортировки оценивается временной сложностью
[12]. Последовательный вариант этой же сортировки оценивается временной сложностью 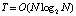 [12]. Все другие особенности применения сортировки для идентификации корней полиномов во всех деталях сохраняют описание и программную реализацию, изложенные в [8] для случая вещественных корней и в [9] – для случая комплексных корней полинома. Реализация этих особенностей неизменна во всех программах ниже. Суть применения кратко заключается в следующем. После сортировки последовательности c каждый ее локально минимальный элемент с входным индексом ek,
[12]. Все другие особенности применения сортировки для идентификации корней полиномов во всех деталях сохраняют описание и программную реализацию, изложенные в [8] для случая вещественных корней и в [9] – для случая комплексных корней полинома. Реализация этих особенностей неизменна во всех программах ниже. Суть применения кратко заключается в следующем. После сортировки последовательности c каждый ее локально минимальный элемент с входным индексом ek, 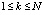 , в произвольном радиусе локализации r = ε0 идентифицируется по схеме, согласно которой
, в произвольном радиусе локализации r = ε0 идентифицируется по схеме, согласно которой
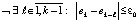 . (2)
. (2)
Фрагмент программной реализации условия (2) имеет вид
{выполнение процедуры сортировки sort}
k: = 1; while k < = n do begin for L: = 1 to k-1 do if abs(e[k]-e[k-L]) < = eps0 then goto 11; ik: = e[k];
11: k: = k+1 end;
Здесь ik – индекс локально минимального элемента в окрестности радиуса eps0 = ε0: оператор ik: = e[k]; выполняется, если входной индекс любого элемента меньшего ck располагается от ek дальше, чем на ε0, поскольку в этом случае ek – индекс локально минимального элемента в окрестности радиуса ε0. Если входной индекс хотя бы одного элемента меньшего ck расположен ближе, чем на ε0, от ek, элемент ck не является минимальным в окрестности радиуса ε0 и пропускается путем перехода по метке к следующему номеру k. На вход сортировки с шагом дискретизации h поступают значения модуля полинома. По принципу минимума модуля в результате выполнения (2) в окрестности радиуса ε0 окажется один и только один корень в некотором приближении. К нему выполняется спуск посредством итеративного сужения диаметра окрестности локализованного приближения до сближения концов диаметра ниже заданной границы абсолютной погрешности.
Реализующая изложенный подход программа без изменения заимствуется из [8]:
program ITERREKORN1680;
{$APPTYPE CONSOLE} uses SysUtils;
const n1 = 40; b: array [1..n1] of extended = (1, 1.0001, 2, 2.0001, 3, 3.0001, 4, 4.0001, 5, 5.0001, 6, 6.0001, 7,
7.0001, 8, 8.0001, 9, 9.0001, 10, 10.0001, 11, 11.0001, 12, 12.0001, 13, 13.0001, 14, 14.0001, 15, 15.0001, 16,
16.0001, 17, 17.0001, 18, 18.0001, 19, 19.0001, 20, 20.0001);
eps = 1E-44; n00 = 1512; mm = 4; type vect1 = array [0..4*n00] of extended; vect2 = array [0..4*n00] of longint;
vec = array [0..n1] of extended; var i,j,k,l,ee,nn0,kk,kk1: longint; a,c: vect1; e: vect2; rex:vect1;
aaa,x,x0,x1,xk,xk0,xk1,h0,min,eps1,hh,z,z1,x00,x11,eps0,h,eps00: extended;
procedure sort(var nn0:longint; var c: vect1; var e: vect2);
type vecc = array[0..4*n00] of longint; var ab:integer; i,j,k,l,m,r,nm,p,n: longint; e1,e2: vecc;
begin p : = trunc(ln(nn0)/ln(2)); if p<> ln(nn0)/ln(2) then p : = p+1; n : = round(exp(p*ln(2)));
for l : = 1 to n do if l< = nn0 then e[l] : = l else ab: = 1; for r : = 1 to p do begin m : = round(exp(r*ln(2)));
nm: = n div m; for k : = 0 to nm-1 do begin for l : = 1 to m div 2 do begin
if (k * m + l > nn0) or (e[k * m + l]>nn0) then ab : = l else e1[l] : = e[k * m + l];
if (k * m + m div 2+ l > nn0) or (e[k * m + m div 2+ l]>nn0) then ab : = 1
else e2[l] : = e[k * m + m div 2 + l] end; i : = 1; j : = 0; while i + j < = m do begin
if i = m div 2 + 1 then ab : = -1; if j = m div 2 then ab : = 1;
if (k * m + i > nn0) or (e[k * m + i]>nn0) or (k * m + m div 2 + j > nn0-1) or (e[k * m + m div 2+ j]>nn0)
then ab: = 1; if (i < = m div 2) and (j < = m div 2 -1) and (k * m + i< = nn0) and (k * m + m div 2 + j < = nn0-1)
then if (e2[j + 1] > nn0) or (e1[i]> nn0) then ab : = 1 else
begin if c[e2[j + 1]] - c[e1[i]] = 0 then ab : = 0; if c[e2[j + 1]] - c[e1[i]]> 0 then ab : = 1;
if c[e2[j + 1]] - c[e1[i]]< 0 then ab : = -1 end; if ab > = 0 then begin e[k * m + i + j] : = e1[i]; i : = i + 1 end
else begin e[k * m + i + j] : = e2[j + 1]; j : = j + 1 end end end end end;
procedure ident (var x00,x11,eps0, h: extended);
label 21, 22;
{polinom stepeni 1680}
function func (var x: extended): extended;
var i0,i1,i2: integer; p,p0,p1: extended;
begin p: = 1; for i0: = 1 to n1 do p: = p*(sqr(x)-sqr(b[i0]));
p1: = 1; for i1: = 1 to n1 do for i2: = 1 to 10 do p1: = p1*(sqr(x)-sqr(b[i1]+i2*0.001));
p0: = 1; for i1: = 1 to n1 do for i2: = 1 to 10 do p0: = p0*(sqr(x)-sqr(b[i1]-i2*0.001));
func: = abs(p*p1*p0); end;
procedure min1 (var x: extended;var ee:longint);
begin min: = func(x); ee: = 0; for i: = 1 to mm do begin
x: = xk0+i*h0; if min > func(x) then begin min: = func(x); ee: = i; end;end;end;
begin
aaa: = 1e62; nn0: = n00; hh: = nn0*h; kk: = 0; x0: = x00; while x0 < = x11 do begin
for i: = 1 to nn0 do begin x: = x0+i*h; c[i]: = func(x); end;
sort(nn0, c, e); k: = 1; while k< = nn0 do begin for l : = 1 to k-1 do
if abs(e[k]-e[k-l]) < = eps0/h then goto 22; xk: = x0+e[k]*h; eps1: = eps0;xk0: = xk-eps1;
xk1: = xk+eps1;h0: = abs(2*eps1)/mm; while abs(eps1) > eps do begin x: = xk0; min1(x,ee); eps1: = eps1/1.2;
xk0: = xk0+ee*h0-eps1; xk1: = xk0+ee*h0+eps1; h0: = abs(2*eps1)/mm; end; if func(xk) = 0 then begin x: = xk;
goto 21; end; x: = xk0+ee*h0+eps1;
for i: = 1 to 2 do begin z: = x+i*h; if func(x) > = func(z) then goto 22; end;
for i: = 1 to 2 do begin z1: = x-i*h; if func(x) > = func(z1) then goto 22; end;
if abs(aaa-x)< = 1e-20 then goto 22;
21: writeln (' ', x,' ', func(x)); aaa: = x; kk: = kk+1; rex[kk]: = x;
22: k: = k+1 end; x0: = x0 + hh end; end;
begin writeln ('PRIBLIJENIE'); writeln; x00: = -32; x11: = 32; eps0: = 0.00049/2; h: = eps0/43; eps00: = eps0;
ident(x00,x11,eps0, h); writeln; writeln ('TOCHN'); writeln; eps0: = eps0/10; h: = eps0/43; for kk1: = 1 to kk do
begin x00: = rex[kk1]-eps00; x11: = rex[kk1]+eps00; ident(x00,x11,eps0, h); end; readln; end.
Единственное изменение состоит в способе задания полинома, что детально оговаривается ниже. Программа построена на первоначальной локализации корней с относительно большим радиусом локализации, по ходу которой каждый локализованный корень запоминается. В окрестности каждого запомненного корня, ограниченной исходным радиусом локализации, выполняется повторный запуск всей процедуры с радиусом локализации столь малым, что он гарантирует идентификацию всех (возможно пропущенных при первоначальной локализации) корней полинома. Начальный радиус локализации меньше половины наименьшего расстояния между корнями, шаг дискретизации около 0,02 радиуса, эти величины могут быть уменьшены или увеличены в зависимости от характера задачи.
Границы применимости метода в случае вещественных корней полинома
Цель экспериментов – идентификация корней полиномов высоких степеней. С этой целью на вход программ подаются специально подобранные значения корней, чтобы на выходе визуально контролировать наличие корней и точность их идентификации. В данном примере на вход программы ITERREKORN1680 поступают элементы массива b, где они попарно отделены на 0,0001. В разделе описаний процедуры ident из элементов массива b формируется входной полином с помощью подпрограммы func. По основной теореме высшей алгебры полином
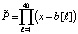 (3)
(3)
имел бы в качестве корней все 40 элементов массива b. Для увеличения степени полинома, корни которого требуется найти, полином (3) преобразовывался в полином степени 80:
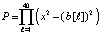 . (4)
. (4)
У полинома (4) те же корни, что и у полинома (3), но кроме того в число корней входят все корни (3) с обратным знаком. Дальнейшее увеличение степени обеспечивает алгоритм
p1: = 1; for i1: = 1 to n1 do for i2: = 1 to 10 do p1: = p1*(sqr(x)-sqr(b[i1]+i2*0.01));
p0: = 1; for i1: = 1 to n1 do for i2: = 1 to 10 do p0: = p0*(sqr(x)-sqr(b[i1]-i2*0.01)); (5)
В первом цикле алгоритм (5) к каждому корню полинома (4) десять раз добавляет по 0.01, образуя новые корни, и перемножает все разности квадратов независимой переменной и значения нового корня. Получается полином степени 800. Во втором цикле от каждого корня полинома (4) вычитается по 0,01, и полученные биномы аналогично перемножаются. Получается еще один полином степени 800. Затем значению func присваивается произведение всех трех полиномов: func: = abs(p*p1*p0); В результате на вход программы поступает полином степени 1680, многие корни которого взаимно отделены на 0,0001. Результат работы программы (в колонке слева – значения корней, справа – соответственные значения полинома):
-2.01001000000000E+0001 0.00000000000000E+0000
-2.01000000000000E+0001 0.00000000000000E+0000
-2.00900000000000E+0001 0.00000000000000E+0000
-2.00901000000000E+0001 0.00000000000000E+0000
-2.00801000000000E+0001 0.00000000000000E+0000
-2.00800000000000E+0001 0.00000000000000E+0000
………………………………………………………….
-2.00101000000000E+0001 0.00000000000000E+0000
-2.00100000000000E+0001 0.00000000000000E+0000
-2.00000000000000E+0001 0.00000000000000E+0000
-2.00001000000000E+0001 0.00000000000000E+0000
-1.99900000000000E+0001 0.00000000000000E+0000
…………………………………………………………
1.99801000000000E+0001 0.00000000000000E+0000
1.99800000000000E+0001 0.00000000000000E+0000
1.99901000000000E+0001 0.00000000000000E+0000
1.99900000000000E+0001 0.00000000000000E+0000
2.00000000000000E+0001 0.00000000000000E+0000
2.00001000000000E+0001 0.00000000000000E+0000
2.00100000000000E+0001 0.00000000000000E+0000
2.00101000000000E+0001 0.00000000000000E+0000
2.00201000000000E+0001 0.00000000000000E+0000
2.00200000000000E+0001 0.00000000000000E+0000
…………………………………………………………
2.00800000000000E+0001 0.00000000000000E+0000
2.00801000000000E+0001 0.00000000000000E+0000
2.00800000000000E+0001 0.00000000000000E+0000
2.00900000000000E+0001 0.00000000000000E+0000
2.00901000000000E+0001 0.00000000000000E+0000
2.01000000000000E+0001 0.00000000000000E+0000
2.01001000000000E+0001 0.00000000000000E+0000
Для полиномов степени не выше 100 достаточно было бы взять радиус локализации меньше половины расстояния между ближайшими корнями [8]. Однако с ростом степени растет число операций с плавающей точкой, что влечет накопление погрешности значения полинома. Это приводит к необходимости уменьшить радиус локализации до значений, представленных в разделе инструкций. Согласно проверке найдены все 1680 корней, которые вычислены без потери значащих цифр мантиссы в формате представления данных.
Замечание 1. Ненакопление погрешности достигается потому, что сортировка не преобразует входные значения, а только сравнивает их. Аналогично, при реализации схемы (2) используются только сравнения индексов, и в остальном программа построена на сравнении значений. Потеря точности возникает на входе, при вычислении значения полинома, что с ростом его степени может нарушать границы числового диапазона компьютера.
Замечание 2. Все корни без изменений нашлись бы в расширенной области, например, на отрезке x00: = -322; x11: = 322. Однако это замедлило бы работу программы. В представленном варианте на ПК с процессором Intel(R) Core(TM) i5-4460 CPU@3.20GHz программа выполняется 4 мин. Дальнейшие эксперименты направлены на кратное увеличение степени полинома, поэтому не безразлично, вычисляется ли значение полинома от 322 или от 22. В первом случае он быстрее выйдет из допустимого числового диапазона, и определить применимость метода для испытываемой степени полинома уже не удастся.
Замечание 3. Чтобы найти приближенные границы области корней полинома, следует решить задачу в расширенных границах с увеличенным радиусом локализации, например, eps0: = 0.0049; h: = eps0/43. Это даст быстрое решение с пропуском близко расположенных корней, но четко обозначит границы области корней в процессе вывода данных [8].
Если в циклах (5)0,01 заменить на 0,01/2, то выходные данные по-прежнему сохранят наглядность контроля, в частности при двойном увеличении числа шагов цикла:
p1: = 1; for i1: = 1 to n1 do for i2: = 1 to 20 do p1: = p1*(sqr(x)-sqr(b[i1]+i2*0.01/2));
p0: = 1; for i1: = 1 to n1 do for i2: = 1 to 20 do p0: = p0*(sqr(x)-sqr(b[i1]-i2*0.01/2)); (6)
С циклами (6) вместо (5) та же программа (без каких-либо других изменений) будет искать корни полинома степени 3280. Результат работы программы:
-2.01000000000000E+0001 0.00000000000000E+0000
-2.01001000000000E+0001 0.00000000000000E+0000
-2.00950000000000E+0001 0.00000000000000E+0000
-2.00951000000000E+0001 0.00000000000000E+0000
-2.00900000000000E+0001 0.00000000000000E+0000
-2.00901000000000E+0001 0.00000000000000E+0000
-2.00851000000000E+0001 0.00000000000000E+0000
-2.00850000000000E+0001 0.00000000000000E+0000
-2.00801000000000E+0001 0.00000000000000E+0000
-2.00800000000000E+0001 0.00000000000000E+0000
………………………………………………………….
2.00800000000000E+0001 0.00000000000000E+0000
2.00801000000000E+0001 0.00000000000000E+0000
2.00851000000000E+0001 0.00000000000000E+0000
2.00850000000000E+0001 0.00000000000000E+0000
2.00900000000000E+0001 0.00000000000000E+0000
2.00901000000000E+0001 0.00000000000000E+0000
2.00950000000000E+0001 0.00000000000000E+0000
2.00951000000000E+0001 0.00000000000000E+0000
2.01000000000000E+0001 0.00000000000000E+0000
2.01001000000000E+0001 0.00000000000000E+0000
Согласно проверке найдены все корни полинома степени 3280 без потери значащих цифр.
Замечание 4. Препятствием увеличения степени полинома является ограниченность числового диапазона компьютера. Так, если непосредственно повторить прием (6) для последующего двойного увеличения степени, то программа выйдет из числового диапазона.
Чтобы обойти трудность, в представление входного полинома вносится деление на одно и то же число независимой переменной и значения корня, например,
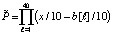 . (7)
. (7)
Значения корней полинома при этом не изменятся, но значение самого полинома уменьшится в 1040, что отдалит его значение от границ числового диапазона. Вся подпрограмма задания полинома степени 6480 примет вид
function func (var x: extended): extended;
var i0,i1,i2: integer; p,p0,p1: extended;
begin p: = 1; for i0: = 1 to n1 do p: = p*(sqr(x/10)-sqr(b[i0]/10));
p1: = 1; for i1: = 1 to n1 do for i2: = 1 to 40 do p1: = p1*(sqr(x/10)-sqr((b[i1]+i2*0.01/2/2)/10));
p0: = 1; for i1: = 1 to n1 do for i2: = 1 to 40 do p0: = p0*(sqr(x/10)-sqr((b[i1]-i2*0.01/2/2)/10));
func: = abs(p*p1*p0); end;
Других изменений в программу ITERREKORN1680 не вносится. Результат работы программы:
-2.01001000000000E+0001 0.00000000000000E+0000
-2.01000000000000E+0001 0.00000000000000E+0000
-2.00925000000000E+0001 0.00000000000000E+0000
-2.00926000000000E+0001 0.00000000000000E+0000
-2.00950000000000E+0001 0.00000000000000E+0000
-2.00951000000000E+0001 0.00000000000000E+0000
-2.00876000000000E+0001 0.00000000000000E+0000
-2.00875000000000E+0001 0.00000000000000E+0000
-2.00900000000000E+0001 0.00000000000000E+0000
-2.00901000000000E+0001 0.00000000000000E+0000
…………………………………………………………..
2.00876000000000E+0001 0.00000000000000E+0000
2.00875000000000E+0001 0.00000000000000E+0000
2.00900000000000E+0001 0.00000000000000E+0000
2.00901000000000E+0001 0.00000000000000E+0000
2.00925000000000E+0001 0.00000000000000E+0000
2.00926000000000E+0001 0.00000000000000E+0000
2.00950000000000E+0001 0.00000000000000E+0000
2.00951000000000E+0001 0.00000000000000E+0000
2.00975000000000E+0001 0.00000000000000E+0000
2.00976000000000E+0001 0.00000000000000E+0000
2.01000000000000E+0001 0.00000000000000E+0000
2.01001000000000E+0001 0.00000000000000E+0000
По мере достоверности визуальной проверки можно утверждать, что программа идентифицировала все 6480 корней полинома степени 6480 без потери значащих цифр мантиссы в формате представления данных. Программа выполняется примерно 1 ч 30 мин.
Если пытаться еще раз повторить прием (7) для удвоения степени полинома, то его значение выйдет за пределы числового диапазона. Чтобы этого избежать, использовано следующее видоизменение приема:
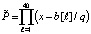 , (8)
, (8)
то есть делению подверглись непосредственно значения самих корней. Из возможных значений делителя не выйти из числового диапазона удалось только при q = 18 и q = 17. Использование (8) сокращает размер области корней полинома в q раз. Поэтому необходимо в q раз уменьшить модуль ранее заданных границ. Расстояние между корнями аналогично уменьшится, – необходимо в q раз уменьшить радиус локализации, уменьшится модуль корней, при выводе нужно умножить их значения на q. В итоге подпрограмма func примет вид
function func (var x: extended): extended;
var i0,i1,i2: integer; p,p0,p1: extended;
begin p: = 1; for i0: = 1 to n1 do p: = p*(sqr(x)-sqr(b[i0]/18));
p1: = 1; for i1: = 1 to n1 do for i2: = 1 to 80 do p1: = p1*(sqr(x)-sqr((b[i1]+i2*0.01)/18));
p0: = 1; for i1: = 1 to n1 do for i2: = 1 to 80 do p0: = p0*(sqr(x)-sqr((b[i1]-i2*0.01)/18)); func: = abs(p*p1*p0); end;
От деления добавлявшихся к исходным корням значений (/2/2/2) пришлось отказаться, при его использовании программа выходила из числового диапазона. С изменением вывода корней, границ области и радиуса локализации заключительная часть программы примет вид
…………………………………………………………………
21: writeln (' ', 18*x,' ', func(x)); aaa: = x; kk: = kk+1; rex[kk]: = x;
22: k: = k+1 end; x0: = x0 + hh end; end;
begin writeln (''PRIBLIJENIE'); x00: = -22/18; x11: = 22/18; eps0: = 0.00049/2/2/18; h: = eps0/43; eps00: = eps0;
ident(x00,x11,eps0,h); writeln ('TOCHN'); eps0: = eps0/10/2; h: = eps0/43; for kk1: = 1 to kk do
begin x00: = rex[kk1]-eps00; x11: = rex[kk1]+eps00; ident(x00,x11,eps0, h); end; readln; end.
Других изменений в программу ITERREKORN1680 не вносилось. Результат работы программы:
-2.08001000000000E+0001 0.00000000000000E+0000
-2.08000000000000E+0001 0.00000000000000E+0000
…………………………………………………………..
2.07001000000000E+0001 0.00000000000000E+0000
2.07000000000000E+0001 0.00000000000000E+0000
2.07101000000000E+0001 0.00000000000000E+0000
2.07100000000000E+0001 0.00000000000000E+0000
2.07201000000000E+0001 0.00000000000000E+0000
2.07200000000000E+0001 0.00000000000000E+0000
2.07300000000000E+0001 0.00000000000000E+0000
2.07301000000000E+0001 0.00000000000000E+0000
2.07400000000000E+0001 0.00000000000000E+0000
2.07401000000000E+0001 0.00000000000000E+0000
2.07501000000000E+0001 0.00000000000000E+0000
2.07500000000000E+0001 0.00000000000000E+0000
2.07601000000000E+0001 0.00000000000000E+0000
2.07600000000000E+0001 0.00000000000000E+0000
2.07701000000000E+0001 0.00000000000000E+0000
2.07700000000000E+0001 0.00000000000000E+0000
2.07800000000000E+0001 0.00000000000000E+0000
2.07801000000000E+0001 0.00000000000000E+0000
2.07900000000000E+0001 0.00000000000000E+0000
2.07901000000000E+0001 0.00000000000000E+0000
2.08001000000000E+0001 0.00000000000000E+0000
2.08000000000000E+0001 0.00000000000000E+0000
По мере достоверности проверки без потери значащих цифр найдены все корни полинома степени 12880, включая отделенные на 0,0001. Программа выполняется 2 ч 15 мин.
Замечание 5. Данные варианты программ не идентифицируют кратность корней полинома, – повторный вывод одинаковых значений не означает кратность. Вариант программы с учетом кратности приводится в [9].
Прием (8) сужения области корней полинома можно распространить на случай, когда полином задан своими коэффициентами,
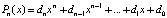 , (9)
, (9)
где, не умаляя общности, можно считать dn = 1. Корни полинома (9) связаны с его коэффициентами формулами Виета:
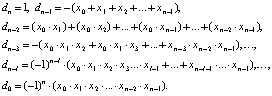 (10)
(10)
Из (9), (10) следует, что каждый из корней поделится на число q > 0 тогда и только тогда, когда каждый 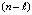 -й коэффициент
-й коэффициент 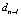 поделится на
поделится на 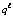 ,
, 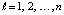 .
.
С сохранением приема степень полинома можно еще немного увеличить. По сравнению с последним вариантом программы следует ввести изменение, состоящее в увеличении количества шагов внутреннего цикла в подпрограмме func до 90 и взять q = 17,
function func (var x: extended): extended;
var i0,i1,i2: integer; p,p0,p1: extended;
begin p: = 1; for i0: = 1 to n1 do p: = p*(sqr(x)-sqr(b[i0]/17));
p1: = 1; for i1: = 1 to n1 do for i2: = 1 to 90 do p1: = p1*(sqr(x)-sqr((b[i1]+i2*0.01)/17));
p0: = 1; for i1: = 1 to n1 do for i2: = 1 to 90 do p0: = p0*(sqr(x)-sqr((b[i1]-i2*0.01)/17)); func: = abs(p*p1*p0); end;
при выводе значений учитывать q = 17, радиус локализации в уточняющей части раздела инструкций ('TOCHN') следует изменить в сторону уменьшения,
21: writeln (' ', 17*x,' ', func(x)); aaa: = x; kk: = kk+1; rex[kk]: = x;
22: k: = k+1 end; x0: = x0 + hh end; end;
begin writeln ('PRIBLIJENIE'); x00: = -22/17; x11: = 22/17; eps0: = 0.00049/2/2/17; h: = eps0/43;
eps00: = eps0; ident(x00,x11,eps0,h); writeln ('TOCHN'); eps0: = eps0/10/17; h: = eps0/43;
for kk1: = 1 to kk do begin x00: = rex[kk1]-eps00; x11: = rex[kk1]+eps00; ident(x00,x11,eps0,h); end; readln; end.
С точностью до визуальной проверки результатом работы программы станет идентификация всех корней полинома степени 14480 без потери значащих цифр мантиссы:
-2.09000000000000E+0001 0.00000000000000E+0000
-2.09001000000000E+0001 0.00000000000000E+0000
…………………………………………………………..
2.08000000000000E+0001 0.00000000000000E+0000
2.08001000000000E+0001 0.00000000000000E+0000
2.08100000000000E+0001 0.00000000000000E+0000
2.08101000000000E+0001 0.00000000000000E+0000
2.08200000000000E+0001 0.00000000000000E+0000
2.08201000000000E+0001 0.00000000000000E+0000
…………………………………………………………
2.08700000000000E+0001 0.00000000000000E+0000
2.08701000000000E+0001 0.00000000000000E+0000
2.08800000000000E+0001 0.00000000000000E+0000
2.08801000000000E+0001 0.00000000000000E+0000
2.08900000000000E+0001 0.00000000000000E+0000
2.08901000000000E+0001 0.00000000000000E+0000
2.09000000000000E+0001 0.00000000000000E+0000
2.09001000000000E+0001 0.00000000000000E+0000
Программа выполняется 3 ч 20 мин. Дальнейшие попытки увеличить степень полинома приводили к выходу из границ числового диапазона или к потере значащих цифр мантисс корней. На этом численные эксперименты в данном направлении были завершены.
О влиянии возмущения коэффициентов полинома на идентификацию вещественных корней
Алгоритмы вычисления корней полинома принято считать неустойчивыми: независимо от способа нахождения корней на их значения крайне влияет возмущение коэффициентов полинома. В [5] приводится пример, когда коэффициент полинома
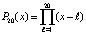 , (11)
, (11)
при x19 возмущается на 2–23, –
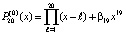 , (12)
, (12)
β19 = 2–23, – в результате больше половины корней полинома (12) становятся комплексными, один из остальных отличается от соответственного корня (11) уже в первых знаках после десятичной точки. Это полностью подтверждается идентификацией корней (12) по представленной выше программе, где подпрограмма func примет вид
function func (var x: extended): extended;
var i1: 1..n1; p: extended;
begin p: = 1; for i1: = 1 to 20 do p: = p*(x-i1); func: = abs(p+sqr(sqr(sqr(sqr(x))))*x*x*x*exp(-23*ln(2))); end;
раздел инструкций берется с параметрами границ области корней и радиусов локализации:
begin writeln (' ':12,'PRIBLIJENIE'); writeln; writeln;
x00: = -22; x11: = 22; eps0: = 0.00049; h: = eps0/43; eps00: = eps0; ident(x00,x11,eps0, h); writeln; writeln;
writeln (' ':12,'TOCHN'); writeln; writeln; eps0: = eps0/10; h: = eps0/43; for kk1: = 1 to kk do
begin x00: = rex[kk1]-eps00; x11: = rex[kk1]+eps00; ident(x00,x11,eps0, h); end; readln; end.
Результат работы программы:
1.00000000000000E+0000 1.19209289550781E-0007
2.00000000000000E+0000 2.67926726706873E-0005
3.00000000000019E+0000 5.58171556354209E-0005
3.99999999973898E+0000 2.90234767774677E-0006
5.00000007244851E+0000 1.26962299873412E-0006
5.99999305644644E+0000 1.58001785166561E-0006
7.00030339886563E+0000 9.00123268365860E-0007
7.99302504437346E+0000 3.68803739547729E-0007
9.14728137862023E+0000 2.23517417907715E-0007
9.50201129715976E+0000 5.96046447753906E-0008
Однако при уменьшении возмущения рассматриваемого коэффициента до β19 = 2–33 уже все 20 корней станут вещественными, а при β19 = 2–43 все корни идентифицируются с точностью до 0.5×10–4. Дальнейшее уменьшение возмущения влечет повышение точности приближения к значениям корней из (1), и при β19 = 2–89 все корни окажутся найденными с верными значащими цифрами в принятом числовом формате [7]. Более того, даже если все коэффициенты полинома (11) (кроме старшего единичного) возмутить, причем на возрастающие значения по убыванию индекса коэффициента, вплоть до возмущений больших единицы в коэффициентах при степенях от четвертой до нулевой,
function func (var x: extended): extended;
var i1: 1..n1;p:extended;
begin p: = 1; for i1: = 1 to 20 do p: = p*(x-i1); func: = abs(p+1e-27*(sqr(sqr(sqr(sqr(x))))*x*x*x)+
1e-26*(sqr(sqr(sqr(sqr(x))))*x*x)+1e-25*(sqr(sqr(sqr(sqr(x))))*x)+1e-24*(sqr(sqr(sqr(sqr(x))))))+
1e-22*((sqr(sqr(sqr(x))))*x*x*x -1e-20*(sqr(sqr(sqr(x))))*x*x-1e-18*(sqr(sqr(sqr(x))))*x-
1e-16*(sqr(sqr(sqr(x))))-1e-12*((sqr(sqr(x))))*x*x*x-1e-8*((sqr(sqr(x))))*x*x-1e-4*((sqr(sqr(x))))*x-
1*sqr(sqr(x))-1.4*sqr(x)*x-1.8*sqr(x)-2.2*x-2.6); end;
все значения корней полинома совпадут с корнями невозмущенного полинома (11) при идентификации по представленной программе:
1.00000000000000E+0000 -7.98899001000100E-0022
2.00000000000000E+0000 2.82448607935987E-0019
3.00000000000000E+0000 7.86974812262708E-0017
4.00000000000000E+0000 7.39441869845990E-0015
5.00000000000000E+0000 2.90985021530609E-0013
6.00000000000000E+0000 6.17501469624645E-0012
7.00000000000000E+0000 8.43767455081911E-0011
8.00000000000000E+0000 8.31773124213909E-0010
9.00000000000000E+0000 6.37567453464681E-0009
1.00000000000000E+0001 4.00099999988385E-0008
1.10000000000000E+0001 2.13281227462223E-0007
1.20000000000000E+0001 4.03586937610926E-0007
1.30000000000000E+0001 7.11606705941480E-0008
1.40000000000000E+0001 8.33336454193886E-0008
1.50000000000000E+0001 1.07542928787874E-0006
1.60000000000000E+0001 7.41617575745599E-0006
1.70000000000000E+0001 7.55488678400258E-0005
1.80000000000000E+0001 2.07697876763876E-0004
1.90000000000000E+0001 3.85618490701140E-0003
2.00000000000000E+0001 9.83042047999998E-0003
Если такое же возмущение вставить в программу с полиномом, корни которого заданы в разделе констант исходной программы ITERREKORN1680, –
const n1 = 40; b: array [1..n1] of extended = (1, 1.0001, 2, 2.0001, 3, 3.0001, 4, 4.0001, 5, 5.0001, 6, 6.0001, 7,
7.0001, 8, 8.0001, 9, 9.0001, 10, 10.0001, 11, 11.0001, 12, 12.0001, 13, 13.0001, 14, 14.0001, 15, 15.0001,
16, 16.0001, 17, 17.0001, 18, 18.0001, 19, 19.0001, 20, 20.0001);
затем с помощью подпрограммы func задать полином степени 560 с корнями, взаимно отделенными на 0,0001 и на 0,001, при возмущении коэффициентов из предыдущего кода,
function func (var x: extended): extended;
var i,i1,i2: integer;p,p1,p2:extended;
begin p: = 1; for i: = 1 to n1 do p: = p*(sqr(x)-sqr(b[i]));
p1: = 1; for i1: = 1 to n1 do for i2: = 1 to 3 do p1: = p1*(sqr(x)-sqr(b[i1]+i2*0.001));
p2: = 1; for i1: = 1 to n1 do for i2: = 1 to 3 do p2: = p2*(sqr(x)-sqr(b[i1]-i2*0.001));
func: = abs(p*p1*p2+1e-27*(sqr(sqr(sqr(sqr(x))))*x*x*x)+1e-26*(sqr(sqr(sqr(sqr(x))))*x*x)+
1e-25*(sqr(sqr(sqr(sqr(x))))*x)+1e-24*(sqr(sqr(sqr(sqr(x))))))+1e-22*((sqr(sqr(sqr(x))))*x*x*x -
1e-20*(sqr(sqr(sqr(x))))*x*x-1e-18*(sqr(sqr(sqr(x))))*x-1e-16*(sqr(sqr(sqr(x))))-1e-12*((sqr(sqr(x))))*x*x*x-
1e-8*((sqr(sqr(x))))*x*x-1e-4*((sqr(sqr(x))))*x-1*sqr(sqr(x))-1.4*sqr(x)*x-1.8*sqr(x)-2.2*x-2.6); end;
и с разделом инструкций
begin writeln ('PRIBLIJENIE'); writeln; x00: = -22; x11: = 22; eps0: = 0.00049/10; h: = eps0/43; eps00: = eps0;
ident(x00,x11,eps0, h); writeln; writeln ('TOCHN'); writeln; eps0: = eps0/10; h: = eps0/43;
for kk1: = 1 to kk do begin x00: = rex[kk1]-eps00; x11: = rex[kk1]+eps00;
ident(x00,x11,eps0, h); end; readln; end.
то программа найдет все 560 корней без потери значащих цифр их мантисс:
-2.00031000000000E+0001 3.28674871284977E-0003
-2.00030000000000E+0001 3.28642667889085E-0003
-2.00021000000000E+0001 3.28352971535904E-0003
-2.00020000000000E+0001 3.28320797959648E-0003
-2.00011000000000E+0001 3.28031369866020E-0003
-2.00010000000000E+0001 3.27999226083365E-0003
-2.00000000000000E+0001 3.27677951999999E-0003
-2.00001000000000E+0001 3.27710066015066E-0003
………………………………………………………….
-2.00310000000000E+0000 -1.53465946650750E-0019
-2.00300000000000E+0000 -1.53395508261575E-0019
-2.00200000000000E+0000 -1.52692470557641E-0019
-2.00210000000000E+0000 -1.52762664233116E-0019
-2.00110000000000E+0000 -1.52061827515068E-0019
-2.00100000000000E+0000 -1.51991878233121E-0019
-2.00010000000000E+0000 -1.51363433276626E-0019
-2.00000000000000E+0000 -1.51293728063987E-0019
………………………………………………………….
2.00000000000000E+0001 9.83042047999998E-0003
2.00001000000000E+0001 9.83131836319032E-0003
2.00010000000000E+0001 9.83940281061152E-0003
2.00011000000000E+0001 9.84030147140918E-0003
2.00020000000000E+0001 9.84839292015945E-0003
2.00021000000000E+0001 9.84929235920078E-0003
2.00030000000000E+0001 9.85739081500944E-0003
2.00031000000000E+0001 9.85829103293127E-0003
Можно предположить, что при использовании предложенного метода устойчивость вычисления вещественных корней полинома можно обеспечить существующими средствами компьютерного приближения коэффициентов.
Замечание 6. Однако само значение полинома в идентифицированных корнях остается возмущенным – вычисленным с низкой точностью. В целом это не ошибка, поскольку при возмущении коэффициентов идентифицируются корни другого (по сравнению с невозмущенным) полинома, и полученные значения корней совпали только в границах использованного формата числовых данных.
Границы применимости метода в случае комплексных корней полинома
В этом случае корни полинома при наличии малой взаимной отделенности идентифицируются существенно более длительно [9], чем в случае вещественных корней. С учетом длительности вычислений и с целью визуального контроля исходные значения вещественных и мнимых частей корней будут взаимно отделяться всего на 0,1. Исходная программа идентификации комплексных корней полинома с комплексными коэффициентами почти без изменений заимствуется из [9]. Там же приводится подробное описание метода, которое для краткости здесь не повторяется. Однако существенное изменение состоит в исключении операторов if abs(aaa-x)< = 1e-50 then goto 23; if abs(bbb-yk0)< = 1e-50 then goto 22. В приводимой ниже программе они отмечены комментарием //. В экспериментах эти операторы исключали некоторые корни с совпадающими вещественными или мнимыми частями. Кроме того, не используется отсечение приближений с большим значением модуля полинома (закомментировано в программе).
Для полинома степени n от комплексной переменной 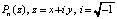 , после перехода к квадрату модуля по соотношению
, после перехода к квадрату модуля по соотношению
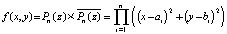 , (13)
, (13)
идентифицируются минимумы модуля функции двух вещественных переменных, которые соответствуют действительным и мнимым частям искомых комплексных корней. Соотношение (13) элементарно выводится из основной теоремы высшей алгебры, ai, bi – вещественная и мнимая части i-го корня полинома. Описанные для случая вещественных корней принципы по отдельности применяются к обеим переменным функции (13). Идентификацию корней реализует программа:
PROGRAM ITERKOMPKORN100;
{$APPTYPE CONSOLE} uses SysUtils;
const n00 = 1024; np1 = 20; type vect3 = array [1..np1] of extended;
const b: vect3 = (-0.1,-0.2,-0.3,-0.4,-0.5,-0.6,-0.7,-0.8,-0.9,-1,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1);
b1: vect3 = (0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,-0.1,-0.2,-0.3,-0.4,-0.5,-0.6,-0.7,-0.8,-0.9,-1);
type vect1 = array [1..4*n00] of extended; vect2 = array [1..4*n00] of longint;
var i,ii,j,k,kk,k1,r,ee,ee1,tty,nn0,mm: longint; c,a1,rex,imy: vect1; e,e3,e33: vect2;
aaa,x,x0,xk,xk0,xk1,hx,hy,min,eps1,eps11,eps12,eps13,z,z1,bbb,
y,y0,yk,yk0,yk1,ykk0,aak,bbk,hh,yz,yz1,x00,x11,y00,y11,eps0,h,eps00,eps: extended;
procedure sort(var nn0: longint; var c: vect1; var e: vect2);
type vecc = array[0..4*n00] of longint; var ab: integer; i,j,k,l,m,r,nm,p,n: longint; e1, e2: vecc;
begin p: = trunc(ln(nn0)/ln(2)); if p <> ln(nn0)/ln(2) then p : = p+1; n: = round(exp(p*ln(2)));
for l : = 1 to n do if l< = nn0 then e[l] : = l else ab: = 1; for r : = 1 to p do begin m : = round(exp(r*ln(2)));
nm: = n div m; for k : = 0 to nm-1 do begin for l : = 1 to m div 2 do begin
if (k * m + l > nn0) or (e[k * m + l]>nn0) then ab : = l else e1[l] : = e[k * m + l];
if (k * m + m div 2+ l > nn0) or (e[k * m + m div 2+ l]>nn0) then ab : = 1 else e2[l] : = e[k * m + m div 2 + l]
end; i : = 1; j : = 0; while i + j < = m do begin if i = m div 2 + 1 then ab : = -1; if j = m div 2 then ab : = 1;
if (k * m + i > nn0) or (e[k * m + i]>nn0) or (k * m + m div 2 + j > nn0-1) or (e[k * m + m div 2+ j]>nn0)
then ab: = 1; if (i < = m div 2) and (j < = m div 2 -1) and (k * m + i< = nn0) and (k * m + m div 2 + j < = nn0-1)
then if (e2[j + 1] > nn0) or (e1[i]> nn0) then ab : = 1 else begin if c[e2[j + 1]] - c[e1[i]] = 0 then ab : = 0;
if c[e2[j + 1]] - c[e1[i]]> 0 then ab : = 1; if c[e2[j + 1]] - c[e1[i]]< 0 then ab : = -1 end; if ab > = 0 then begin
e[k * m + i + j] : = e1[i]; i : = i + 1 end else begin e[k * m + i + j] : = e2[j + 1]; j : = j + 1 end end end end end;
procedure identif1(var eps,x00,x11,y00,y11,eps0,h,x,yk0:extended;
var rex,imy: vect1;var kk:longint;var mm:longint);
label 21,22,23;
function func (x,y:extended):extended;
var p,p0,p1:extended; i1,i2: integer;
begin p: = 1; for i1: = 1 to np1 do p: = p*(sqr(x-b[i1])+sqr(y-b1[i1]));
p1: = 1; for i1: = 1 to np1 do for i2: = 1 to 2 do p1: = p1*(sqr(x-(b[i1]+i2*1))+sqr(y-(b1[i1]+i2*1)));
p0: = 1; for i1: = 1 to np1 do for i2: = 1 to 2 do p0: = p0*(sqr(x-(b[i1]-i2*1))+sqr(y-(b1[i1]-i2*1)));
func: = abs(p*p1*p0); end;
procedure minx (var x,y,min:extended;var ee:integer);
begin min: = func(x,y); ee: = 0; for i: = 1 to mm do begin x: = xk0+i*hx;
if min > func(x,y) then begin min: = func(x,y);ee: = i end end end;
procedure miny (var x,y,min:extended;var ee1:integer);
begin min: = func(x,y); ee1: = 0; for i: = 1 to tty do begin y: = ykk0+i*hy;
if min > func(x,y) then begin min: = func(x,y);ee1: = i end end end;
procedure spuskx( var eps1, xk0,xk1,hx,y: extended);
begin while abs(eps1) > eps do begin x: = xk0; minx (x,y,min,ee); eps1: = eps1/1.2;
xk0: = xk0+ee*hx-eps1;xk1: = xk0+eps1;hx: = abs(2*eps1)/mm end end;
procedure spusky(var eps11,yk0,yk1,hy,x: extended);
begin while abs(eps11) > eps do begin ykk0: = yk0; y: = yk0; tty: = mm;
miny (x,y,min,ee1); eps11: = eps11/1.2; yk0: = yk0+ee1*hy-eps11; yk1: = yk0+eps11;
hy: = abs(2*eps11)/mm end end;
begin {aaa: = 1e62;bbb: = 1e62;} kk: = 0; x0: = x00; y0: = y00; nn0: = n00; hh: = nn0*h;
while x0 < = x11+hh do begin while y0 < = y11+hh do begin for r: = 1 to nn0 do
begin x: = x0+r*h; ykk0: = y0; y: = y0; tty: = n00; hy: = h; miny (x,y,min,ee1); a1[r]: = min end; sort( nn0, a1, e3);
k: = 1; while k< = nn0 do begin for r: = 1 to k-1 do if abs(e3[k]-e3[k-r]) < = eps0/h then goto 23; xk: = x0+e3[k]*h;
for r: = 1 to nn0 do begin y: = y0+r*h; a1[r]: = func(xk,y) end; sort(nn0, a1, e33); k1: = 1; while k1< = nn0 do begin
for r : = 1 to k1-1 do if abs(e33[k1]-e33[k1-r])< = eps0/h then goto 22; yk: = y0+e33[k1]*h; eps1: = eps0;
eps11: = eps0; xk0: = xk-eps1; xk1: = xk+eps1; hx: = abs(2*eps1)/mm; y: = yk; spuskx(eps1,xk0,xk1,hx,y);
yk0: = yk-eps11; yk1: = yk+eps11; hy: = abs(2*eps11)/mm; x: = xk0+ee*hx+eps1; spusky(eps11,yk0,yk1,hy,x);
eps12: = eps0/1.2; xk0: = x-eps12; xk1: = x+eps12; hx: = abs(2*eps12)/mm; y: = yk0+ee1*hy+eps11;
spuskx(eps12, xk0,xk1,hx,y); eps13: = eps0/1.2; yk0: = yk0+ee1*hy-eps13; yk1: = yk0+2*eps13;
hy: = abs(2*eps13)/mm; x: = xk0+ee*hx+eps12; spusky( eps13,yk0,yk1,hy,x);
if func(xk,yk) = 0 then begin x: = xk; yk0: = yk; goto 21 end;
for i: = 1 to 2 do begin z: = x+i*h; if func(x,yk0) > = func(z,yk0) then goto 23; end;
for i: = 1 to 2 do begin z1: = x-i*h; if func(x,yk0) > = func(z1,yk0) then goto 23; end;
for i: = 1 to 2 do begin yz: = yk0+i*h; if func(x,yk0) > = func(x,yz) then goto 22; end;
for i: = 1 to 2 do begin yz1: = yk0-i*h; if func(x,yk0) > = func(x,yz1) then goto 22; end;
//if abs(aaa-x)< = 1e-50 then goto 23; if abs(bbb-yk0)< = 1e-50 then goto 22;
21: kk: = kk+1; rex[kk]: = x; imy[kk]: = yk0;{if abs(func(x,yk0))< = e-1 then begin}
writeln (' ', x,' '); writeln (' ', yk0,' ',' ', func(x,yk0)); {end;} writeln; {aaa: = x; bbb: = yk0;}
22: k1: = k1+1 end;
23: k: = k+1 end; y0: = y0+hh end; x0: = x0+hh; y0: = y00 end; end;
begin
eps: = 1e-44; mm: = 4; x00: = -3.1; x11: = 3.1; y00: = -3.1; y11: = 3.1; eps0: = 0.049/2/3; h: = eps0/43/2; eps00: = eps0;
writeln (' ','PRIBLIJENIE',' '); writeln; identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); writeln;
writeln (' ', 'TOCHNOE',' '); writeln; for ii: = 1 to kk do begin x00: = rex[ii]- eps0;x11: = rex[ii]+ eps0;
y00: = imy[ii]- eps0; y11: = imy[ii]+ eps0; eps0: = eps00/10/2/3; h: = eps0/43/2;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); end; readln; end.
Вещественные части корней заданы массивом b, мнимые – массивом b1, так что вместо (x – ai)2 + (y –bi)2, где ai, bi – вещественная и мнимая части i-го корня полинома в (13), в программе задается sqr(x-b[i])+sqr(y-b1[i]). Квадрат модуля полинома p степени np1 (np1 = 20) определяется в подпрограмме func (x,y). Затем в этой же подпрограмме на основе корней полинома p циклически формируются квадраты модулей еще двух полиномов: p1 и p0. Первый – путем добавления к вещественной и мнимой части каждого корня полинома p значения i2*1, второй – путем добавления к вещественной и мнимой части каждого корня полинома p значения -i2*1. В данном примере оба вложенных цикла состоят из двух шагов. Квадраты модулей всех трех полиномов перемножаются. В результате образуется квадрат модуля полинома func: = abs(p*p1*p0); степень такого полинома равна 100: np1+ 2*np1+2*np1 = 100. Таким образом, программа должна идентифицировать 100 комплексных корней полинома 100-й степени. Границы области и радиусы локализации задаются в разделе инструкций – для приближения ('PRIBLIJENIE'): x00: = -3.1; x11: = 3.1; y00: = -3.1; y11: = 3.1; eps0: = 0.049/2/3; h: = eps0/43/2; eps00: = eps0; затем для уточнения – ('TOCHNOE'): for ii: = 1 to kk do begin x00: = rex[ii]- eps0;x11: = rex[ii]+ eps0; y00: = imy[ii]- eps0;y11: = imy[ii]+ eps0; eps0: = eps00/10/2/3; h: = eps0/43/2. Относительно точные границы прямоугольной области всех корней можно найти, как и в вещественном случае, путем быстрого решения задачи со сравнительно большим радиусом локализации. Точнее, можно большой радиус взять для приближения, а меньший в расширенных границах – для уточнения. Так, раздел инструкций
begin eps: = 1e-44; mm: = 4; x00: = -30; x11: = 30; y00: = -30; y11: = 30; eps0: = 0.49; h: = eps0/43; eps00: = eps0;
writeln; writeln (' ','PRIBLIJENIE',' '); writeln; identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
writeln; writeln (' ', 'TOCHNOE',' '); writeln; for ii: = 1 to kk do begin
x00: = rex[ii]- 10*eps0; x11: = rex[ii]+ 10*eps0; y00: = imy[ii]- 10*eps0; y11: = imy[ii]+ 10*eps0;
eps0: = eps00/10/2; h: = eps0/43; identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); end; readln; end
задает параметры, с которыми программа в границах квадрата 60×60 за 4 мин выдает наименьшие и наибольшие значения вещественной части корней -3.0, + 3.0, и, аналогично, мнимой части: -3.0, + 3.0. Остается с небольшим запасом взять границы области из представленной выше программы ITERKOMPKORN100.
Замечание 7. Добавления к вещественной и мнимой части каждого корня полинома p значений i2*1 и -i2*1, а не меньших величин, как это было в вещественном случае, помимо наглядности обусловлено тем, что добавление десятичных долей повлекло бы дублирование корней. Добавление же сотых и менее долей привело бы к необходимости на порядок и более уменьшить радиус локализации. Это принципиально замедлило бы программу и сделало бы невозможным экспериментальное изучение границ роста степеней полинома.
Результат работы программы ITERKOMPKORN100 (в левой колонке парами – вещественная и мнимая часть корня, в правой – значение в нем полинома):
-3.00000000000000E+0000
-1.00000000000000E+0000 0.00000000000000E+0000
-2.90000000000000E+0000
-1.10000000000000E+0000 0.00000000000000E+0000
-2.70000000000000E+0000
-1.30000000000000E+0000 0.00000000000000E+0000
-2.80000000000000E+0000
-1.20000000000000E+0000 0.00000000000000E+0000
………………………………………………………………
0.00000000000000E+0000
-2.00000000000000E+0000 0.00000000000000E+0000
………………………………………………………………
2.00000000000000E+0000
0.00000000000000E+0000 0.00000000000000E+0000
………………………………………………………………
0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
……………………………………………………
2.70000000000000E+0000
1.30000000000000E+0000 0.00000000000000E+0000
2.60000000000000E+0000
1.40000000000000E+0000 0.00000000000000E+0000
2.80000000000000E+0000
1.20000000000000E+0000 0.00000000000000E+0000
2.90000000000000E+0000
1.10000000000000E+0000 0.00000000000000E+0000
3.00000000000000E+0000
1.00000000000000E+0000 0.00000000000000E+0000
Найдены 100 различных комплексных корней полинома степени 100 с комплексными коэффициентами без потери значащих цифр мантисс в формате представления данных. Программа выполняется 1 ч 55 мин.
Замечание 8. Можно изменить параметры программы так, что она будет выполняться за 20 мин – для приближения: eps0: = 0.049/2; h: = eps0/43/2; для уточнения: x00: = rex[ii]-eps0; x11: = rex[ii]+eps0; y00: = imy[ii]-eps0; y11: = imy[ii]+eps0; eps0: = eps00/10/2; h: = eps0/43/2; В этом случае корни придется искать не только в результатах уточнения ('TOCHNOE'), но и в результатах приближения ('PRIBLIJENIE'). Процедура уточнения может пропустить некоторые корни, хотя они будут идентифицированы в результатах процедуры приближения.
Последовательное добавление именно ±1 при циклическом формировании степени полинома, как отмечалось, выбрано для визуальной проверки результатов. Иначе можно было бы задать любой набор корней с радиусом локализации меньшим половины минимального ненулевого расстояния между различными вещественными и различными мнимыми частями корней [9]. В программе ITERKOMPKORN100 радиус дополнительно уменьшен на случай полиномов с экспериментально высокими степенями. Можно было бы полностью исключить вывод неточных приближений по условию, которое закомментировано в программе: if abs(func(x,yk0))< = e-10 then begin writeln (' ', x,' '); writeln (' ', yk0,' ',' ', func(x,yk0)); end.
Результаты программы проверялись следующим образом. Выходной файл копировался с консоли и сохранялся как текстовый файл Word, где поиск требуемого корня осуществлялся опцией «Найти» по маске вещественной части. Выбирались последовательные пары вещественной и мнимой части каждого корня, заданные в массивах b, b1 начиная с пары -0.1, 0.1. В разделе файла TOCHNOE выполнялся поиск вещественной части корня -0.1. Среди найденных значений фиксировались те значения корней, у которых мнимая часть равна 0.1. При этом их вещественная и мнимая части в формате с плавающей точкой отображаются с множителем 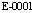 , а сами они представлены как
, а сами они представлены как 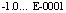 и
и 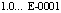 . Если идентифицировался правильный результат, то на основании алгоритма генерации корней полинома совершенно аналогично выполнялся поиск пары
. Если идентифицировался правильный результат, то на основании алгоритма генерации корней полинома совершенно аналогично выполнялся поиск пары 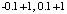 , то есть вещественной части корня 0.9 и мнимой части 1.1 в формате
, то есть вещественной части корня 0.9 и мнимой части 1.1 в формате 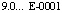 и
и 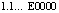 . После идентификации правильного результата выполнялся поиск следующей пары
. После идентификации правильного результата выполнялся поиск следующей пары 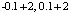 , то есть 1.9 и 2.1. Если был найден верный результат, то выполнялся переход к поиску
, то есть 1.9 и 2.1. Если был найден верный результат, то выполнялся переход к поиску 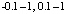 , то есть -1.1 и -0.9. Затем, аналогично,
, то есть -1.1 и -0.9. Затем, аналогично, 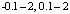 , то есть -2.1 и -1.9. В случае достоверности результата совершенно аналогично проверялась следующая пара -0.2, 0.2 и ее алгоритмические преобразования
, то есть -2.1 и -1.9. В случае достоверности результата совершенно аналогично проверялась следующая пара -0.2, 0.2 и ее алгоритмические преобразования 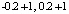 и
и 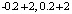 , затем
, затем 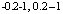 и
и 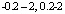 . Проверка продолжалась до исчерпания элементов массивов b, b1. Были найдены 100 различных корней полинома без потери значащих цифр мантисс в формате данных extended. При начальных проверках некоторые корни оказывались только в файле приближений. Тогда уменьшался радиус локализации процедуры уточнения, программа перезапускалась, и так – до окончательных значений параметров, при которых в файле уточнений оказывались все правильные результаты.
. Проверка продолжалась до исчерпания элементов массивов b, b1. Были найдены 100 различных корней полинома без потери значащих цифр мантисс в формате данных extended. При начальных проверках некоторые корни оказывались только в файле приближений. Тогда уменьшался радиус локализации процедуры уточнения, программа перезапускалась, и так – до окончательных значений параметров, при которых в файле уточнений оказывались все правильные результаты.
Если попытаться увеличить степень полинома, сделав число шагов вложенных циклов равным 5, то подпрограмма func примет вид
function func (x,y:extended):extended;
var p, p0, p1: extended; i1,i2: integer;
begin p: = 1; for i1: = 1 to np1 do p: = p*(sqr(x-b[i1])+sqr(y-b1[i1]));
p1: = 1; for i1: = 1 to np1 do for i2: = 1 to 5 do p1: = p1*(sqr(x-(b[i1]+i2*1))+sqr(y-(b1[i1]+i2*1)));
p0: = 1; for i1: = 1 to np1 do for i2: = 1 to 5 do p0: = p0*(sqr(x-(b[i1]-i2*1))+sqr(y-(b1[i1]-i2*1)));
func: = abs(p*p1*p0); end;
Поскольку теперь к исходным значениям вещественной и мнимой части корней будет добавляться и вычитаться единица не два, а пять раз, то изменятся границы области корней. Это изменение определяется в разделе инструкций:
begin eps: = 1e-44; mm: = 4; x00: = -6.5; x11: = 6.5; y00: = -6.5; y11: = 6.5;
eps0: = 0.049/2/3; h: = eps0/43/2;eps00: = eps0; writeln; writeln ('PRIBLIJENIE'); writeln ;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);writeln; writeln ('TOCHNOE'); writeln;
for ii: = 1 to kk do begin x00: = rex[ii]-eps0; x11: = rex[ii]+eps0; y00: = imy[ii]-eps0; y11: = imy[ii]+eps0;
eps0: = eps00/10/2/3; h: = eps0/43/2; identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); end;
readln; end.
Иных изменений в программу ITERKOMPKORN100 не вносилось. Результат ее работы:
-6.00000000000000E+0000
-4.00000000000000E+0000 0.00000000000000E+0000
-5.90000000000000E+0000
-4.10000000000000E+0000 0.00000000000000E+0000
-5.70000000000000E+0000
-4.30000000000000E+0000 0.00000000000000E+0000
-5.80000000000000E+0000
-4.20000000000000E+0000 0.00000000000000E+0000
………………………………………………………………
-4.90000000000000E+0000
-3.10000000000000E+0000 0.00000000000000E+0000
-5.00000000000000E+0000
-3.00000000000000E+0000 0.00000000000000E+0000
-4.90000000000000E+0000
-5.10000000000000E+0000 0.00000000000000E+0000
……………………………………………………………….
0.00000000000000E+0000
-2.00000000000000E+0000 0.00000000000000E+0000
……………………………………………………………….
0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
……………………………………………………………….
-2.00000000000000E+0000
0.00000000000000E+0000 0.00000000000000E+0000
……………………………………………………………….
2.00000000000000E+0000
0.00000000000000E+0000 0.00000000000000E+0000
………………………………………………………………
5.70000000000000E+0000
4.30000000000000E+0000 0.00000000000000E+0000
5.80000000000000E+0000
4.20000000000000E+0000 0.00000000000000E+0000
5.90000000000000E+0000
4.10000000000000E+0000 0.00000000000000E+0000
6.00000000000000E+0000
4.00000000000000E+0000 0.00000000000000E+0000
Программа идентифицировала 220 комплексных корней полинома степени 220 с комплексными коэффициентами. Однако по сравнению с исходной программой для полинома степени 100 она проявляет два существенных недостатка. Первый – некоторые из корней, идентифицированных в приближении, программа может пропустить при уточнении. Хотя все они не изменят значащих цифр мантисс в формате вывода. Второй – программа выполняется свыше 12 ч. Ее можно ускорить до 5,5 ч за счет увеличения начального радиуса локализации, и при этом сохранится качество идентификации корней, однако не будет гарантии, что некоторые корни не окажутся пропущенными.
По причине длительности работы программы на этом можно было бы завершить эксперименты по увеличению степени полинома, но тема требует продолжения, которое целесообразно изложить после попытки дополнительно удвоить степень полинома. Для искомого увеличения степени полинома подпрограмма его генерации принимается в виде
function func (x,y:extended):extended;
var p,p1,p0: extended; i1,i2: integer;
begin p: = 1; for i1: = 1 to np1 do p: = p*(sqr(x-b[i1])+sqr(y-b1[i1]));
p1: = 1; for i1: = 1 to np1 do for i2: = 1 to 10 do p1: = p1*(sqr(x-(b[i1]+i2*1))+sqr(y-(b1[i1]+i2*1)));
p0: = 1; for i1: = 1 to np1 do for i2: = 1 to 10 do p0: = p0*(sqr(x-(b[i1]-i2*1))+sqr(y-(b1[i1]-i2*1)));
func: = abs(p*p1*p0); end;
Генерируется полином степени 420. Раздел инструкций принят в виде
вegin eps: = 1e-44; mm: = 4; x00: = -12; x11: = 12; y00: = -12; y11: = 12; eps0: = 0.049/2; h: = eps0/43/2; eps00: = eps0;
writeln; writeln (' ','PRIBLIJENIE',' '); writeln; identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
writeln; writeln (' ', 'TOCHNOE',' '); writeln; for ii: = 1 to kk do begin
x00: = rex[ii]-eps0; x11: = rex[ii]+eps0; y00: = imy[ii]-eps0; y11: = imy[ii]+eps0; eps0: = eps00/10/2/3;
h: = eps0/43/2; identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); end; readln; end.
Начальный радиус локализации увеличен до eps0: = 0.049/2; (иначе программа выполнялась бы неприемлемо долго). Результат работы программы:
-1.10000000000000E+0001
-9.00000000000000E+0000 0.00000000000000E+0000
-1.09000000000000E+0001
-9.10000000000000E+0000 0.00000000000000E+0000
-1.04000000000000E+0001
-9.60000000000000E+0000 0.00000000000000E+0000
-1.06000000000000E+0001
-9.40000000000000E+0000 0.00000000000000E+0000
-1.07000000000000E+0001
-9.30000000000000E+0000 0.00000000000000E+0000
-1.08000000000000E+0001
-9.20000000000000E+0000 0.00000000000000E+0000
………………………………………………………………
-2.00000000000000E+0000
-9.79570305531453E-0045 1.75265537401960E+0585
………………………………………………………………
9.79570305531453E-0045
2.00000000000000E+0000 1.75265537401960E+0585
………………………………………………………………
9.79570305531453E-0045
-2.00000000000000E+0000 1.75265537401960E+0585
………………………………………………………………
2.00000000000000E+0000
0.00000000000000E+0000 0.00000000000000E+0000
………………………………………………………………
1.07000000000000E+0001
9.30000000000000E+0000 0.00000000000000E+0000
1.05000000000000E+0001
9.50000000000000E+0000 0.00000000000000E+0000
1.06000000000000E+0001
9.40000000000000E+0000 0.00000000000000E+0000
1.08000000000000E+0001
9.20000000000000E+0000 0.00000000000000E+0000
1.09000000000000E+0001
9.10000000000000E+0000 0.00000000000000E+0000
1.10000000000000E+0001
9.00000000000000E+0000 0.00000000000000E+0000
Некоторые из корней, идентифицированных в приближении, программа пропустила при уточнении. Все найденные корни не содержат изменения значащих цифр мантисс, за исключением трех корней, представленных в данной распечатке. Программа выполняется 12 ч 30 мин. Проверка выходных значений производилась выборочно, так что нельзя утверждать, что найдены все без исключения 420 комплексных корней полинома степени 420.
О снижении временной сложности на основе распараллеливания
Алгоритм идентификации корней полинома можно разделить на взаимно независимые части, которые при реализации в параллельной вычислительной системе не потребуют обмена. Пусть, например, рассматривается программа для полинома степени 220 с границами области x00: = -6.5; x11: = 6.5; y00: = -6.5; y11: = 6.5; Эта область разделяется, в частности, на следующие подобласти:
x00: = -6.5; x11: = -5.0; y00: = -6.5; y11: = 6.5; x00: = -5.5; x11: = -4.0; y00: = -6.5; y11: = 6.5;
x00: = -4.5; x11: = -3.0; y00: = -6.5; y11: = 6.5; x00: = -3.5; x11: = -2.0; y00: = -6.5; y11: = 6.5;
x00: = -2.5; x11: = -1.0; y00: = -6.5; y11: = 6.5; x00: = -1.5; x11: = 0.0; y00: = -6.5; y11: = 6.5;
x00: = -0.5; x11: = 1.0; y00: = -6.5; y11: = 6.5; x00: = 0.5; x11: = 2.0; y00: = -6.5; y11: = 6.5;
x00: = 1.5; x11: = 3.0; y00: = -6.5; y11: = 6.5; x00: = 2.5; x11: = 4.0; y00: = -6.5; y11: = 6.5;
x00: = 3.5; x11: = 5.0; y00: = -6.5; y11: = 6.5; x00: = 4.5; x11: = 6.0; y00: = -6.5; y11: = 6.5;
x00: = 5.5; x11: = 6.5; y00: = -6.5; y11: = 6.5;
Границы мнимых частей разделять без изменения структуры программы нельзя. В каждой из таких подобластей программа без изменений выполняется за 1,5 ч. Последовательно проходя каждую подобласть, программа получит все искомые значения корней полинома степени 220. Такое восстановление результатов работы программы было практически апробировано, когда после 11 ч работы всплеск напряжения вызвал перезагрузку компьютера с потерей данных. Переход от подобласти к смежной с ней не использует каких-либо предшествующих значений данных. Поэтому разделенная по подобластям программа могла бы быть реализованной на 13 параллельно работающих компьютерах без обмена данными за 1,5 ч. Условно можно полагать, что аналогичное ускорение достигалось бы в параллельной вычислительной системе на 13 процессорах. Деление на подобласти можно продолжить, сократив границы вещественных частей корней, например, вдвое. Соответственно на 26 процессорах время решения задачи сократилось бы до 0,75 ч. Продолжая процесс деления на подобласти, можно решить задачу за 0,325 часа на 52 процессорах, менее чем за 3 мин – на 208 процессорах и т.д. При этом не требуется межпроцессорный обмен. Если же допускать возможность обмена, то на подобласти делятся, помимо того, границы мнимых частей корней. В этом случае с учетом обмена меняется структура программы, но в потенциале возможно дополнительное ускорение. Временная сложность максимально параллельной формы алгоритма, лежащего в основе программы, достигает оценки 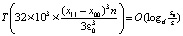 . Эта оценка и ее разновидности в зависимости от структуры алгоритма и сортировки, положенной в его основу, подробно выводятся в [9]. Правую часть оценки можно трактовать как O(1).
. Эта оценка и ее разновидности в зависимости от структуры алгоритма и сортировки, положенной в его основу, подробно выводятся в [9]. Правую часть оценки можно трактовать как O(1).
Представленная схема распараллеливания без обмена переносится на описанный ранее поиск области корней полинома в прямоугольнике больших размеров.
О восстановлении пропущенных корней полинома
Если нет уверенности, что найдены все корни полинома, формально возможен следующий подход. По найденным корням восстанавливаются коэффициенты полинома. Предпочтительно пользоваться алгоритмом из [7]: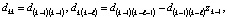
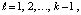
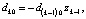 где zk – корни полинома,
где zk – корни полинома, 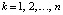 . При k = n получатся искомые коэффициенты:
. При k = n получатся искомые коэффициенты: 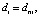
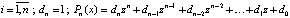 . Затем выполняется деление исходного полинома на только что сформированный полином из найденных корней. Полином в частном будет полиномом меньшей степени, чем в делимом. У него можно найти корни по изложенной ранее схеме, применив необходимое уменьшение радиусов локализации.
. Затем выполняется деление исходного полинома на только что сформированный полином из найденных корней. Полином в частном будет полиномом меньшей степени, чем в делимом. У него можно найти корни по изложенной ранее схеме, применив необходимое уменьшение радиусов локализации.
Более доступна следующая возможность. Из (13) по идентифицированным корням восстанавливается квадрат модуля полинома, корнями которого они являются. Составляется дробь, числителем которой будет квадрат модуля исходного полинома, а знаменателем – только что составленный квадрат модуля полинома из найденных корней. Теперь недостающие корни можно искать без изменения предложенной программы, в которой подпрограмма func примет вид (np0 – число предварительно идентифицированных корней):
function func (x,y:extended):extended;
var p,p0: extended; i1: integer;
begin p: = 1; for i1: = 1 to np1 do p: = p*(sqr(x-b[i1])+sqr(y-b1[i1])); p0: = 1; for i1: = 1 to np0
do p0: = p0*(sqr(x-b[i1])+sqr(y-b1[i1])); if p0<>0 then func: = abs(p/p0) else func: = abs(p); end;
Так, в случае np0 = 10, с корнями из раздела констант исходной программы ITERKOMPKORN100
const b: vect3 = (-0.1,-0.2,-0.3,-0.4,-0.5,-0.6,-0.7,-0.8,-0.9,-1,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1);
b1: vect3 = (0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,-0.1,-0.2,-0.3,-0.4,-0.5,-0.6,-0.7,-0.8,-0.9,-1); (14)
программа выдаст корни только с положительной вещественной частью:
1.00000000000000E-0001
-1.00000000000000E-0001 0.00000000000000E+0000
2.00000000000000E-0001
-2.00000000000000E-0001 0.00000000000000E+0000
………………………………………………………………
9.00000000000000E-0001
-9.00000000000000E-0001 0.00000000000000E+0000
1.00000000000000E+0000
-1.00000000000000E+0000 0.00000000000000E+0000
В случае изменения цикла в виде p0: = 1; for i1: = np0+1 to np1 do p0: = p0*(sqr(x-b[i1])+ sqr(y-b1[i1])); программа выдаст корни из того же набора, но только с отрицательной вещественной частью. Сомножители из (13) с одинаковыми корнями полиномов числителя и знаменателя ведут себя так, как если бы они алгебраически сокращались. Однако этот процесс требует значений параметров, приводимых в разделе инструкций:
begin eps: = 1e-44; mm: = 4; x00: = -1.2; x11: = 1.2; y00: = -1.2; y11: = 1.2; eps0: = 0.049/2/2; h: = eps0/43/2;
eps00: = eps0; identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); for ii: = 1 to kk do
begin x00: = rex[ii]-eps0; x11: = rex[ii]+eps0; y00: = imy[ii]-eps0;y11: = imy[ii]+eps0; eps0: = eps00/10/2/2;
h: = eps0/43/2; identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); end; readln; end. (15)
Без специального исследования неясно, будет ли работать этот прием в случае полиномов предельно высоких степеней и какие значения параметров при этом потребуются. Можно добавить, что оба полинома дроби могут синхронно вычисляться на параллельно работающих процессорах. Кроме того для их вычисления могут использоваться схемы распараллеливания вычисления полиномов.
О влиянии возмущения коэффициентов полинома на идентификацию комплексных корней
Согласно экспериментам, набор которых не претендует на полноту, возмущение коэффициентов полинома с комплексными корнями влияет на точность идентификации корней ненамного более, чем в случае полинома с вещественными корнями. Так, если взять рассматриваемую программу ITERKOMPKORN100 с набором комплексных корней (14), а квадрат модуля полинома возмутить путем его сложения с тем же полиномом, который использовался для возмущения в случае вещественных корней, подпрограмма func примет вид
function func (x,y:extended):extended;
var p:extended; i1: integer;
begin p: = 1; for i1: = 1 to np1 do p: = p*(sqr(x-b[i1])+sqr(y-b1[i1]));
func: = abs(p+1e-27*(sqr(sqr(sqr(sqr(x))))*x*x*x)+1e-26*(sqr(sqr(sqr(sqr(x))))*x*x)+
1e-25*(sqr(sqr(sqr(sqr(x))))*x)+1e-24*(sqr(sqr(sqr(sqr(x))))))+1e-22*((sqr(sqr(sqr(x))))*x*x*x -
1e-20*(sqr(sqr(sqr(x))))*x*x-1e-18*(sqr(sqr(sqr(x))))*x-1e-16*(sqr(sqr(sqr(x))))-1e-12*((sqr(sqr(x))))*x*x*x-
1e-8*((sqr(sqr(x))))*x*x-1e-4*((sqr(sqr(x))))*x-1*sqr(sqr(x))-1.4*sqr(x)*x-1.8*sqr(x)-2.2*x-2.6); end;
С последним разделом инструкций (15) получится следующий результат работы программы:
-1.00000000000000E+0000
1.00000000000000E+0000 -2.79081000999900E-0022
-9.00000000000000E-0001
9.00000000000000E-0001 -2.02555164542026E-0022
-8.00000000000000E-0001
8.00000000000000E-0001 -1.77040596623799E-0022
………………………………………………………………
9.00000000000000E-0001
-9.00000000000000E-0001 -7.39891230590379E-0022
8.00000000000000E-0001
-8.00000000000000E-0001 -6.55222748617176E-0022
1.00000000000000E+0000
-1.00000000000000E+0000 -7.98899001000100E-0022
Все корни полинома 20-й степени при возмущении всех коэффициентов, кроме старшего единичного коэффициента, идентифицированы без потери значащих цифр мантиссы.
Замечание 9. То, что значения полинома в найденных корнях определены лишь как приближения к точным нулевым значениям, не ошибка, потому что найдены корни другого полинома с измененными коэффициентами. Множество всех корней полинома взаимно однозначно соответствует множеству его коэффициентов. Найденные корни совпадают с корнями полинома с невозмущенными коэффициентами только в данном формате вывода данных. За пределами формата младшие разряды уже не совпадали бы с разрядами корней невозмущенного полинома. Так, даже в данном формате значение
-1.00000000000000E+0000
1.00000000000000E+0000 -2.79081000999900E-0022
заимствовано из файла приближений, – в файле уточнений оно имело вид
-9.99999999999999E-0002
1.00000000000000E-0001 -2.39669999901001E-0022
Устойчивость к возмущению коэффициентов проявляется и в примере, аналог которого часто приводят [13] в качестве примера ожидаемой неустойчивости. Именно, будут рассматриваться полиномы в левых частях уравнений
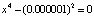 ,
, 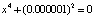 . (16)
. (16)
Справедливо утверждается, что ошибка в задании свободного члена «всего» на 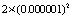 превратит вещественные корни в комплексные, и наоборот. В (16) задается подобный свободный член
превратит вещественные корни в комплексные, и наоборот. В (16) задается подобный свободный член 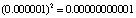 . Однако программа ошибки не совершает, выдавая для первого уравнения два комплексно сопряженных мнимых корня и два вещественных корня противоположных знаков с одинаковым модулем вещественных и мнимых частей 0.001.
. Однако программа ошибки не совершает, выдавая для первого уравнения два комплексно сопряженных мнимых корня и два вещественных корня противоположных знаков с одинаковым модулем вещественных и мнимых частей 0.001.
Для второго уравнения программа выдает четыре попарно комплексно-сопряженных корня с одинаковым модулем вещественных и мнимых частей без потери значащих цифр.
Чтобы это показать, требуются изменения в программе, которые включают подпрограммы комплексного сложения и умножения, подпрограмму схемы Горнера для вычисления полиномов с комплексными коэффициентами. Подпрограмма func в этом случае задает корень квадратный из суммы квадратов вещественной и мнимой части значения полинома. Ниже приводится измененная таким образом часть предыдущей программы:
PROGRAM ITERKOMPKORDVOICHNCOEF;
{$APPTYPE CONSOLE} uses SysUtils;
const n00 = 1024; n1 = 4{20}; type vect3 = array [0..n1] of extended; type vect1 = array [1..4*n00] of extended;
vect2 = array [1..4*n00] of longint; var i,ii,j,k,kk,k1,r,ee,ee1,tty,nn0,mm: longint; c,a1,rex,imy: vect1;
e,e3,e33: vect2; aaa,x,x0,xk,xk0,xk1,hx,hy,min,eps1,eps11,eps12,eps13,z,z1,bbb,
y,y0,yk,yk0,yk1,ykk0,aak,bbk,hh,yz,yz1,x00,x11,y00,y11,eps0,h,eps00,eps: extended;
a,b,a11,b11, ca,cb: extended; bdv, bmv: vect3; p1,p2,d1,d2: extended; pp1,pp2,d3,d4: extended;
procedure sort(var nn0:longint; var c: vect1; var e: vect2);
type vecc = array[0..4*n00] of longint; var ab: integer; i,j,k,l,m,r,nm,p,n: longint; e1, e2: vecc;
begin
…{полное повторение подпрограммы сортировки}
end;
procedure identif1(var eps,x00,x11,y00,y11,eps0,h,x,yk0:extended;
var rex,imy: vect1;var kk:longint;var mm:longint);
label 21,22,23;
{процедура комплексного умножения}
procedure um(var a,b,a11,b11: extended; var ca,cb: extended);
begin ca: = a*a11-b*b11; cb: = a*b11+b*a11 end;
{процедура комплексного сложения}
procedure sum(var a,b,a11,b11: extended; var ca,cb: extended);
begin ca: = a+a11; cb: = b+b11 end;
function func (var x,y: extended; var bdv, bmv: vect3): extended;
var i1: integer; p1,p2,pp1,pp2,d1,d2,d3,d4:extended;
begin
{задание коэффициентов полинома в порядке от старших к младшим в комплексной форме:
Re; Im в порядке соответствия индексов}
bdv[n1]: = 1;bdv[n1-1]: = 0;bdv[n1-2]: = 0;bdv[n1-3]: = 0;bdv[n1-n1]: = -1*{*+1}sqr(0.000001);
bmv[n1]: = 0; bmv[n1-1]: = 0;bmv[n1-2]: = 0;bmv[n1-3]: = 0;bmv[n1-n1]: = 0;
{аналог схемы Горнера}
p1: = bdv[n1]; p2: = bmv[n1]; for i1: = 1 to n1 do begin um(p1,p2,x,y,d1,d2);
pp1: = bdv[n1-i1];pp2: = bmv[n1-i1]; sum(pp1,pp2,d1,d2,d3,d4); p1: = d3; p2: = d4; end;
{модуль полинома} func: = sqrt(sqr(p1)+sqr(p2)); end;
{полное повторение соответственной части предыдущей программы}
………………………………………………………………………………
{расширение формата вывода} writeln (' ', x:2:30,' ');
writeln (' ', yk0:2:30,' ',' ', func(x,yk0,bdv, bmv):2:30); {end;} writeln; {aaa: = x; bbb: = yk0;}
22: k1: = k1+1 end;
23: k: = k+1 end; y0: = y0+hh end; x0: = x0+hh; y0: = y00 end; end;
{раздел инструкций с изменением границ области корней}
вegin eps: = 1e-44; mm: = 4; x00: = -0.2; x11: = 0.2; y00: = -0.2; y11: = 0.2; eps0: = 0.049/2/3; h: = eps0/43/2;
eps00: = eps0; writeln; writeln (' ','PRIBLIJENIE',' '); writeln;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); writeln; writeln (' ', 'TOCHNOE',' '); writeln;
for ii: = 1 to kk do begin x00: = rex[ii]-eps0; x11: = rex[ii]+eps0; y00: = imy[ii]-eps0; y11: = imy[ii]+eps0;
eps0: = eps00/10/2/3; h: = eps0/43/2; identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); end;
readln; end.
Результат работы программы для первого уравнения (16):
-0.001000000000000000000000000000
-0.000000000000000000000000000000 0.000000000000000000000000000000
0.001000000000000000000000000000
-0.000000000000000000000000000000 0.000000000000000000000000000000
-0.000000000000000000000000000000
0.001000000000000000000000000000 0.000000000000000000000000000000
-0.000000000000000000000000000000
-0.001000000000000000000000000000 0.000000000000000000000000000000
Результат работы программы для второго уравнения (16):
-0.000707106781186550000000000000
-0.000707106781186550000000000000 0.000000000000000000000000000000
-0.000707106781186550000000000000
0.000707106781186550000000000000 0.000000000000000000000000000000
0.000707106781186550000000000000
-0.000707106781186550000000000000 0.000000000000000000000000000000
0.000707106781186550000000000000
0.000707106781186550000000000000 0.000000000000000000000000000000
Необходимо принять во внимание, что в общем случае имеет место непрерывная зависимость корней полинома от его коэффициентов [14]. Средства современной вычислительной техники таковы, что позволяют реализовать эту непрерывную зависимость на практике путем вычисления коэффициентов с достаточно малой погрешностью.
Об идентификации корней полинома с явно заданными комплексными коэффициентами
Пусть полином задан в виде (9), где dn = 1, коэффициенты и корни, вообще говоря, комплексные. Тогда имеют место оценки Маклорена границ области корней [4, 13]: если 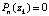 , то
, то
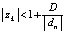 ,
, 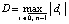 , (17)
, (17)
кроме того,
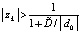 ,
, 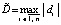 . (18)
. (18)
В последней модификации программы, ITERKOMPKORDVOICHNCOEF, любые коэффициенты полинома, в том числе комплексные, задаются в явной форме. Например, фрагмент
bdv[n1]: = 1;bdv[n1-1]: = 3.7; bdv[n1-2]: = 0; bdv[n1-3]: = 2.1;bdv[n1-4]: = 1; bdv[n1-5]: = -1; bdv[n1-6]: = 1.9;
bmv[n1]: = 0; bmv[n1-1]: = -1.5; bmv[n1-2]: = 1; bmv[n1-3]: = 0;bmv[n1-4]: = 1.04; bmv[n1-5]: = -1.04;bmv[n1-6]: = -2.04;
задает коэффициенты следующего полинома 6-й степени (в этом случае в разделе констант следует положить n1 = 6):
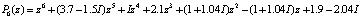 . (19)
. (19)
С применением (17) к (19) сначала корни ищутся в границах x00: = -5; x11: = 5; y00: = -5; y11: = 5; с увеличенным радиусом локализации приближения eps0: = 0.49; h: = eps0/43/2; для уточнения берется радиус eps0: = eps00/10; h: = eps0/43/2; Программа выдает неточные приближения корней, по которым видно, что не равные друг другу вещественные и мнимые части корней отделены друг от друга не менее чем на 0.07 и что границы вещественной и мнимой части искомых корней можно задать следующими параметрами раздела инструкций:
eps: = 1e-44; mm: = 4; eps: = 1e-44; x00: = -3.9; x11: = 0.8; y00: = -0.8; y11: = 1.7; eps0: = 0.049/2/3;
h: = eps0/43/2;eps00: = eps0; writeln; writeln (' ','PRIBLIJENIE',' ');writeln ;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); writeln; writeln (' ', 'TOCHNOE',' '); writeln;
for ii: = 1 to kk do begin x00: = rex[ii]-eps0; x11: = rex[ii]+eps0; y00: = imy[ii]-eps0;y11: = imy[ii]+eps0;
eps0: = eps00/10/2/3; h: = eps0/43/2; identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); end;
readln; end.
Результат работы программы для полинома (19):
-3.885209853120340830000000000000
1.655183190703654950000000000000 0.000000000000000120000000000000
-0.872107396021157320000000000000
-0.090421193411493330000000000000 0.000000000000000000000000000000
-0.188134868546058860000000000000
-0.788488795098142880000000000000 0.000000000000000000000000000000
-0.111539596247773910000000000000
1.117173994400358400000000000000 0.000000000000000000000000000000
0.640160549309086680000000000000
-0.784905169635334860000000000000 0.000000000000000000000000000000
0.716831164626244240000000000000
0.391457973040957710000000000000 0.000000000000000000000000000000
Найдены шесть комплексных корней, обращающих в ноль полином (19).
Замечание 10. В первом из корней полином обратился в ноль не точно, а в приближении – с ошибочными цифрами в 16-м и 17-м знаках мантиссы. Устранить эту неточность не удается. Причина – выполнение схемы Горнера с комплексным сложением и комплексным умножением с плавающей точкой.
Если в этом же примере сохранить вещественные части коэффициентов и задать им нулевые мнимые части, сделав все коэффициенты вещественными, неточность вычисления полинома в наибольшем по модулю корне уменьшится на два десятичных разряда. Остальные – еще один вещественный и две пары комплексно сопряженных корней – обратят полином в ноль в данном формате вывода.
Для того чтобы получить эти результаты, надо заново найти границы вещественной и мнимой части корней согласно (17). В случае вещественных коэффициентов для первичного задания границ области корней достаточно взять максимальный по модулю коэффициент, сложить модуль с единицей и решить задачу с увеличенным радиусом локализации. По виду приближений корней затем устанавливаются уточненные границы вещественных и мнимых частей, а также исходный радиус локализации не больший половины наименьшего расстояния между несовпадающими вещественными и мнимыми частями приближенных значений корней. Радиус локализации для уточнения меньше десятой части исходного радиуса.
В последнем примере радиусы локализации приближения и уточнения уменьшены до значений, с которыми решались все задачи этой части экспериментов.
Схема идентификации границ области корней и определения радиуса локализации
В общем случае границы вещественных и мнимых частей корней полиномов с явно заданными, вообще говоря, комплексными коэффициентами первоначально устанавливаются из (17), (18), причем использование (18) не необходимо. Максимум модулей коэффициентов из (17), сложенный с единицей, проектируется на вещественную и мнимую оси комплексной плоскости. Границы проекций принимаются в качестве приближений границ области с небольшим запасом в обе стороны от центра координат. Радиус локализации для процедуры identif1 приближения ('PRIBLIJENIE') принимается увеличенным примерно в 10 раз по сравнению с использованным в предыдущих программах. В пределах границ квадрата 20×20 можно брать этот радиус равным 0.49. В пределах квадрата 200×200 можно брать радиус на единицу больший (при малых значениях радиуса программа будет работать неприемлемо долго). Радиус процедуры identif1 уточнения ('TOCHNOE') берется десятой частью от радиуса приближения. С такими параметрами задача решается, результатом будут приближения корней. Посредством рассмотрения их вещественных частей в качестве уточненных границ выбираются наименьшее и наибольшее значение вещественной части всех различных приближений корней. Аналогично, в качестве уточненных границ выбираются наименьшее и наибольшее значение мнимой части всех различных приближений корней. В процессе рассмотрения отмечаются наиболее близкие друг к другу значения вещественных, а также мнимых частей не совпадающих приближений корней. За новый радиус локализации для последующей процедуры приближения принимается величина, меньшая половины модуля наименьшей разности этих значений. В зависимости от класса и степени полиномов этот радиус может быть уменьшен вдвое или в шесть раз. За новый радиус локализации для последующей процедуры уточнения принимается радиус, в десять раз меньший радиуса приближения, аналогично предыдущему, он может быть уменьшен вдвое или в шесть раз. Неправильный выбор границ и соответственного им радиуса локализации может проявить едва ли не самый существенный недостаток предложенного метода: при малом радиусе в больших границах (в комплексном случае) программа будет работать неприемлемо долго, при слишком завышенном радиусе пропустит корни и даст искаженное представление о структуре их расположения.
Изложенная схема выбора границ и радиусов допускает автоматизацию. Среди вещественных частей приближений корней ищется наименьшая и наибольшая в один проход цикла. Составляется массив разностей вещественных частей для каждого текущего приближения корня, и минимальное значение выбирается в двойном цикле по всем приближениям корней. Аналогично – для границ мнимой части и радиуса локализации. Очевидно, схема распараллеливается по всем приближениям корней.
При разбросе корней на комплексной плоскости предложенную схему можно применить несколько раз с соответственно убывающими параметрами. Кроме того, область корней можно разделить на подобласти с относительно близко расположенными корнями. В каждой подобласти корни ищутся без изменения метода.
Об идентификации корней полинома с двоичными коэффициентами
Коэффициенты полиномов равные либо нулю, либо единице задаются в подпрограмме func только в вещественной части, мнимая часть заполняется нулями, например,
bdv[n1]: = 1; bdv[n1-1]: = 1; bdv[n1-2]: = 0; bdv[n1-3]: = 1; bdv[n1-4]: = 0; bdv[n1-5]: = 1; bdv[n1-6]: = 1;
bmv[n1]: = 0; bmv[n1-1]: = 0; bmv[n1-2]: = 0;bmv[n1-3]: = 0; bmv[n1-4]: = 0; bmv[n1-5]: = 0; bmv[n1-6]: = 0;
В этом примере заданы коэффициенты полинома
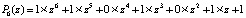 , (20)
, (20)
Согласно (17) для границ его корней достаточно взять значение 2: x00: = -2; x11: = 2; y00: = -2; y11: = 2; Запускается программа с увеличенным радиусом локализации eps0: = 0.49; h: = eps0/43/2; По результатам работы программы уточняются границы вещественной и мнимой части корней, определяется и уточняется радиус локализации:
eps: = 1e-44; mm: = 4; x00: = -1.6; x11: = 0.8; y00: = -1; y11: = 1; eps0: = 0.049/2/3; h: = eps0/43/2; eps00: = eps0;
Окончательные результаты вычисления корней полинома (20):
-1.506135679553838820000000000000
-0.000000000000000000000000000000 0.000000000000000000000000000000
-0.663950807072194900000000000000
0.000000000000000000000000000000 0.000000000000000000000000000000
-0.155553908732990950000000000000
-0.987827404700784920000000000000 0.000000000000000000000000000000
-0.155553908732990950000000000000
0.987827404700784920000000000000 0.000000000000000000000000000000
0.740597152046007810000000000000
-0.671949297478122520000000000000 0.000000000000000000000000000000
0.740597152046007810000000000000
0.671949297478122520000000000000 0.000000000000000000000000000000
Программа нашла две пары комплексно сопряженных корней и два вещественных корня. Ясно, что битовые значения коэффициентов не окажут существенного влияния на комплексные операции схемы Горнера при некоторых ограничениях степени полинома. В этом случае всегда будет точный (в формате представления данных) результат. Полином (20) соответствует двоичному числу 1×26 + 1×25 + 0×24 + 1×23 + + 0×22 + 1×2 + 1 = 1101011. Если предполагать, что в определенных границах степеней двоичных полиномов (разрядности двоичных чисел) предложенный метод всегда будет давать только правильные значащие цифры их вещественной и мнимой части, то найденные корни будут единственным образом соответствовать сопоставленному полиному и по транзитивности – двоичному коду.
Возникает вопрос, можно ли на основе предложенной программы при условии ограниченной разрядности целочисленных двоичных кодов конструктивно установить взаимно однозначное соответствие двоичных кодов и комплексных корней полиномов с коэффициентами соответственных двоичных полиномов? Если с некоторыми оговорками это возможно, то комплексные корни могут кодировать информацию. Сами коды восстанавливаются с помощью представленного выше алгоритма восстановления коэффициентов полинома по его корням. Аналогичный вопрос можно отнести к другим позиционным системам счисления.
Подводя итог, можно заключить, что предложенный метод идентификации корней полиномов отличается от известных [3, 4, 10, 13, 14] по построению на основе устойчивой адресной сортировки (сортировка слиянием по матрицам сравнений). Отличительные особенности характеризуются тем, что метод не требует отделения корней, область корней достаточно ограничить оценками Маклорена (или более грубыми оценками [9]), точность приближения сохраняет верные значащие цифры мантисс корней, в том числе в случае полиномов высоких степеней (до 14480 в случае вещественных корней, до 420 в случае комплексных корней). Метод обладает естественным и максимальным параллелизмом, что дополнительно отличает его от известных [15], отличия сохраняются по отношению к компьютерно-ориентированным методам вычисления корней полиномов [16–18].
Заключение
Изложен компьютерный метод идентификации корней полиномов на основе сортировки слиянием по матрицам сравнений. С помощью численных экспериментов показано, что метод идентифицирует все (в том числе плохо отделенные) вещественные корни полиномов до степени 14480 с верными знаками мантисс в формате данных extended. Метод идентифицирует все комплексные корни полиномов до степени 420 с верными знаками мантисс в том же формате. Правильная работа метода сохраняется в границах числового диапазона компьютера, при этом проявляется устойчивость к возмущению коэффициентов полинома. В случае комплексных корней ограничение создает время работы программы.



