Прикладной характер исследований в области классификации и кластеризации данных, широчайшая область задач, решение которых сводится к эвристическому выбору метода и подбору параметров, оставляет в тени теоретические обоснования этих методов. Между тем сильные расхождения в эффективности одного и того же алгоритма на разных наборах данных можно интерпретировать только на основании математически формализованной модели. Этим обусловлена актуальность работы по построению и исследованию теоретической модели процесса нечеткой классификации в рамках Байесовского подхода (НКБ).
Методологические подходы к конструкции алгоритма нечеткой кластеризации и вероятностного метода разделения Гауссовой смеси (англ. GMM) кажутся внешне схожими. В некоторых публикациях демонстрируется сходство получаемых результатов [1–3]. Однако в данных работах различие иллюстрируется на уровне методик применения, а не на уровне математически строгого определения вероятности.
Общность понятий «принадлежности» в методологии нечеткого логического вывода и «вероятности» в задачах разделения распределений ощущается исследователями на интуитивном уровне. В [4] анализ сходства этих понятий подвергается развернутому анализу и даже используется неформальное определение: «нечеткость – это замаскированная вероятность», однако сходство это только внешнее, так как «принадлежность» связана с реализацией случайной величины посредством понятия лингвистической переменной, выбор которой субъективен.
В работе [5] объясняется возможность встраивания байесовского статистического подхода в систему нечеткого вывода в рамках вероятностной логики, построив тем самым логико-вероятностную модель классификатора. Работа [6] в рамках этого направления посвящена результирующему этапу процесса нечеткого вывода – фаззификации. В этих работах множество лингвистических переменных ассоциировано с множеством байесовских гипотез. Каждая гипотеза соответствует утверждению об определенном значении выходной лингвистической переменной из своего терм-множества. В [5] приводится также сравнение результатов дефаззификации на основе апостериорной байесовской вероятности с алгоритмом нечеткого вывода Мамдани.
Целью исследования, таким образом, является построение вероятностной модели нечеткой классификации, чтобы синтезировать алгоритм, объединяющий нечеткий и вероятностный подход в рамках теории вероятности. В данной работе описывается математическая вероятностная модель, которая служит основой расчетного алгоритма, приводятся результаты предварительного вычислительного эксперимента на модельных данных. Также с помощью вероятностной формализации модели нечеткого вывода устанавливаются глубокие различия между задачей нечеткой классификации и задачей разделения смеси распределений, так как им соответствуют разные вероятностные модели [6].
Материалы и методы исследования
Задача четкой классификации является задачей построения разбиения множества данных Х. Нечеткую классификацию можно представить как задачу построения открытого покрытия ⋃jUj множества данных, так как каждый элемент множества U может содержаться сразу в нескольких множествах покрытия Uj с различными значениями функции принадлежности. Отличие от вероятностного подхода в задаче разделения распределений, состоит в том, что ни одно из этих множеств не является выборкой из генеральной совокупности, имеющей теоретическое распределение.
Каждому элементу покрытия Uj сопоставим так называемый центр yj. Каждому элементу хn исходного множества данных сопоставимо значение принадлежности pri,j какому-либо элементу покрытия. В терминах нечеткой логики это значение функции принадлежности. Под принадлежностью понимается мера близости этого элемента к центру класса yj. Каждый элемент покрытия соответствует множеству термов выходной логической переменной. Искомое открытое покрытие должно обладать свойством оптимальности, в том смысле, что общее взвешенное расстояние принадлежности каждой точки данных xn к прототипу каждого множества yj должно быть минимальным.
Таким образом, принадлежности трактуются как аргументы вероятностных логических функций в системе вероятностной логики. Нечеткие продукции в системе логического вывода преобразуются в вероятностные логические функции, а их значения понимаются как условные вероятности в определении апостериорного распределения. Понятие условной вероятности близко определению продукции, которая является импликативной логической функцией: при выполнении посылок продуктивного правила заключения отражают степень уверенности в том, что выходная лингвистическая переменная принимает то или иное значение из множества термов.
Формальное преобразование логической функции, представленной в нормальной форме, в функцию вероятностной логики следующее: логическим переменным ставятся в соответствие p1, p2, …, pm элементарных событий, соответствующим атомарным формулам. При этом инверсиям переменных соответствуют значения 1 – pi. Конъюнкции и дизъюнкции соответствуют арифметическим операциям умножения и сложения.
На этапе дефаззификации [6] для каждой выходной лингвистической переменной на множестве гипотез о принятии значения из своего терм-множества по формуле Байеса вычисляется распределение апостериорных вероятностей.
Вероятностные модели байесовского нечеткого классификатора (НКБ) и гауссовой смеси
Неизвестные значения принадлежностей множества prnj и прототипы множеств yj (центры классов) трактуются как случайные величины X|U и Y соответственно. Далее выбирается некоторое эмпирическое распределение для каждой из них и устанавливается наиболее вероятное значение для сделанной выборки.
Пусть N – количество точек данных, D – размерность пространства данных, J – количество классов. Обозначим prnj принадлежность точки хn классу j, m – параметр фаззификации [6–8], yj прототип (центр) класса с номером j. Ясно, что значения наблюдаемых данных представляются матрицей размера D×N, значения принадлежностей U представляются матрицей размера J×N, а значения прототипов представляются матрицей размера D×J.
Совместное распределение данных по классам и центров классов по множеству данных является вероятностной моделью БНК. Оно задается тремя распределениями: совместным распределением многомерных случайных величин X|U и Y, априорным распределением прототипов и классов (вероятность того, что определенный прототип задает класс) и распределением прототипов по данным, т.е. вероятность того, что точка из множества данных является прототипом класса.
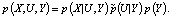(1)
Определим каждый из этих сомножи- телей.
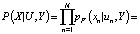(2)
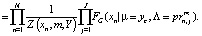
Это фактически означает, что каждое наблюдаемое значение попадает в какую-либо нормально распределенную выборку с некоторой «уверенностью»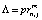 
различной для каждого значения xn. Количество таких выборок равно числу классов J. Z(un, m, Y) – это нормирующий множитель, зависящий от параметров выборочного нормального распределения и параметра фаззификации.
Прототип полагается нормально распределенной величиной
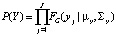(3)
с параметрами
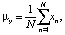
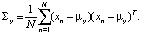
Далее, априорная вероятность того, что определенный класс задается определенным прототипом, имеет распределение:
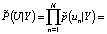(4)
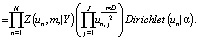
Здесь первый множитель – произведение констант нормализации, при этом использование евклидовой нормы не является обязательным [6, 7].
Относительно второго произведения необходимо отметить, что оно относится к известному классу «неправильных приоров», так как распределение (4) не может быть нормализовано на интервале [0, 1], по крайней мере, для многих соответствующих значений m и D) [7].
Третий сомножитель в (4) – априорная вероятность прототипов классов, для ее представления используется распределение Дирихле, параметризованное вектором α.
Модель гауссовой смеси имеет принципиально иную вероятностную интерпретацию, чем предложенная модель НКБ.
Распределение гауссовой смеси представлено выражением
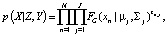(5)
где zn,j∈{0,1}, Σ zn,j = 1.
Сравнение вероятностных моделей
Переменные znj, для каждой точки xn представляют вероятность того, что данная точка лежит в классе с прототипом в точке μi. При этом остальные значения этих переменных равны нулю, так как в основе разделения смесей лежит предположение, что каждая точка является элементом выборки только одной генеральной совокупности с некоторым распределением. Сравнивая вероятность в (5) с выражением (1), очевидно, что нечеткий классификатор Байеса использует произведение всех вероятностей компонентов, что означает учет возможности попадания значения xn в различные классы. В этом состоит основное отличие рассматриваемых задач.
Так как обратная ковариация использует принадлежность как значение весовой переменной для каждого значения xn, то значения, полученные по модели НКБ, независимы, но их распределение неравномерно на множестве данных. В отличие от этого, модель разделения смеси предполагает независимость, но значения, получаемые по (5) в результате итерационного алгоритма, называемого ЕМ [8, 9], оказываются равномерно распределенными на исходном множестве.
Результаты вычислительного эксперимента на тестовом множестве точек данных
Целью проведенных расчетов является проверка работоспособности расчетной модели на различных значениях параметров алгоритма. На первом этапе эксперимент проводился на модельном наборе данных. В [7] подробно разобран алгоритм, который не использует итерационный пересчет значений на множестве данных, следовательно, расширяются возможности использования значения параметров метода, неразрешенных в методе с-средних. Реализация алгоритма представлена в [10]. Там же представлена реализация традиционного алгоритма с-средних.
Модельный набор данных состоял из двух двумерных нормальных выборок, содержащих 250 точек с различными параметрами. Параметры распределений: μ1 = (1, 2,5), и μ2 = (3, 1), ковариационные матрицы Σ1, Σ2 единичные. Параметр фаззификации был взят равным m = 1, а параметр распределения Дирихле α = 1.
При m = 3, m = 5 для тех же параметров нормальных выборок значения принадлежностей незначительно уменьшаются. Установка значения этого параметра должна связываться с параметрами нормального распределения. Для распределений с единичной ковариационной матрицей влияние изменения этого параметра не выявляется. Расчеты производились для единичного значения. Число пересчетов принадлежностей также не терпит критических изменений: использовалось 124 и 131 итерация для m = 3, m = 5 соответственно.
Было установлено, что реализация стандартного метода с-средних без реализации параллельных вычислений и реализация предложенной модели НКБ имеют схожие эмпирические показатели производительности, оба использовали чуть более 100 итераций.
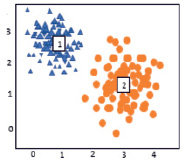
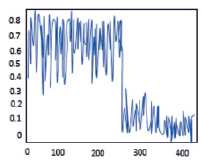
Рис. 1. Результаты кластеризации модельных данных
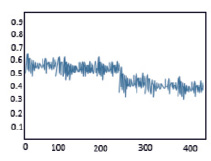
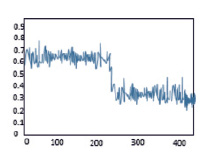
Рис. 2. Функции принадлежности для m = -10 (слева) , m = -5 (справа)
Вид функции принадлежности при расчетах по методу НКБ для изменённых значений m = -5 и m = -10, показанный на рис. 2, заставляет сделать вывод о том, что отрицательные значения параметра, определяющего, собственно, количественную оценку нечеткости классификации позволяют в некотором смысле «усреднить» значения принадлежностей для каждой точки модельного набора. С увеличением по модулю этого параметра растет число требуемых итераций и классы становятся более «размытыми» даже на модельном наборе. Можно предположить, что варьирование этого параметра должно проводиться совместно с изменением параметра α априорного распределения Дирихле. Взаимовлияние параметров распределений составляет самостоятельное направление исследований в этом направлении.
Заключение
Синтез байесовского подхода и нечеткого вывода является современным направлением в исследованиях решения задач классификации и кластеризации, этому посвящено немало публикаций в мировых научных изданиях.
Построенная вероятностная модель байесовской классификации имеет работоспособность не хуже традиционного метода с-средних на тестовых данных, кроме того, она имеет расширенные возможности в отношении значений параметров классификации.
Перспективные направления представленного исследования состоят прежде всего в применении построенной модели распределения в качестве инструмента дефаззификации в процессе нечеткого вывода. Представляет интерес теоретическая формализация связи построенной модели с алгоритмом нечеткого вывода, в особенности строгое представление связи между продукционными вероятностными функциями и параметрами распределения Дирихле при определении априорных вероятностей. Также возможен переход от классификации к более широкой задаче нечеткой кластеризации, так как прототипы классов в модели являются случайными величинами.
Другим направлением развития является детальное исследование влияния параметров на результаты алгоритма, в частности влияние параметров распределения Дирихле, используемого в качестве априорного распределения. Вычислительный эксперимент с изменением значения параметра m, определяющего «нечеткость» процесса, показал, что отрицательные значения m могут ухудшить работу алгоритма в целом, однако возможность гибкого изменения этого параметра полезна в усовершенствованном алгоритме для решения задачи кластеризации, когда число кластеров неизвестно заранее.
Проведенное сравнение модели задачи нечеткой байесовской классификации с задачей разделения смеси выявляет различие на уровне математической формализации. Однако построенная модель не лишена основного недостатка в сравнении c алгоритмом GMM: алгоритм на основе данной модели применяется лишь для «симметричных по координатам» классов данных. В дальнейших исследованиях целесообразно провести сравнение эффективности расчетных алгоритмов для обеих моделей с целью выявления влияния их различий на результаты классификации объектов с признаками различных типов: символьных, текстовых или числовых.