Изучение социально-экономических систем (СЭС) требует рассмотрения множества сложных процессов в экономике – инвестиционных, производственных, финансовых, управленческих, а также учета интересов различных участников – производителей, потребителей, управленцев, инвесторов, социума и пр., и поэтому весьма затруднительно без разработки математических моделей указанных процессов в целом, а также их участников в частности. Так как функционирование СЭС происходит во времени, то его полноценное описание требует использования динамических моделей [1] или комбинации динамических и статических моделей [2, 3]. В настоящее время сохраняется значительный поток публикаций, описывающих различные методы анализа моделей СЭС [4, 5], особенности функционирования макроэкономических [6] и мезоэкономических [7] систем, содержащих краткие обзоры моделей [8], а также освещающих другие содержательные аспекты развития СЭС. Вместе с тем большинство публикаций касается отдельно либо концептуальных вопросов моделирования, либо построения различных моделей СЭС, либо алгоритмов их численного анализа, и, соответственно, имеется незначительное количество работ системного характера, например [9], в которых рассматривается весь комплекс аналитических инструментов: концепция, математические модели, методы и алгоритмы их анализа, с выходом на разработку систем поддержки принятия решений (СППР). Следует отметить, что математические модели в приведенных выше публикациях имеют ряд особенностей, зачастую затрудняющих разработку соответствующих СППР, ориентированных на оперативную экспертную поддержку оптимальных решений при управлении развитием СЭС или выявление оптимального баланса циркулирующих в них потоков. В частности, в моделях [6, 7] рассматривается динамика экономического процесса в форме системы соотношений Р. Соллоу с заранее заданной возрастающей производственной функцией (преимущественно в виде Кобба – Дугласа), не выявляющей его жизненный цикл. Динамические модели, описанные, например, в [8], не являются оптимизационными, модель [9] является примером нелинейных задач экономической динамики, в которых, вообще говоря, затруднена разработка численных алгоритмов их анализа, устойчиво работающих с ростом размерности задачи, и т.д.
Материалы и методы исследования
Системный подход к изучению развития СЭС, на наш взгляд, является наиболее целесообразным, если имеется содержательно адекватная и достаточно универсальная общая модель СЭС, которая может быть подвергнута сбалансированному по скорости и точности расчетов численному анализу в условиях практически значимых размерностей. Это предполагает, в свою очередь, исследование теоретических вопросов доказательства существования решения задачи и тем самым обоснования возможности и целесообразности разработки СППР. В работе [3] описан комплекс инструментов (подход, модели, алгоритмы и системы поддержки принятия решений по управлению развитием СЭС), учитывающий перечисленные недостатки и явившийся результатом исследований, проводимых в Сибирском государственном университете науки и технологий (г. Красноярск) и Российском экономическом университете (Кемеровский институт) в течение 2005–2021 гг.
Развитие информационных технологий, очевидно, актуализирует разработку СППР в процессе управления сложными СЭС, что, в свою очередь, стимулирует разработку моделей и алгоритмов их численного анализа, сбалансированный комплекс которых может лежать в основе СППР, востребованных конечными пользователями. Ниже рассматриваются сформулированные в рамках концепции работ [2, 3] содержательная постановка задачи и новая математическая модель оптимального управления функционированием СЭС в форме многошаговой задачи линейного программирования (МЗЛП) вида
x(t + 1) = A(t)x(t) + B(t)u(t) – s(t); x(0) = a,
C(t)x(t) + D(t)u(t) ≤ h(t); ul(t) ≥ 0;
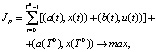
где u(t) = [ul(t)] и x(t) = [xi(t)] – управляющий и фазовый векторы соответственно; A(t) = [aij(t)]; B(t) = [bil(t)]; C(t) = [ckj(t)]; D(t) = [dkl(t)]; a = [ai]; s(t) = [si(t)]; h(t) = [hk(t)]; a(t) = [ai(t)]; b(t) = [bl(t)]; (i, j = 1,...n; l = 1,...rt; k = 1,...mt; t = 0,...T0); rt, mt и T0 – размерность вектора u(t), количество ограничений и шагов соответственно; (‧,‧) – операция скалярного произведения векторов. МЗЛП может решаться с помощью алгоритмов, основанных на оптимизационных принципах Беллмана и Понтрягина, с помощью методов теории дифференциальных игр [4]. Применяя к представленной МЗЛП z-преобразование, ее можно привести к соответствующей задаче линейного программирования (ЗЛП) как на бесконечном [2], так и на конечном [5] горизонтах планирования, причем полученная ЗЛП сохраняет ряд фундаментальных свойств исходной динамической задачи, с одной стороны, а с другой – позволяет разрабатывать эффективные алгоритмы ее теоретического и численного анализа [3]. В работе [10] изложен алгоритм численного решения МЗЛП симплекс-методом путем перехода к эквивалентной ЗЛП большой размерности.
Охарактеризуем социально-экономическое содержание решаемой задачи. Пусть в территориально-производственной системе рассматривается инвестиционно-производственный проект (ИПП), в котором предполагается производство продукции (товаров и/или услуг) n видов с заданными рыночными ценами ее единицы и стоимостными оценками спроса, причем каждый вид продукции, в соответствии с принципом чистых отраслей, производится с использованием n комплектов основных производственных фондов (КОПФ) заданной стоимости, сроков полезного использования и производительности. Проект реализуется в несколько этапов: начальный, инвестиционный, инвестиционно-производственный и производственный (постинвестиционный). Указанная система функционирует в условиях, связанных с ограниченностью используемых ресурсов инвестиционного, производственного, финансового, социального характера. Необходимо определить (как в целом, так и по отдельным видам продукции) оптимальные суммы инвестиций, объемы производимой продукции каждого вида, а также режимы финансирования процессов в СЭС, при которых максимизируется дисконтированная добавленная стоимость рассматриваемого проекта на заданном горизонте планирования. В качестве экономических агентов СЭС, как правило, выступают разнообразные производственные и территориально-производственные структуры (предприятия, территории, их объединения в форме корпораций, холдингов, отраслей, кластеров и пр.), а также социум и региональный управляющий (налоговый) центр. При взаимодействии указанных экономических агентов возникает конфликт интересов, обусловленный тем, что в рыночной экономике целью производственных структур является максимизация прибыли или другого показателя качества экономической деятельности, тогда как основная экономическая цель управляющего центра – максимизация налоговых поступлений в бюджет от деятельности производителя, а социума – увеличение своего благосостояния, экономической основой которого является оплата его труда, которые, в свою очередь, снижают прибыль производителя. Иначе говоря, так как доходы одних агентов являются расходами других, многокритериальное принятие управленческих решений является необходимым даже в относительно простом случае двух или трех участников соответствующего процесса. Помимо этого, в социально-экономических процессах существенными, определяющими направление их развития, становятся такие факторы, как необходимость достаточной для обеспечения комфортной жизни социума сохранности окружающей природной среды и планеты в целом. Сложность рассматриваемой глобальной задачи и заставляет исследователей разрабатывать математические модели, эффективные алгоритмы их анализа и программно-аналитические комплексы поддержки принятия инвестиционных, производственных и финансовых решений при управлении СЭС [3, 11].
Результаты исследования и их обсуждение
Приведем результаты формализации описанной выше задачи оптимального управления СЭС, состоящей из производственно-территориальной системы и налогового центра (НЦ). Здесь и далее (если не указано особо) счетчик k пробегает значения от 1 до n или, иначе, k = 1,…,n. Пусть uk(t) (t = T2,…,T-1), un+k(t) (t = T2,…,T-1), u2n+1(t) (t = 0,…,T-1), u2n+2(t) (t = 0) – соответственно стоимость приобретаемых КОПФ и выручка от продажи продукции k-го вида, кредиты и дотации на обеспечение проекта функционирования СЭС; xk(t), xn+1(t) xn+2(t) xn+3(t) (t = 0,…,T) – соответственно накопленная стоимость КОПФ k-го вида, остаточная стоимость всех КОПФ, текущие денежные средства предприятия и накопленные суммы кредитов в момент t; Pk(t), Vk(t), Tk(t), ck(t), δk(t) = Pk(t)Vk(t)/ck(t) (t = 1,…,T) – соответственно рыночная цена единицы продукции, производительность, срок полезного использования, стоимость, фондоотдача КОПФ k-го вида в моменты t; qk(t + 1) (t = T2,…,T-1) – прогнозный спрос на продукцию k-го вида в стоимостном выражении для момента t+1; I0, K0, D0 – соответственно максимальные суммы инвестиций, кредитов и дотаций, выделяемых на весь срок действия ИПП; αi (I = 1,…,5) – соответственно ставки налогов на добавленную стоимость (НДС), на имущество (НИ), на прибыль (НП), взноса в страховые социальные фонды, а также определяемая спецификой проекта совокупная ставка других налоговых и неналоговых затрат; 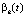 – доля общепроизводственных затрат, выделяемая на фонд оплаты труда (ФОТ) при производстве продукции k-го вида в момент t;
– доля общепроизводственных затрат, выделяемая на фонд оплаты труда (ФОТ) при производстве продукции k-го вида в момент t; 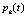 – доля общепроизводственных затрат, относимая на оборотные затраты при производстве продукции k-го вида в момент t; T1,T2,T (1 ≤ T2 ≤ T1 ≤ T) – соответственно моменты завершения инвестиций, начала производства и срок действия ИПП; r1, r2, rср, r0 – годовые ставки дисконтирования потоков ИПП в периоды установки оборудования (строительства), производства и кредита соответственно; δ (0 ≤ δ ≤ 1) – экспертно определяемая доля остаточной стоимости всех КОПФ от ее балансовой стоимости на момент t = T. Математическая модель сформулированной задачи описывается следующей системой соотношений:
– доля общепроизводственных затрат, относимая на оборотные затраты при производстве продукции k-го вида в момент t; T1,T2,T (1 ≤ T2 ≤ T1 ≤ T) – соответственно моменты завершения инвестиций, начала производства и срок действия ИПП; r1, r2, rср, r0 – годовые ставки дисконтирования потоков ИПП в периоды установки оборудования (строительства), производства и кредита соответственно; δ (0 ≤ δ ≤ 1) – экспертно определяемая доля остаточной стоимости всех КОПФ от ее балансовой стоимости на момент t = T. Математическая модель сформулированной задачи описывается следующей системой соотношений:
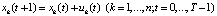 , (1)
, (1)
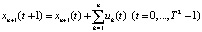 , (2)
, (2)
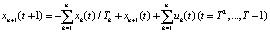 , (3)
, (3)
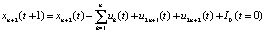 , (4)
, (4)
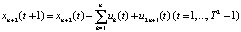 , (5)
, (5)
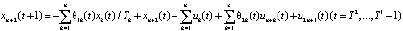 , (6)
, (6)
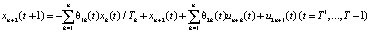 , (7)
, (7)
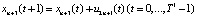 , (8)
, (8)
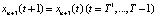 , (9)
, (9)
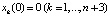 , (10)
, (10)
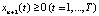 , (11)
, (11)
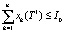 , (12)
, (12)
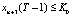 , (13)
, (13)
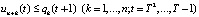 , (14)
, (14)
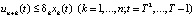 , (15)
, (15)
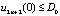 , (16)
, (16)
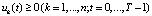 ,
, 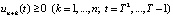 , (17)
, (17)
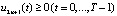 ,
, 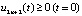 , (18)
, (18)
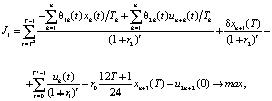 (19)
(19)
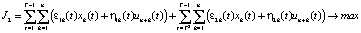 , (20)
, (20)
где J1, J2 – соответственно дисконтированные суммы собственных средств производителя и НЦ,
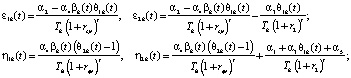
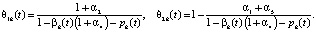
Рассмотрим содержательный смысл соотношений в модели (1)–(20). Уравнения (1) описывают динамику накопленной стоимости КОПФ каждого из n видов, (2), (3) – динамику суммарной остаточной стоимости всех КОПФ соответственно на допроизводственной и производственной стадиях ИПП, (4)–(7) – уравнения движения текущих денежных средств производителя в момент t = 0, на допроизводственной стадии, на стадии производства с доинвестированием (реинвестированием) и на постинвестиционной стадии ИПП соответственно; (8), (9) – накопленные суммы кредитов на допроизводственной и производственной стадиях; (10) – начальные условия на фазовые переменные. Неравенства (11) отражают требования неотрицательности финансовых средств ИПП на всем горизонте планирования, (12) – ограничения на сумму инвестиций в производство всех видов продукции в момент t = Т1, (13) – ограничение суммы кредитов на финансирование текущего производства на момент окончания ИПП, (14) – требования непревышения выручки от продажи продукции k-го вида верхней оценкой стоимостного спроса на нее в период производства, (15) – условия непревышения выручки от продажи продукции k-го вида производственных мощностей в период производства, (16) – ограниченность объема осуществленных дотаций в начальный момент реализации ИПП; (17)–(18) – суть содержательно естественные условия неотрицательности управляющих переменных. Условие (19) – критерий J1 производителя в СЭС отражает сальдо суммы дисконтированных потоков прибыли плюс остаточная стоимость КОПФ в последний момент реализации ИПП (по ставке r2) и, соответственно, вложенных инвестиций (по ставке r1) с учетом осуществленных в начальный момент дотаций и платы за кредитный ресурс на всем горизонте планирования. Условие (20) – критерий J2 управляющего налогового центра в СЭС представляет собой дисконтированные суммы налоговых и неналоговых сборов в допроизводственный период (по ставке rср = (r1 + r2)/2) и в производственный период до окончания проекта (по ставкам r2 и rср). Отметим, что, в отличие от ранее опубликованных динамических моделей СЭС [2, 3], в представленной модели источники финансирования ИПП разделены на две части – стратегическую (инвестиции) и тактическую (кредитование текущей производственной деятельности). Это предопределило некоторую смену трактовки как управляющих, так и фазовых переменных задачи, по сравнению с указанными моделями. В частности, управляющая переменная u2n+1(t) содержит информацию об оптимальных размерах кредитов в момент t реализации ИПП, а переменная xn+3(t) – о накопленных в течение горизонта планирования Т суммах кредитных средств. В модели (1)–(20) содержательно рассматривается динамика основных циркулирующих в СЭС экономических потоков – инвестиционного, производственного и финансового, которые формируются по правилам бухгалтерского учета через основные характеристики производимой продукции, производственных и финансовых активов. Модель (1)–(20) учитывает закон убывающей во времени стоимости финансового ресурса, в ней рассматриваются различные способы финансирования проектов (собственный и заемный капитал, кредитование, дотирование и пр.). Производственная функция является алгоритмически вычисляемой и способна отражать жизненный цикл развития СЭС. Нетрудно проверить факт, что нулевой управляющий вектор О(2n+2)×1 является частным решением задачи, описываемой соотношениями и условиями (1)–(20), а множество ее допустимых решений является компактом, что гарантирует существование решения указанной задачи для всех допустимых значений входящих в нее параметров. Согласно [12, 13], двухкритериальная МЗЛП (1)–(20) может быть сведена к эквивалентной однокритериальной линейной задаче с теми же ограничениями и максимизацией выпуклой линейной комбинации критериев J(µ) = µ1J1 + µ2J2, где 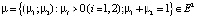 , E2 – двумерное евклидово пространство. Учитывая, что система (1) является математическим аналогом предложенных в работах [2, 3] динамических моделей СЭС, с вышеуказанными отличиями в содержательном смысле управляющих и фазовых переменных, наличие ее нетривиальных решений может быть проверено с использованием подробно описанного в [3] программного комплекса «Линейная динамика», позволяющего проводить полный параметрический анализ МЗЛП.
, E2 – двумерное евклидово пространство. Учитывая, что система (1) является математическим аналогом предложенных в работах [2, 3] динамических моделей СЭС, с вышеуказанными отличиями в содержательном смысле управляющих и фазовых переменных, наличие ее нетривиальных решений может быть проверено с использованием подробно описанного в [3] программного комплекса «Линейная динамика», позволяющего проводить полный параметрический анализ МЗЛП.
Заключение
Динамическая модель (1)–(20) отражает стратегические интересы и оптимальные инвестиционные, производственные и финансовые потоки основных участников проектов развития СЭС и, вместе с эффективными алгоритмами ее анализа, может явиться теоретически и численно сбалансированным инструментарием разработки автоматизированных систем поддержки принятия решений (в том числе оперативных) при управлении сложными социально-экономическими объектами.



