Зимние Олимпийские игры (ОИ) – самые крупные международные соревнования по зимним видам спорта. Проводятся Международным олимпийским комитетом (МОК) один раз в четыре года. На предстоящих XXIV Зимних Олимпийских играх (ОИ), которые пройдут в столице КНР г. Пекине будет представлено 15 видов спорта [1]. Во всех этих видах примут участие и спортсмены сборной Олимпийского комитета России (ОКР) [2].
Одной из главных и наиболее известных мер оценки результата национальной команды на Олимпийских играх является место в неофициальном командном зачете (НКЗ). НКЗ формируется по количеству золотых медалей либо по общему количеству медалей, которое выиграет команда. Официально НКЗ не признается организаторами игр, однако на сайте Олимпиады имеется возможность просмотра НКЗ в зависимости от различных критериев (золото, серебро, бронза, общее количество). Практически вся национальная спортивная система России (да и большинства других стран) в течение одного олимпийского четырёхгодичного цикла занимается подготовкой к следующим играм. По окончании игр результаты НКЗ оцениваются национальными спортивными федерациями, спортивными чиновниками из министерства спорта и большинством средств массовой информации (СМИ). Исходя из результатов оценки и делается вывод об успешности выступления.
Как правило, Национальный олимпийский комитет ставит перед олимпийской сборной определенный медальный план. Прогнозирование и планирование результатов медального плана требует материально-технических и экспертных ресурсов для обработки имеющихся данных и их анализа. Инструментом обработки большого объёма данных могут выступать различные математические методы и алгоритмы: методы Data Science [3], в том числе методы машинного обучения [4], аналитические и экспертные методы, средства и технологии прикладного искусственного интеллекта (ИИ) [5] и т.д. Одним из таких средств являются искусственные нейронные сети (ИНС). В предыдущих работах авторами описаны процедуры осуществления прогнозов в мультиспортивных событиях, где в качестве главного механизма формирования прогноза выступали сети с радиально-базисными функциями (RBF) и обобщенно-регрессионные нейронные сети (GRNN). Однако при подготовке обучающих выборок (ОВ) в индивидуальных видах спорта для данных ИНС возникают серьёзные проблемы, влияющие на точность прогнозирования. Кроме того, крайне важной задачей становится определение основных прогнозоформирующих факторов. Для решения указанных проблем авторами предлагается подход на основе ассемблирования (в частности, каскадирования) нескольких типов ИНС с анализом результатов в контрольных точках при поярусной обработке данных. В качестве объекта прогнозирования выбрано выступление сборной ОКР на XXIV Зимних Олимпийских играх.
Целью проводимых исследований являются оптимизация и повышение точности процесса планирования спортивной подготовки сборных команд и прогнозирование неофициального медального зачёта в мультиспортивных состязаниях с использованием системы на основе ассемблирования (каскада) ИНС.
Материалы и методы исследования
В предыдущих работах [6, 7] подробно описан процесс создания модели и прототипа программной системы, основанной на конвейеризации нескольких обрабатывающих модулей, причём каждый модуль уже содержит заранее обученную модель ИНС. При прогнозировании многопараметрических событий, например, достижений в индивидуальных видах спорта, обучающая выборка должна быть разбита на отдельные фрагменты, соответствующие типу ИНС в модуле. При этом фрагменты выборок могут полностью совпадать (дублироваться), совпадать частично или полностью отличаться. Предметное содержание фрагментов выборки может быть уникальным для каждого вида спорта или даже для каждого спортсмена.
На первом этапе исследований при проведении экспериментов с прототипом системы, содержавшим только GRNN-сеть, либо только RBF-сеть [7–10], были выявлены следующие проблемы. Поскольку обобщенно-регрессионная нейросеть представляет собой, по сути, разновидность радиальных базисных нейронных сетей, то механизмы прогнозирования при её использовании обычно основаны на непараметрической регрессии [8]. Первый промежуточный слой сети GRNN состоит из радиальных элементов. Второй промежуточный слой содержит элементы, которые помогают оценить взвешенное среднее. Процесс обучения GRNN-сети аналогичен обучению RBF-сети. Первоначально настраиваются центры базисных функций, а затем с фиксированными параметрами RBF-нейронов обучается выходной слой. Идея состоит в том, что каждая обучающая выборка будет представлять собой среднее значение для радиального базового нейрона. Конечно, GRNN имеет некоторые преимущества: однопроходное обучение, высокая точность оценки благодаря использованию функций Гаусса и т.д. Однако основным недостатком GRNN-сети при прогнозировании является её размерность – для получения достойной точности требуется большое число нейронов в обоих слоях.
Нейронная сеть с радиально-базисными функциями (RBF) [9] строится с использованием радиальных нейронов, функция активации которых имеет ненулевые значения только в окрестностях своего центра. Поэтому аппроксимация с помощью таких сетей называется локальной аппроксимацией. Сеть с радиально-базисными функциями имеет двухслойную структуру. Первый слой составляют радиальные нейроны, выходной слой – один или несколько линейных. Процесс обучения радиальной сети состоит из двух этапов. Укрупненно они выглядят следующим образом.
1) осуществляется подбор параметров радиальной функции для каждого радиального нейрона (в случае функции Гаусса – это центр и параметр ширины).
2) проводится подбор весов выходного слоя нейронов, второй слой сети производит оценку взвешенного среднего и определяет близость обучающего примера к локальному центру. Результат работы сети – значение степени близости входного вектора и локального центра.
Обучающая выборка для исследования функционирования указанных ИНС была сформирована на основе открытых источников из сети Интернет [11]. Обрабатываемые данные включают в себя наборы базовых и специализированных параметров главных претендентов на НКЗ начиная с 1979 г. (начало подготовки к Зимним ОИ 1980 г. в США). В соответствии с рекомендациями по формированию обучающих выборок, описанными в работах [12–14], выборка должна содержать данные о количестве видов спорта, в которых получены олимпийские лицензии спортсменами, результатах выступления спортсменов на мировых и европейских форумах, проводимых в преддверии Олимпиады, количестве жителей, ВВП на душу населения и т.д. Необходимо учитывать и фактор домашнего выступления сборных команд. Результирующий вектор, в зависимости от задачи прогноза, содержит либо место, занятое командой в общекомандном зачёте, либо количество выигранных золотых (серебряных, бронзовых) медалей в виде целого числа. Полная обучающая выборка содержит векторы, соответствующие определённым зимним ОИ. Фрагмент результирующих векторов приведен на рис. 1.
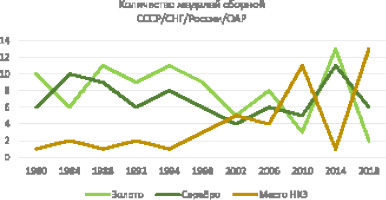
Рис. 1. Фрагменты результирующих векторов
Для проведения экспериментов в среде MATLAB разработаны два модуля, один из них на основе GRNN-сети, другой – на основе RBF-сети. Результаты экспериментов подробно рассмотрены в следующем разделе. Проблемой является невозможность учитывать динамически изменяемые (вновь получаемые) данные, которые могут существенно повлиять на результат прогноза. В данном случае, получая прогнозное значение золотых или серебряных медалей в НКЗ, невозможно добавить эти значения в какой-либо фрагмент обучающей выборки и вновь подать для обработки в GRNN или RBF-сеть. Ввиду особенностей рассматриваемых моделей их структура формируется под конкретную обучающую выборку. Если в первоначальной выборке не учитывался определенный предиктор (параметр), то невозможно добавить новый параметр в обучающую выборку. Это возможно только в процессе дообучения (переобучения) сети, а следовательно, потребуется формирование и новой структуры сети. В предложенной выборке параметры «количество серебряных медалей» и «количество бронзовых медалей» не учитывались, тогда как обычно место в НКЗ при равенстве у команд золотых медалей определяется по количеству медалей более «низкого достоинства».
Применение каскада из модулей предполагает динамическое формирование промежуточных прогнозных значений, передачу их с одного яруса на другой и формирование итогового прогноза на основе набора промежуточных прогнозных значений. При этом все предикторы на первом ярусе каскада разбиваются на количество, равное количеству модулей первого яруса. Как уже было отмечено выше, на всех ярусах для каждого модуля обучающая выборка формируется отдельно, и модули обучаются заранее. Пример структуры каскада для рассматриваемого в работе эксперимента приведен на рис. 2.
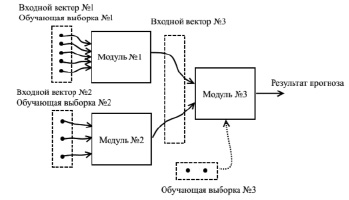
Рис. 2. Пример структуры каскада
Сформированная заранее обучающая выборка разбита на две части. В данной работе вариант разбиения основан только на экспертных оценках специалистов из ведущих федераций зимних видов спорта. Однако работоспособных вариантов может быть несколько, и в дальнейших экспериментах будут применяться подходы на основе метода определения предиктивных факторов, разрабатываемого авторами в настоящее время. Первая обучающая выборка (рис. 2) содержит «спортивные» составляющие, такие как количество видов спорта, выбранных для данных ОИ, количество олимпийских лицензий у спортсменов определённой страны, результаты спортсменов перед Олимпиадой и т.п. Вторая обучающая выборка – это социальные показатели, отмеченные ранее (население, ВВП и т.п.). Третья обучающая выборка включает данные, сформированные на основе результирующих векторов предыдущих ярусов. Например, она содержит информацию о количестве золотых, серебряных и бронзовых медалей, которые «скорее всего» будут завоёваны спортсменами страны на предстоящей Олимпиаде. Дополнительными данными в третьей выборке являются векторизованные наборы экспертных параметров. Результирующим вектором для третьей выборки будет вектор, содержащий места в НКЗ, что и является целью применения прогнозной системы. Логическое разбиение ОВ представлено на рис. 3.
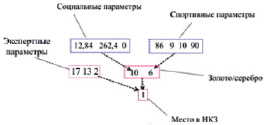
Рис. 3. Вариант разбиения на три обучающие выборки
Авторами были спроектированы и реализованы в среде MATLAB различные конфигурации каскадов системы прогнозирования. Полученные программные модели занимают не более 6 Мбайт на жестком диске.
Результаты исследования и их обсуждение
Эксперименты проводились на модели системы спортивного прогнозирования, имеющей двухъярусную структуру (рис. 2) н реализованную в среде MATLAB с использованием пакета Neural Network Toolbox. Нейронные сети RBF и GRNN были обучены с использованием рассмотренных в предыдущем разделе выборок.
Для анализа эффективности каскадирования модулей в табл. 1 представлены результаты работы «одномодульных» решений, на основе RBF-сети и GRNN-сети соответственно. Результаты RBF-сети представлены относительно параметра сглаживания (SPREAD), результаты GRNN-сети представлены относительно значений целевой ошибки обучения.
Таблица 1
Результат работы отдельных сетей
|
RBF-сеть |
|||
|
SPREAD |
Результат прогноза (место) |
Результат прогноза (золото) |
Результат прогноза (серебро) |
|
0,003 |
1 |
2 |
4 |
|
0,3 |
1,471 |
3,279 |
5,5134 |
|
3 |
2,24 |
6 |
6,2724 |
|
GRNN-сеть |
|||
|
Целевая ошибка |
Результат прогноза (место) |
Результат прогноза (золото) |
Результат прогноза (серебро) |
|
0,001 |
4 |
8 |
6 |
|
0,01 |
4 |
8 |
6 |
|
10 |
5,4728 |
6,9642 |
6,3989 |
Для RBF-сети минимальная среднеквадратичная ошибка (MSE) обучения получена при значении параметра SPREAD = 0,003. При увеличении параметра более 0,3 MSE возрастает. Для GRNN-cети при увеличении параметра целевой ошибки более 1, минимальная среднеквадратичная ошибка обучения начинает возрастать, результат прогноза при этом искажается. Прогноз RBF-сети некорректно отражает возможный исход соревнований. Место в НКЗ для сборной ОКР, очевидно, не может быть первым всего при двух золотых медалях. Данная ситуация демонстрирует проявление следующей проблемы. Невозможность корректно оценивать результат медального прогноза (количество медалей находится в результирующих векторах, а не в основной выборке) и прогнозировать с учётом этой «появляющейся» информации место в НКЗ. При использовании указанных моделей ИНС, чтобы добавить вновь полученные данные в обучающую выборку, придётся изменять её структуру. Такая возможность может быть не у каждого конечного пользователя программной системы.
Для повышения точности прогнозирования спортивных событий необходимо использовать системы с возможностью ассемблирования работающих модулей на основе различных моделей ИНС. Для предложенной структуры каскада (рис. 2) возможно несколько конфигураций системы. В данной работе рассмотрены четыре варианта архитектурно-структурных решений (рис. 4). В первом варианте на первом ярусе располагаются GRNN-сети, а на втором ярусе – RBF. Второй вариант предполагает размещение RBF-сетей на первом ярусе и GRNN – на втором. Третий и четвертый варианты – это каскады из сетей одинаковых моделей соответственно.
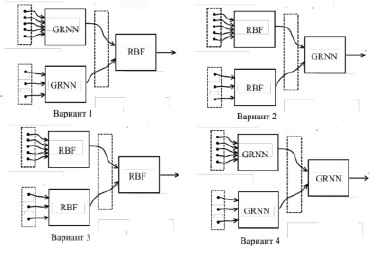
Рис. 4. Рассматриваемые конфигурации каскада
При построении системы прогнозирования с каскадной архитектурой для обучения модуля с радиально-базисными функциями используется значение SPREAD = 0,003, а для обучения модуля обобщенно-регрессионной нейронной сети – значение целевой ошибки, равное 0,001 соответственно. В ходе эксперимента значение параметров не изменяется. Фрагмент обучающей выборки для модуля первого яруса каскада, принимающего на вход спортивные параметры, приведен на рис. 5.
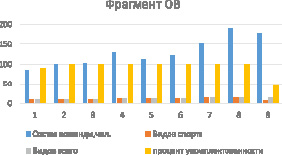
Рис. 5. Фрагмент обучающей выборки для модуля «спортивных параметров» первого яруса
Прогноз результатов выступления сборной ОКР на XXIV Зимних Олимпийских играх с использованием всех вариантов конфигурации каскада приведен в табл. 2. Прогноз будет считаться актуальным, если игры пройдут в определенный организаторами срок, а сборная ОКР закроет все имеющиеся лицензии, то есть выступит в полном составе.
Таблица 2
Прогноз выступления сборной ОКР
|
Каскад |
Результат прогноза (место) |
Промежуточный результат прогноза (золото) |
Промежуточный результат прогноза (серебро) |
|
Вариант 1 |
2 |
8 |
11 |
|
Вариант 2 |
11 |
2 |
4 |
|
Вариант 3 |
4,25 |
2 |
4 |
|
Вариант 3 |
4 |
8 |
11 |
Время обучения модулей в данной работе не рассматривалось, однако ни в одном из проведенных экспериментов время не превышало 52,6 с. Время непосредственной работы каскада составило менее 6,13 с. Учитывая, что данный прогноз является как минимум среднесрочным, такое время незначительно. Задача сокращения времени обучения и времени непосредственной работы каскада (или отдельной сети) будет крайне актуальна в случае необходимости краткосрочного и сверхкраткосрочного прогнозирования, например, при выполнении ставок в букмекерских конторах.
Заключение
Применение нейросетевых моделей, как по отдельности, так и с ассемблированием модулей, конечно, перспективно. Однако в некоторых случаях, при неполных или неправильно сформированных обучающих выборках, результат работы может оказаться, очевидно, недостаточно точным или даже некорректным. Частично эту проблему решает применение конфигурации сети на основе каскадирования и передачи динамически формируемых промежуточных прогнозных значений на последующие ярусы каскада. Уменьшение количества обрабатываемых параметров на первых уровнях системы позволяет сократить время обучения моделей и общее время получения прогноза. Использование предобработанных данных в модулях следующих уровней позволяет повысить точность прогнозирования, с учётом интерпретации задачи прогнозирования как задачи аппроксимации функции. Проблема предобработки обучающей выборки может быть решена классическими способами, например методом замены переменной (мода или медиана), методом отбрасывания неполных векторов и т.д.
Вторая проблема применения ИНС в прогнозировании – корректность обучающей выборки и определение наиболее значимых прогнозоформирующих предикторов. Данная проблема решается формированием отдельного «обучающего» алгоритма для формирования каскада, который определяет наиболее важные прогнозоформирущие предикторы после формирования основной структуры. Для определения ключевых предикторов используются промежуточные прогнозные данные на ярусах.
Имеющийся программный прототип системы прогнозирования на основе указанного подхода и используемых моделей продолжает дорабатываться и тестироваться [6]. Кроме того, по результатам испытаний разрабатывается алгоритм определения ключевых прогнозоформирующих предикторов, что позволит в дальнейшем значительно сократить объём как обучающих выборок, так и входных векторов для проведения прогнозирования. Сформулированы методические рекомендации по подготовке и структуризации обучающих выборок, а также особенностям применения различных моделей нейронных сетей в качестве инструмента спортивного прогнозирования.



