В последние годы появились исследования, посвященные изучению профессиональных дефицитов учителя математики, под которыми Л.В. Шкерина [1] понимает его профессиональные компетенции, которые отсутствуют или выражены недостаточно для эффективного осуществления образовательной деятельности, и в их составе выделяет предметные, методические и общепедагогические компетенции. О.В. Тумашева, М.Б. Шашкина и Е.А. Аешина [2], изучая профессиональные дефициты учителей математики в области преподаваемого предмета и методики обучения математике, выявили, что уровень предметной подготовки исследуемой группы педагогов не вполне соответствует современным запросам образования. Исследование Н. Подходовой и др. [3], посвященное оценке профессиональных компетенций учителя математики, показало, что учителя математики испытывают трудности с решением математических, педагогических или профессиональных проблем.
Логично предположить, что появление профессиональных дефицитов учителя математики связано с недостаточным формированием его профессиональных компетенций в вузе. При этом важно формирование как методических, так и предметных профессиональных компетенций. Л.А. Одинцова и О.В. Борисенко [4] полагают, что осознанное овладение обучающимися профессиональными компетенциями должно опираться на глубокое усвоение теоретического ядра знаний в сфере профильной подготовки.
Одним из средств повышения эффективности формирования профессиональных компетенций будущего учителя математики мы полагаем мониторинг, под которым понимаем систему регулярного отслеживания сформированности профессиональных компетенций студента, включающую сбор информации, ее хранение, обработку и распространение. Нам не удалось найти исследований, описывающих построение оценочных средств мониторинга профессиональных компетенций в соответствии с профессиональным стандартом педагога в применении к предметной подготовке будущего учителя математики.
Целью исследования является разработка и обоснование технологии создания оценочных средств мониторинга формирования профессиональных компетенций будущих учителей математики в процессе обучения математическим дисциплинам с учетом требований профессионального стандарта педагога.
Материалы и методы исследования
Цель исследования определила его методы, к которым относятся анализ научно-методической литературы и нормативных документов в сфере образования, использование компетентностного и деятельностного подходов как основы технологии разработки оценочных средств и методы наблюдения и анализа деятельности студентов в процессе применения оценочных средств мониторинга профессиональных компетенций.
Результаты исследования и их обсуждение
В статье [5] нами представлена модель мониторинга формирования профессиональных компетенций будущего учителя математики на основе профессионального стандарта педагога. Технология разработки оценочных средств включает определение диагностической цели оценочного средства и ее конкретизацию, определение показателей оценивания на основе анализа компетенций в соответствии с профессиональным стандартом педагога и ФГОС ВО 3++ по направлению «Педагогическое образование», составление спецификации оценочного средства, конструирование оценочного средства и разработку методических материалов по использованию оценочного средства, что согласуется с приведенной в [6] последовательностью этапов. Профессиональный стандарт влияет на все этапы технологии разработки оценочных средств мониторинга формирования профессиональных компетенций будущего учителя математики.
В целевом блоке модели [5] на основе выявленных требований профессионального стандарта педагога были сформулированы профессиональные компетенции, а затем и индикаторы их освоения. Отметим, что последние все еще остаются недостаточно конкретными для непосредственного диагностирования уровня сформированности компетенций. Необходимо описание достигнутых студентами уровней сформированности компетенций в рамках изучения отдельных дисциплин. Е.Н. Перевощикова [6] описывает прием переформулирования компетенций, суть которого с позиции деятельностного подхода состоит в согласованном описании компетенций и трудовых действий в виде опознаваемых и измеряемых действий обучающегося, в котором содержание компетенций раскрывается с учетом обобщенных трудовых функций педагога. Для согласования профессиональных компетенций с профессиональным стандартом педагога мы, как и Е.Н. Перевощикова [6], используем обобщенные трудовые функции «Педагогическая деятельность по проектированию и реализации образовательного процесса в образовательных организациях дошкольного, начального общего, основного общего, среднего общего образования» и «Педагогическая деятельность по проектированию и реализации основных общеобразовательных программ», но для разработки оценочных средств в соответствии с конкретизированными требованиями профессиональных компетенций мы берем в качестве основы модуль «Математика» профессионального стандарта педагога, поскольку диагностируем компетенции в математических дисциплинах.
В содержательном блоке модели [5] описаны последовательная конкретизация профессиональных компетенций в соответствии с требованиями профессионального стандарта Педагога и создание на их основе оценочных средств.
На примере дисциплины «Теория функций комплексного переменного» покажем соответствие требований профессионального стандарта педагога, индикаторов освоения компетенции ПК-1 и образовательных результатов по дисциплине (рис. 1). Элементы этой дисциплины входят в программу курса математики средней школы на углубленном уровне. В требованиях к результатам в Примерной образовательной программе среднего общего образования (одобрена решением федерального учебно-методического объединения по общему образованию (протокол от 28 июня 2016 г. № 2/16-з)) указывается, что обучающиеся будут иметь базовые представления о множестве комплексных чисел; применять при решении задач простейшие функции комплексной переменной как геометрические преобразования.
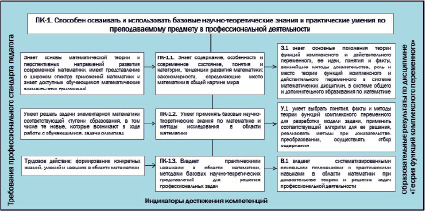
Рис. 1. Соответствие требований профессионального стандарта педагога, индикаторов освоения профессиональной компетенции ПК-1 и образовательных результатов по дисциплине «Теория функций комплексного переменного»
Для создания оценочных средств мониторинга мы конкретизировали требования компетенции в каждой теме дисциплины с опорой на профессиональный стандарт педагога. В частности, при конкретизации компетенции ПК-1 в теме «Последовательность комплексных чисел, ее предел. Функции комплексного переменного» мы ориентировались на такие трудовые действия учителя математики, как формирование конкретных знаний, умений и навыков в области математики, формирование внутренней (мысленной) модели математической ситуации (включая пространственный образ) и формирование у обучающихся умений пользоваться заданной математической моделью (формулой, геометрической конфигурацией, алгоритмом) и оценивать возможный результат моделирования, применять средства информационно-коммуникационных технологий в решении задачи; на умение педагога совместно с обучающимися создавать и использовать наглядные представления математических объектов (от руки на бумаге и классной доске или с помощью компьютерных инструментов), владение основными математическими компьютерными инструментами визуализации и вычислений (таблица).
Конкретизация требований компетенции ПК-1 в отдельных темах дисциплины «Теория функций комплексного переменного»
|
Образовательные результаты по дисциплине «Теория функций комплексного переменного» |
Конкретизация компетенции ПК-1 в теме «Последовательность комплексных чисел, ее предел. Функции комплексного переменного» |
|
З.1 знает основные положения теории функций комплексного и действительного переменного, ее идеи, понятия и факты, важнейшие методы доказательства, роль и место теории функций комплексного и действительного переменного в системе математических дисциплин, в системе общего и дополнительного образования по математике |
Знает понятия функции комплексного переменного, неподвижной точки линейного отображения, правила действий с комплексными числами в алгебраической и тригонометрической форме и их геометрическую интерпретацию, геометрические преобразования плоскости, связанные с линейной функцией комплексного переменного, инструменты динамической среды GeoGebra, выполняющие геометрические преобразования плоскости |
|
У.1 умеет выбрать понятия, факты и методы теории функций комплексного и действительного переменного для разработки модели задачи, применить соответствующий алгоритм для ее решения, реализовать методы при доказательстве, преобразовании, осуществлять отбор содержания |
Умеет верно интерпретировать условие задачи, используя понятия и факты теории функций комплексного переменного, строить геометрическую модель задачи, выполнять действия с комплексными числами и выражениями, содержащими комплексную переменную |
|
В.1 владеет систематизированными основными положениями и практическими навыками в области математики при доказательстве теорем и решении задач профессиональной деятельности |
Демонстрирует использование инструментов динамической среды GeoGebra, выполняющих геометрические преобразования, связанные с линейной функцией комплексного переменного |
На основе диагностичного представления компетенций была построена спецификация контрольно-измерительных материалов для измерения и оценки сформированности профессиональных компетенций будущего учителя математики.
Профессиональный стандарт педагога требует от учителя математики умения совместно с обучающимися создавать и использовать наглядные представления математических объектов и процессов, в том числе с помощью компьютерных инструментов, поэтому оценочные средства измерения уровня сформированности профессиональных компетенций должны отвечать требованиям наглядности и обеспечивать возможность применения информационно-коммуникационных технологий для решения задач.
В операционно-технологическом блоке модели [5] происходит применение оценочных средств и одновременно оценка их качества. Приведем пример задачи (рис. 2) и оценивания решений студентов в соответствии с конкретизированными требованиями.

Рис. 2. Пример задания из оценочных средств для мониторинга сформированности ПК-1

Рис. 3. Пример письменной работы студента, выполненной при решении задачи
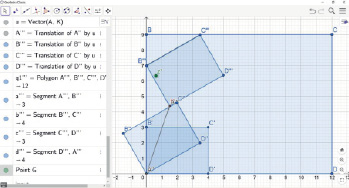
Рис. 4. Пример геометрической модели, выполненной студентом в динамической среде Geogebra при решении задачи
Мы оценивали сформированность компетенций ПК-1 путем анализа письменного решения задачи (рис. 3) и анализа файла с геометрической моделью, выполненной в динамической среде Geogebra (рис. 4).
Решение этой задачи потребовало от студента знания понятий линейной функции комплексного переменного, неподвижной точки линейного отображения, а также геометрических преобразований плоскости, связанных с линейной функцией комплексного переменного (параллельный перенос, поворот, гомотетия). Кроме того, студент продемонстрировал знание правил действий с комплексными числами в алгебраической и тригонометрической форме, геометрическую интерпретацию действий с комплексными числами. При построении геометрической модели студент показал знание инструментов динамической среды Geogebra, выполняющих геометрические преобразования фигур на плоскости.
В процессе решения задачи студент верно интерпретировал условие задачи, используя понятия и факты теории функций комплексного переменного, построил геометрическую модель задачи, выполнил действия с комплексными числами и выражениями, содержащими комплексную переменную. Интерпретируя условие задачи, студент установил, что меньшее изображение можно рассматривать как образ большего, полученного композицией трех преобразований – гомотетии, поворота вокруг точки и параллельного переноса, а композицию этих преобразований можно задать линейной функцией комплексного переменного, и доказательство существования искомой точки и ее построение свелось к нахождению неподвижной точки линейного преобразования.
При решении этой задачи, на примере двух самостоятельно выбранных изображений, студент продемонстрировал умение интерпретировать результаты, полученные с помощью инструментов динамической среды Geogebra, для реальных объектов.
Для выполнения решения задачи в динамической среде Geogebra студент выполнил необходимые построения и описал их, используя необходимую символику и обозначения, нашел координаты искомой неподвижной точки в Geogebra, используя подходящие инструменты, и на конкретных выбранных изображениях, используя измерительные инструменты.
Таким образом, анализ и оценка в соответствии с конкретизированными требованиями компетенции ПК-1 (таблица) представленного студентом решения задачи позволяет сделать вывод о высоком уровне сформированности у него компетенции ПК-1.
Результаты экспериментальной работы, косвенно также подтверждающей эффективность разработанных оценочных средств, описаны в нашей статье [5].
Заключение
Итак, мы представили технологию создания оценочных средств мониторинга профессиональных компетенций будущего учителя математики в преподавании математических дисциплин, все этапы которой ориентированы на профессиональный стандарт педагога, а именно на его модуль «Математика». Это означает, что для создания оценочных средств индикаторы освоения компетенций конкретизируются не только для отдельных дисциплин, но и для отдельных тем курса с опорой на анализ требований модуля «Математика» профессионального стандарта. Построенная таким образом спецификация позволяет разработать критерии оценивания профессиональных компетенций студентов с помощью разработанных оценочных средств. В соответствии с требованиями профессионального стандарта к учителю математики (трудовые действия, умения, знания), созданные нами оценочные средства обладают свойствами наглядности и адаптивности к использованию средств информационно-коммуникационных технологий.
Статья выполнена при финансовой поддержке ФГБОУ ВО «МГПУ им. М.Е. Евсевьева» по договору на выполнение научно-исследовательских работ от 27.07.2021 г. № 16-618 по теме «Мониторинг формирования профессиональных компетенций будущих учителей математики в условиях реализации профессионального стандарта педагога».



