В математике уже давно известны объекты (системы), обладающие, с одной стороны, простой структурой, с другой – демонстрирующие сложное поведение. Причем ощутить сложность в таких системах достаточно просто. Для первого знакомства вполне достаточно знаний школьной программы по математике и навыков проведения элементарных вычислений на компьютере. Весь спектр поведения в таких системах демонстрируется за три, четыре часа учебных занятий. Особенно важным здесь оказывается то, что в современной науке к подобным системам приковано большое внимание. Речь здесь в первую очередь идет об некоторых объектах, которые имеют вид рекуррентных формул
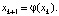(1)
При этом φ называют отображением и говорят, что (1) определяет дискретную динамическую систему [1–3]. В общем случае φ может быть непрерывной, разрывной, монотонно возрастающей или убывающей, иметь точку максимума. Ясно, что если задать начальную точку x0, то, используя формулу (1), можно построить последовательность
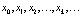(2)
Числовая последовательность, построенная по такому принципу, называется итерационной. При этом (2) называют также решением, а соответствующее множество точек на оси 0x –траекторией динамической системы (1), выпущенной из точки x0. Может так случиться, что последовательность (2), индуцируемая некоторой функцией φ, будет иметь вид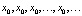 
В этом случае говорят о точке покоя системы (1) и о решении x = x0 уравнения x = φ(x). Если числа в последовательности (2) начинают периодически повторяться, например 
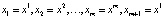, то говорят о периодическом решении (или траектории). При этом число m называют периодом решения (соответственно траектории). Обратим внимание, что простейшие примеры рекуррентных формул вида (1) изучаются ещё в средней школе. Это хорошо знакомая из курса математики арифметическая прогрессия, задаваемая формулой φ(xk) = xk + d, здесь d – заданное число, называемое разностью, и геометрическая прогрессия, определяемая формулой φ(xk) = xk∙q, здесь q – число, называемое знаменателем. Конечно, простота поведения последовательностей, отвечающих этим математическим моделям, обусловлена простотой функций φ, а именно их линейностью. Более содержательный пример приводится в стандартном курсе высшей математики и связан с алгоритмом вычисления квадратного корня из числа a: пусть 
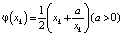. Тогда соответствующая этому отображению последовательность (2) при 
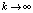будет иметь предел. Доказывается, что этим пределом будет число 
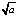, причем этот корень можно вычислить с любой степенью точности.
Заметим, что исторически дискретные модели в математике, по всей видимости, начали появляться ещё в XIII в. Это, в частности, знаменитая последовательность Фибоначчи [4]. Существенно позднее такие объекты изучались в связи с численным решением алгебраических и трансцендентных уравнений вида f(x) = 0 [5, 6]. Здесь речь идет о методе касательных (Ньютона), для которого при определенных условиях на функцию f рекуррентная формула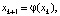 
где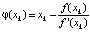 
, позволяла найти корень уравнения f(x) = 0 с любой степенью точности; методе хорд 
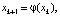где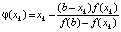 
; простых итераций 
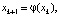где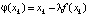 
и др. Некоторые из этих методов сегодня излагаются во втузах, в связи с численным решением уравнения f(x) = 0. Позднее обнаружилось, что численное решение обыкновенных дифференциальных уравнений, например, по методу Эйлера, также сводится к вычислениям по подобным формулам [6, 7]. Кроме того, одним из эффективных современных инструментов численного исследования многомерных динамических систем является итерационный метод точечных отображений, восходящий к А. Пуанкаре [8].
Во второй половине XX в. в центр внимания ученых попали математические модели, также имеющие простую структуру вида (1), которые для некоторых φ демонстрировали весьма сложное поведение траекторий, названное впоследствии детерминированным хаосом.
Целью настоящей статьи является краткое адаптированное для студентов первого курса втуза (с небольшим количеством учебных часов) изложение одной динамической системы, именуемой в литературе сдвигом Бернулли. Предлагается этим материалом завершить тему «Численное решение конечных уравнений» курса математического анализа. Ранее подобная связка этих учебных вопросов не предлагалась. На наш взгляд, такая последовательность изложения возможна и целесообразна, так как отвечает на вопрос студенческой аудитории: «А что будет, если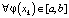 
, а числовая последовательность итераций (2) предела не имеет?» Ответ же на этот вопрос, как оказалось, нетривиален и послужил началом новой бурно развивающейся сегодня науки – нелинейной динамики, изучающей нелинейные модели, бифуркации, детерминированный хаос, фракталы [9, 10]. О проблемах модернизации курса математики в последнее время много говорится на конференциях, а также на страницах журнальной и монографической литературы (например, [11–13]). На наш взгляд, включение предлагаемого материала в учебную программу позволит частично заполнить существующую брешь между устоявшимся классическим втузовским курсом математики и новым научным направлением – детерминированным хаосом.
Отображение сдвиг Бернулли
Конкретизируем теперь систему
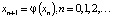
полагая, что φ имеет вид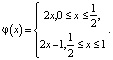 
График φ в этом случае будет разрывным и представлен на рис. 1 [3, 9].
Здесь, как нетрудно видеть, условие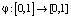 
выполнено и траектория, выпущенная из произвольной начальной точки 
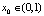, целиком находится в интервале (0,1). При этом положений равновесия в интервале (0,1) у системы нет. Заметим, что модель можно задать кратко 
.
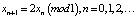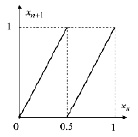
Рис. 1. График отображения φ(x)
Далее для того, чтобы выявить особенности в поведении траекторий такой системы, будем записывать ее члены не в десятичном, а в двоичном виде. На наш взгляд, переход к двоичной системе полезен и актуален в связи с цифровизацией многих технических дисциплин.
Пусть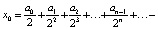 
начальная точка. Здесь числа ai принимают лишь два значения: 0 или 1. Число x0 будем при этом записывать, как обычно, в виде 
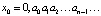. Попутно заметим, что если все числа ai = 0, то x0 = 0; если все ai = 1, то x0 = 1. Если число a0 = 1, то 
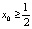, если 
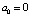, то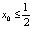 
.
Вычислим последовательно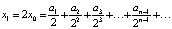 
;
; 
.
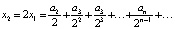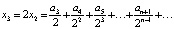Легко видеть, что на n-м шаге будем иметь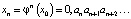 
. Это свойство и оправдывает термин «сдвиг». Число xn+1 получается из xn путем сдвига двоичного набора цифр числа xn влево, при этом цифра первого его двоичного разряда (0 или 1) исчезает.
Рассмотрим теперь две близкие начальные точк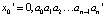и:
… и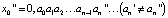 
и соответствующие траектори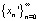и 
и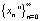 
. Очевидно, что разность 
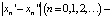представляет собой монотонно возрастающую числовую последовательность, при этом 
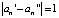. Таким образом, если два начальных числа 
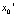и 
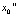отличаются в n + 1 знаке после двоичной запятой, то числа 
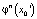и 
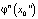отличаются уже в первом знаке. При этом точк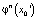и 
и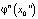 
оказываются в разных промежутках 
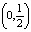и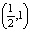 
. Это свойство траекторий называется чувствительной зависимостью от начальных данных и присуще всем динамическим системам с хаотическим поведением.
Рассмотрим теперь случай, когда x0 – рациональное число. Здесь есть две возможности: либо число x0 представляется конечной двоичной дробью, либо – двоичной периодической.
В случае конечной дроби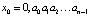 
ясно, что 
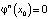и траектория, заканчивает эволюцию в положении равновесия x = 0. В случае периодической дроби 
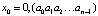, будем иметь 
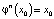. Последнее означает, что x0 является элементом цикла (периодической точкой траектории), при этом n – период цикла. Из проведенных рассуждений следует, что множество периодических траекторий в нашей системе бесконечно, но счетно. Это следует из того, что множество рациональных числе отрезка [0,1] счетно. Однако все периодические траектории неустойчивы, в силу чувствительной зависимости от начальных данных.
Пример 1. Цикл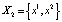 
периода 2 единственный: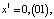 
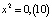. В десятичной форме записи числа x1 и x2 запишутся так
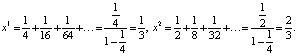
На рис. 2 изображены графики функции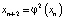 
и биссектрисы 
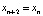. Абсциссы точек пересечения x1 и x2 этих графиков как раз и образуют цикл 
.
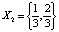Заметим, что в школе и вузовском курсе математики задаче построения графиков функций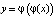 
, 
,…, 
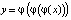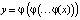внимания уделяется мало. Желательно на практике восполнить этот пробел, ибо эта задача в настоящее время является актуальной.
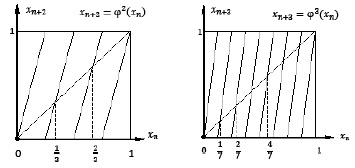
Рис. 2. График второй итерации Рис. 3. График третьей итерации
Рассмотрим теперь цикл периода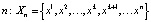 
.
Здесь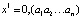 
, 
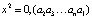,…, т.е. цифры числа 
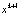представляют собой круговую перестановку цифр числа xk: 
.
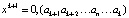Выведем полезную формулу перехода от двоичной записи числа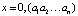 
к десятичной. Для этого представим x в виде
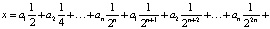
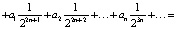
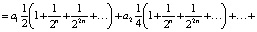
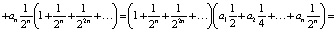
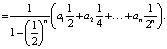
Откуда вытекает формула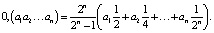 
Пример 2. Существует два цикла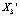 
и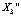 
периода 3 (рис. 3):
1. 
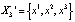, здесь 
, 
, 
.
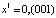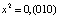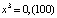Или в десятичной записи: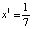 
, 
, 
.
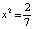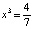2. 
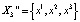, здесь 
, 
, 
.
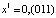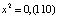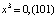Или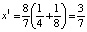 
, 
, 
.
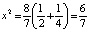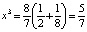Пример 3. Существуют три цикла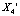 
, 
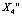и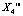 
с периодом 4
1. 
,
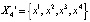где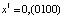 
, 
, 
, 
.
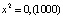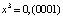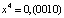Или в десятичной записи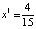 
, 
, 
, 
.
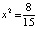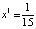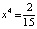2. 
,
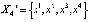где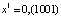 
, 
, 
, 
.
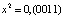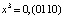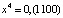Или в десятичной записи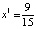 
, 
, 
, 
.
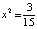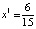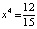3. 
,
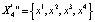где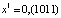 
, 
, 
, 
.
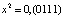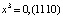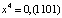Или в десятичной записи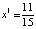 
, 
, 
, 
.
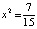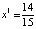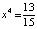Справедливо следующее простое утверждение.
Теорема 1. Если n > 1 простое число, то число циклов периода n будет равно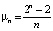 
.
Речь идет о циклах с наименьшим периодом.
Если же число n – не простое, то вопрос о количестве циклов является нетривиальным.
Пусть X – множество корней уравнения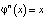 
. Обозначим 
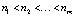– делители числа n (n1 = 1, nm – максимальный делитель), Xn – множество периодических точек периода n 
, 
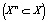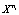– множество периодических точек периода 
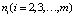. Тогда справедлива следующая теорема.
Теорема 2. Для числа периодических точек Xn и количества циклов μn периода n справедливы формулы: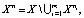 
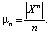
Результаты подсчета количества циклов периода n приведены в таблице.
Циклы периода n
|
Период цикла n |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Количество циклов μn |
1 |
2 |
3 |
6 |
9 |
18 |
30 |
56 |
99 |
186 |
335 |
Дальнейшие вычисления величин μn(n > 12) приводят к приближенной формуле:
,
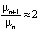точность, которой с ростом n возрастает. Грубо говоря, количество циклов μn с периодом n при больших значениях n растет геометрически.
Пусть теперь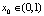 
произвольное иррациональное число. Напомним, что в иррациональном числе любая последовательность из k цифр повторяется бесконечное число раз.
Для определенности представим x0 в виде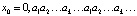 
Тогда для заданного сколь угодно малого произвольного числа ε > 0 найдется натуральное число m = m(ε), такое, что 
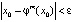, т.е. траектория, выпущенная из начальной точки x0, через некоторое время (через некоторое количество итерационных шагов) возвращается в ε – окрестность Sε(x0) точки x0. Это свойство траекторий называется эргодичностью [9].
Замечание
Рассмотренный в настоящей статье пример допускает обобщение. Подобным образом можно было бы рассмотреть системы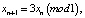 
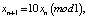n = 0, 1, 2,... или 
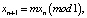n = 0, 1, 2,... (m – целое). Другие примеры систем со сложным поведением траекторий можно найти, например, в работах [3, 9, 14]).
Заключение
Известно, что рабочие программы курсов математического анализа технических вузов включают изучение методов (способов) приближенного решения алгебраических и трансцендентных уравнений вид f(x) = 0. Здесь имеются в виду методы Ньютона, хорд, простых итераций и др. Суть всех сводится к построению некоторых итерационных процедур, позволяющих приближенно находить корень уравнения f(x) = 0 с любой наперед заданной степенью точности. При этом корень изначально локализован в некотором интервале (a, b). Основаны эти способы на построении в окрестности (a, b) некоторой вспомогательной функции φ, итерации которой сходят к корню. Однако, как оказалось, итерационные процессы, построенные по рекуррентной формуле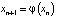 
, 
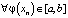, интересны сами по себе, вне связи с задачей о решении уравнения f(x) = 0. Причем в настоящее время известен весьма широкий класс функций φ, для которых индуцируемая итерациями последовательность xn ведет себя очень сложно. В этом случае говорят, что φ порождает хаотическую динамику или детерминированный хаос. Этот класс систем хорошо изучен, описан в научной литературе и уже построена достаточно полная теория. В настоящей статье мы выбрали простейший из таких примеров и считаем, что в курсе математического анализа знакомство студентов с таким сложным поведением итераций в таких системах должно найти отражение. К тому же это не займет много учебного времени, познавательный эффект будет очевидным, а сложность материала вполне по силам студенту-первокурснику.