Современная система образования в России направлена на формирование личности как основной социальной ценности: способной адаптироваться к изменениям в обществе, активно включаться в профессиональную деятельность и подстраиваться к новым условиям, быстро и самостоятельно обучаться новому. Готовность к осуществлению такого обучения влечет за собой необходимость изменения и подхода к подготовке будущих педагогов в вузе. Традиционная система обучения была направлена на освоение готового знания, что не требовало от студента включения различных видов мышления и проявления активности при решении проблем, а наоборот, ограничивало круг рассматриваемых явлений при изучении различных дисциплин. Сегодня система образования обновляется в сторону активной позиции студента в ходе обучения, формирования разносторонней личности будущего профессионала, творческой и исследовательской деятельностей, а также развития социально значимых качеств, которые потребуются человеку как для выполнения профессиональных обязанностей, так и в повседневной жизни.
Нацеленность современного образования на развитие профессиональных компетенций обусловливает необходимость внедрения в процесс обучения таких подходов, методов и технологий, которые позволяют учитывать запросы общества и рынка труда. Анализ различных подходов к обучению показывает, что построение учебного процесса в рамках интегрированного обучения позволяет формировать необходимые компетенции будущего педагога, способного проявлять профессиональные качества на высоком уровне. Технология интегрированного обучения позволяет создавать целостное представление об окружающей (современной) действительности и создает возможность формирования общей платформы для сближения предметных знаний. Важность и необходимость этого следует из государственного образовательного стандарта, где прописаны, например, такие требования к будущему специалисту, как обладание целостным представлением об образовании – особой сферы социокультурной практики, владение системой знаний о человеке как личности и индивидуальности, способность к проектной и исследовательской деятельности.
Целью данного исследования является теоретическое обоснование необходимости интеграции знаний при подготовке будущих учителей-предметников (в области математики); определение методов и средств качественной подготовки учителя математики в вузе на основе принципа интегративности.
Материалы и методы исследования
Профессиональная подготовка в вузе направлена на формирование теоретических знаний и практических умений, а также компетенций при освоении студентами различных учебных курсов и дисциплин. Важно комплексно использовать изученный теоретический материал при решении разного рода проблем и увидеть точки его соприкосновения с разными науками, что позволит в будущем эффективно и быстро решать как социальные, так и профессиональные задачи. Заметим, что каждую профессиональную задачу рассматривают как междисциплинарную или интегративную, так как ее решение всегда требует всестороннего анализа, поиска путей и средств решения, привлекая для этого знания и методы из различных областей знаний. Это означает, что для подготовки студента к осуществлению творческой профессиональной деятельности в качестве учителя математики и формированию соответствующих профессиональных и личностных компетенций можно применить технологию интегрированного обучения.
Ученые предлагают различные подходы к реализации интегрированного обучения для подготовки специалистов. Первый путь направлен на создание и применение интегративных курсов, а также интеграцию предметных областей и их составляющих – знаний, умений, компетенций (Н.П. Коваленко, А.Л. Чекин, Максимова Л.И., Машарова Т.В., Щенникова С.В.) [1, 2]. Второй подход связан с понятием «практический синтез», понимаемый авторами как соединение и использование разнообразных приемов, методов, путей и технологий обучения, которые показали свою эффективность на практике (Ю.С. Бродский, В.Д. Семенов и др.).
Если говорить о математическом образовании, есть исследования, в которых предлагается использование профессиональных и прикладных задач, для решения которых используется метод математического моделирования [3]. Можно говорить, что в основном в них разрабатываются теоретические вопросы интеграции в образовании, но недостаточно исследований, касающихся практической реализации данной технологии при подготовке будущих учителей математики.
Математику как учебный предмет длительное время рассматривали в качестве инструментария, технологии для изучения других дисциплин, и, как следствие, ее содержание постепенно стало носить лишь научный характер, а точнее, теоретизированный. Обучение математике стало переходить на формальный уровень: изучение формул, определений, теорем. Стали забывать о практической направленности и неограниченных возможностях математики, которые позволяют формировать духовную культуру личности, позволяют показать связь математики с жизнью, всю красоту математических знаний. Часто при обучении математическим дисциплинам, особенно в вузе, уделяется внимание усвоению конкретных теоретических фактов и при этом не рассматривается область их практического применения в различных областях знаний, профессиональной и повседневной жизни человека, история их возникновения и развития. Это приводит к снижению уровня интереса к изучению математических дисциплин у обучающихся, которые считают их самыми абстрактными и сложными среди изучаемых наук.
Поэтому важным вопросом, который требует своего решения, является интеграция математического содержания как внутри предмета, так и с другими областями знаний, что позволит легче выстраивать процесс обучения с целью развития профессиональной компетентности учителя математики. В процесс подготовки учителя-предметника важно включить общекультурную составляющую математического содержания, чтобы показать важность математических знаний для описания явлений действительности, в повседневной жизни и различных направлениях профессиональной деятельности человека. Общекультурная составляющая связана с установлением взаимосвязей математики с искусством, религией, законами живой природы и другими науками, что и является основой интегративного подхода.
В ходе исследования были выделены возможные пути практической интеграции знаний при обучении математическим дисциплинам: интегративные курсы; интегративные (комплексные) задания; реализация исторической линии в обучении разным математическим дисциплинам; организация исследовательской деятельности (портфолио, проекты, курсовые работы и ВКР).
Под интегративным подходом в образовании будем понимать «взаимодействие субъектов образовательного процесса, которое направлено на организацию поисковой деятельности студентов, а затем ее осуществление через активное и самостоятельное приобретение ими знаний, овладение необходимыми умениями в условиях их внутридисциплинарного и междисциплинарного синтеза; а также позволяющее обеспечить индивидуальное профессиональное творческое становление будущего педагога» [3].
Интеграция в широком смысле предполагает установление взаимосвязей между содержанием различных областей знаний, когда некая проблема или явление рассматривается с разных сторон, привлекая для этого знания из различных учебных предметов, а также показывая необходимость изучения нового теоретического материала, а также поиска или конструирования методов решения проблемы. Включение обучающихся в такой процесс обучения позволяет повышать уровень обучения до научного, показывать необходимость знаний по различным учебным предметам для описания явлений окружающего нас мира, устанавливая при этом естественные взаимосвязи между областями знаний. Отметим, что это способствует и развитию качеств личности обучающихся, мышления, умения анализировать, обобщать и делать выводы, искать рациональные пути решения проблем, привлекая для этого все имеющиеся возможности и знания.
Если говорить об интеграции математического содержания, то нужно отметить, что возможны два пути: внутридисциплинарная и междисциплинарная интеграция. Внутридисциплинарная предполагает установление взаимосвязей разных разделов одной предметной области математики, когда некая проблема (задача) решается с привлечением знаний и из алгебры, и из геометрии, и из математического анализа и т.д. Междисциплинарная интеграция предполагает решение проблемы с привлечением не только математических знаний, но и знаний из других учебных предметов и областей знаний.
Подходы к построению интегративного содержания в вузе могут быть различны, но наиболее эффективным и доступным, на наш взгляд, является включение интегративных курсов, которые дают большую свободу преподавателю для выбора содержания и методов обучения. Интегративным курсом по математике будем называть учебный курс, который: включает более широкое математическое содержание (по сравнению с прописанным в стандарте); позволяет устанавливать различные связи математики как внутридисциплинарного, так и междисциплинарного характера; учитывает профессиональный и общекультурный характер достижения образовательных результатов.
Для студентов педагогических направлений института математического моделирования и игропрактики ПсковГУ разработаны курсы по выбору, которые включают элементы интегративного подхода: «Математика и гармония окружающего мира», «Принцип симметрии и его универсальное значение», «Золотая пропорция», «Компетентностные задачи по геометрии». Содержание курса «Математика и гармония окружающего мира» раскрывает взаимосвязи математики и таких областей искусства, как архитектура, живопись и музыка. Содержание следующих двух курсов выстраивается вокруг таких математических понятий, как симметрия и пропорция, с которыми человек часто встречается в жизни и при изучении других дисциплин. Дополнительным материалом, который включен в содержание курсов, являются новые достижения науки XX в. Так, например, различные проявления симметрии и её категорий (асимметрия и диссимметрия) в науке, природе, искусстве; открытия Б.В. Раушенбаха в области изобразительного искусства, «переоткрытие» золотой пропорции и др.
В ходе реализации данных курсов студенты выполняют различные интегративные задания. Ниже приведены примеры интегративных заданий, в которых раскрывается взаимосвязь математики с архитектурой:
1. На одном из фасадов здания можно увидеть рисунок в виде стрельчатой арки (рис. 1), в которую вписана окружность и две равные полуокружности. АВ = 20 м. По чертежу восстановите способ построения рисунка, выделите главную вычислительную задачу построения и решите ее.
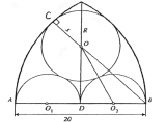
Рис. 1. Стрельчатая арка

Рис. 2. Церковь Спаса на Ильине улице в Новгороде
2. Рассчитайте приблизительный внутренний объем церкви Спаса на Ильине улице в Новгороде без учета апсиды и главы. План храма представляет собой квадрат со стороной 24 м, высота храма по центру фасада – 24 м, по краям – 16 м (рис. 2).
Курс «Компетентностные задачи по геометрии» построен на интеграции знаний школьной геометрии и вузовского курса методики обучения математике. Также изучаются основы компетентностного подхода, что важно для будущего учителя. Изучение данного курса способствует развитию профессиональной компетентности, как предметной, так и методической ее составляющих. Курс содержит интегративные задания, которые требуют математических, методических, межпредметных, практических знаний. Выполнение таких заданий требует творческого и исследовательского подходов.
Пример задания: Решить задачу и выполнить задания.
Задача. Древние русские города были защищены от врагов каменными оборонительными укреплениями. Каменные крепости имели высокие толстые стены и башни, которые использовались жителями при отражении нападений. Осады таких крепостей могли длиться месяцами, и для выхода за пределы стен могли иметься тайные выходы, которые часто называли «вылазами». В исторических документах имеются сведения, что в одной из таких башен (рис. 3, башня справа) имелся глубокий колодец шириной 3,5 фута. Представим, что на дне этого колодца и был такой «вылаз», через который доставлялось продовольствие и информация. В настоящее время принято решение засыпать колодец сухим песком, что защитит башню от влаги и разрушения. Колодец достаточно глубокий, спускаться в него опасно из-за обрушения стен. Песок будет доставлять грузовая машина, которая за один раз может привезти 5 т песка. Сколько таких машин песка потребуется заказать, чтобы засыпать колодец полностью (на половину; на три четверти), если при бросании в колодец груза (массой 0,3 кг) мы услышим звук его удара о землю через 1 секунду;2 секунды; если известно, что глубина колодца 16,5 футов?

Рис. 3. Башни псковского Кремля
Задания: 1. Докажите, что задача является компетентностной.
2. Пропишите этапы работы над данной задачей.
3. Выделите знания, необходимые для решения данной задачи: 3.1. математические, 3.2. межпредметные, 3.3. практические (связанные с повседневной жизнью, профессиональными видами деятельности человека).
4. Напишите фрагмент конспекта урока по работе с этой задачей на уроке.
Еще одним направлением интеграции математического содержания служит реализация исторической линии при обучении различным математическим дисциплинам.
Несмотря на то, что принцип историзма признавался одним из общепринятых средств повышения качества математического образования, к сожалению, по сей день теоретические исследования в рассматриваемом направлении существенно опережают практику их внедрения, несмотря на то, что новые федеральные стандарты уже сейчас ориентируют нас на актуализацию историко-математической составляющей в обучении. Часто учителя математики не обладают достаточным уровнем методических знаний и умений по систематическому, плодотворному использованию принципа историзма в учебном процессе, а зачастую показывают низкий уровень историко-математической подготовки. Несомненно, что первоначальный опыт по систематическому включению исторической составляющей в процесс обучения математике будущие учителя должны приобретать еще в период обучения в вузе, ориентируясь на соответствующий стиль работы своих преподавателей.
Предлагаем следующие направления реализации исторической линии при изучении различных математических дисциплин.
1) Включение преподавателями теоретических сведений из истории математики, а также историко-математических заданий при изучении различных математических дисциплин начиная с первого курса.
Ниже приведены примеры интегративных историко-математических заданий по дисциплине «Аналитическая геометрия».
Пример 1. Лекция по аналитической геометрии «Культурно-исторический экскурс».
На первой лекции студентам рассказывается об истории развития геометрической линии в математике, упоминаются имена геометров, которые внесли существенный вклад в развитие геометрии. Отдельный акцент делается на формировании разделов геометрии: аналитической геометрии, дифференциальной геометрии, неевклидовой геометрии, основания геометрии и др. в историческом контексте.
После лекции студентам предлагаются вопросы-задания:
1. Что в переводе с греческого означает термин «геометрия»? С чем связано это название? Запишите эти сведения в тетрадь.
2. Какие имена древнегреческих математиков вы знаете? Выберите трех из них и кратко опишите их достижения в математике.
3. Кого можно считать основателем аналитической геометрии? Какая дата считается датой возникновения аналитической геометрии и почему?
4. На «стыке» каких математических дисциплин возникла аналитическая геометрия? Приведите примеры других разделов геометрии, которые возникли на стыке некоторых математических дисциплин.
5. Что вас больше всего заинтересовало в лекции? Запишите свои мысли, как если бы вы кому-то рассказывали об этом.
Пример 2. Лекция по аналитической геометрии «Системы координат на плоскости».
На лекции студентов знакомят с различными системами координат на плоскости: аффинной, прямоугольной декартовой, полярной. Так же изучаются формулы связи координат в различных системах: прямоугольной, декартовой и полярной. В курсе математического анализа при изучении темы «Функция» рассматривается вопрос о задании функций уравнениями в полярной системе координат. На данном занятии можно предложить интегративные задания для установления связи при изучении этой темы в аналитической геометрии и математическом анализе.
Вопросы-задания:
1. Что вам известно о происхождении полярной системы координат? Запишите эти сведения в тетрадь.
2. Постройте уравнения некоторых кривых в полярных координатах: спираль Архимеда, полярная роза и др.
3. Самостоятельно изучите вопрос трехмерного расширения полярной системы координат в трехмерном пространстве: цилиндрическая и сферическая системы координат. Кратко изложите эти сведения в тетради.
4. Найдите примеры применения рассмотренных систем координат в практической деятельности человека. Запишите эту информацию, как если бы вы кому-то рассказывали об этом.
Такие задания позволяют сделать студента соучастником познания, задействуют личностный опыт. При выполнении ряда заданий участник должен самостоятельно отобрать необходимый материал, выразить свое отношение к нему и изложить так, как если бы он кому-то это рассказывал. Данная деятельность приводит к формированию метазнаний, которые являются кирпичиками, составляющими ядро знаний. В случае успешного выполнения заданий новым опытом студенты делятся с другими обучающимися, осуществляется коммуникация. Приобретенный опыт осмысливается, на основании рефлексии анализируется и корректируется. Наконец, ставятся новые задачи, полученные компетенции применяются в новых незнакомых ситуациях.
2) Формирование историко-математического портфолио студентами при изучении различных математических дисциплин. Выполнение исследовательских работ.
Портфолио студенты формируют на протяжении всего периода обучения при изучении различных математических дисциплин. Целью портфолио является накопление историко-математических сведений для работы будущего учителя математики. Рубрики портфолио: этимология понятий, историко-математические задачи, личности в истории математики, методические разработки. Студенты могут предложить свои рубрики и дополнить ими портфолио. Результаты работы над портфолио можно включать в итоговую аттестацию.
3) Проведение студентами интегрированных историко-математических уроков в рамках курса «История математики».
Студентам предлагается для проведения уроков список тем, например: «Математические представления в Древнем Египте», «Математические представления в Древнем Вавилоне», «Фалес Милетский, его математические воззрения», «Пифагор Самосский, его вклад в становление математики» и др. Роль учащихся школы выполняют студенты группы. Урок должен состоять из трех частей: теоретической, практической и диагностической. Теоретическая часть урока предполагает изложение студентом нового материала по теме; практическая – разбор примеров практических заданий, которые связаны со школьной программой или расширяют и дополняют ее; диагностическая – составление студентом-педагогом диагностических материалов в виде вопросов, теста или кроссворда, которые проверяют качество усвоения пройденного материала. Результаты таких заданий проверяются выступающим, выставляются баллы.
В конце изучения курса «История математики» был проведен опрос студентов, который показал, что такая практика проведения уроков интересна студентам. Особенно понравилась организация практической части, когда необходимо было не только изложить информацию, но и проявить педагогическое мастерство – организовать решение задания, организовать работу у доски, контролировать процесс обучения, провести оценку знаний.
4) Знакомство с историей родного края через решение математических задач в курсе «Элементарная математика».
Для студентов второго курса для систематизации знаний по разделу «Уравнения и неравенства» и повторения методов решения различных видов уравнений была разработана серия занятий, построенных на знакомстве с историей родного края. В качестве исторического материала была выбрана тема «Великая Отечественная война в городе Дно». Дно – это небольшой город Псковской области, который при этом является крупной железнодорожной станцией.
Каждое занятие было направлено на повторение конкретного вида уравнений и неравенств, и при этом строилось на знакомстве с историческими сведениями по конкретному событию или периоду во время войны. Например, знакомство с г. Дно, его особенностями, географическим положением происходило при повторении темы «Алгебраические уравнения и неравенства». Преподаватель знакомит обучающихся с историческими сведениями, одновременно с этим информация с математическими заданиями по теме появляется на слайдах. Например, чтобы узнать численность населения города до начала войны, число железнодорожных направлений и другие сведения, студентом нужно выполнить задания. Примеры заданий представлены в статье [4].
Такие интегративные задания вызывают интерес у студентов, они активно включаются в процесс обучения, знакомятся с методами работы, самостоятельно готовы создавать такие занятия и задания и применять технологию интегрированного обучения в своей будущей профессиональной деятельности.
Сегодня многие исследователи изучают возможности формирования профессиональных качеств студентов в рамках интегративного подхода [5, 6].
Заключение
В статье обоснована необходимость построения образовательного процесса в вузе в рамках интегративного подхода. Выделены возможные пути практической интеграции знаний при обучении математическим дисциплинам, которые реализуются преподавателями института математического моделирования и игропрактики ПсковГУ. Приведены примеры интегративных заданий, предлагаемых в рамках интегративных курсов и отдельных дисциплин. Раскрыта роль исторической линии в обучении разным математическим дисциплинам, выделены направления ее реализации в вузе.



