Современные гаджеты делают жизнь человека более комфортной, а также расширяют возможности. А неотъемлемым этапом производства дискретных объектов (цифровых плат, блоков, модулей) является этап выходного контроля. Этот этап определяет исправность объекта, при необходимости обнаруживаются и устраняются дефекты, которые возникли. И поэтому от того, насколько быстро и качественно будут выполняться операции по диагностированию объектов, зависит стоимость изделия.
Согласно ГОСТ 20911-89 «Техническая диагностика. Термины и определения» техническая диагностика – это область знаний, охватывающая теорию, методы и средства определения технического состояния объектов диагностирования (ОД). В частности, при диагностировании средств вычислительной техники используются принципы построения и организации ЭВМ. Одним из направлений эволюции ЭВМ является распараллеливание процессов на различных уровнях иерархии как средство повышения быстродействия [1]. Краткая история параллелизма в ЭВМ изложена в [2].
Распараллеливание процессов – одно из направлений технической диагностики, обеспечивающее снижение временных затрат.
Параллельное, конвейерное и поточное диагностирование дискретных объектов [3, 4] базируется на применении алгоритмов, которые не только повышают быстродействие систем диагностирования, но и обеспечивают существенное снижение степени зависимости времени диагностирования различных объектов друг от друга.
Для дискретных объектов диагностирования характерно тестовое диагностирование, при котором на объекте подаются специальные, так называемые тестовые воздействия. Тестовые воздействия и последовательность их выполнения называются тестом [5].
В работе [6] рассмотрено множество алгоритмов параллельного диагностирования дискретных объектов. Элементами множества являются алгоритмы-процедуры, такие как:
– параллельная процедура с повторными запусками теста;
– параллельная процедура с продолжением теста;
– параллельная процедура с неполными возвратами теста;
– ν-процедура;
– ν-процедура с неполными возвратами теста и другие.
Процедуры диагностирования и представляют собой то множество объектов, элементы которого анализируются с точки зрения СВЗ. Каждая процедура описывается аналитическим выражением для вычисления СВЗ, в частности для параллельной и n-процедуры эти формулы имеют следующий вид:
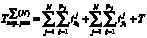
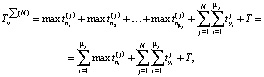(1)
где N – количество параллельно диагностируемых дискретных объектов; T – длина теста;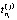 
– время поиска i-го дефекта в j-м объекте; 
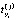– время устранения i-го дефекта в j-м объекте; μj – количество дефектов в j-м объекте; max 
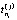– максимальное время поиска i-го дефекта среди всех i-х дефектов N объектов, и находится этот дефект в j-м объекте [6].
В работе [6] доказано, что каждая из процедур позволяет повысить быстродействие процесса диагностирования группы однотипных дискретных объектов.
Целью настоящего исследования описания нового оптимального алгоритма, который является эффективным по сравнению с параллельным алгоритмом диагностирования и ν-процедуры диагностирования дискретных объектов.
Предположим, что новый оптимальный алгоритм дает возможность сокращения суммарных временных затрат на обнаружение дефектов за счёт оптимизации процесса параллельного тестирования множества ДО. Согласно оптимизации диагностических процедур (1) допустим, что существует тест T, обнаруживающий все возможные дефекты, составляющие множество дефектов di∈[0,D] некоторого дискретного объекта (ДО).
Рассмотрим пример параллельного диагностирования трёх (N = 3) однотипных ДО, в каждом из которых имеются дефекты: в первом – один дефект (µ1 = 1), во втором – два дефекта (µ2 = 2), в третьем – три дефекта (µ3 = 3). Длина теста T = 30 условных временных единиц (уве), t0 – начальный тестовый вектор, tk – конечный тестовый вектор.
Пусть моменты обнаружения дефектов в трёх диагностируемых объектах распределены на всей длине теста так, как показано на рис. 1, а, то есть время (момент) обнаружения первого дефекта во втором объекте t(2)1 = 16 (уве), время обнаружения первого дефекта в третьем объекте t(3)1 = 18 (уве), время обнаружения второго дефекта во втором объекте t(2)2 = 20 (уве), время обнаружения первого дефекта в первом объекте t(1)1 = 22 (уве), время обнаружения второго дефекта в третьем объекте t(3)2 = 26 (уве), время обнаружения третьего дефекта в третьем объекте t(3)3 = 28 (уве).
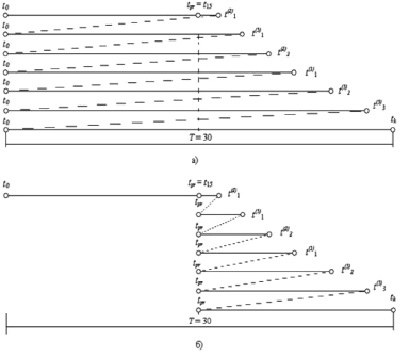
Рис. 1. Временные диаграммы алгоритмов диагностирования для трех ДО (N = 3), содержащих шесть дефектов (μ = μ1 + μ2 + μ3 = 6): а) параллельного диагностирования; б) оптимального параллельного диагностирования
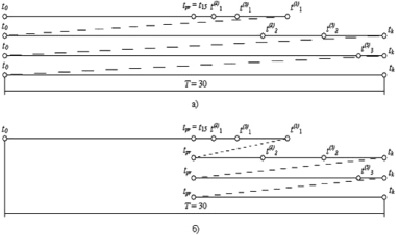
Рис. 2. Временная диаграмма диагностирования для трёх ДО (N = 3), содержащих шесть дефектов (μ = μ1 + μ2 + μ3 = 6): а) с использованием алгоритма n-процедуры; б) оптимального диагностирования с использованием алгоритма n-процедуры
В соответствии с [4, 6] временные диаграммы параллельного диагностирования и диагностирования с использованием алгоритма n-процедуры будут выглядеть, как показано на рис. 1, а, и рис. 2, а.
При параллельном диагностировании, рис. 1, а, тест подаётся параллельно во все N диагностируемых объектов, выходные сигналы с идентичных выходов сравниваются между собой и на основании вычисления мажоритарной функции неравнозначности определяется неисправный ОД. После устранения обнаруженного дефекта тест реверсируется в начальное состояние t0 и повторяется снова до обнаружения следующего дефекта и так продолжается до тех пор, пока не будут обнаружены и устранены все дефекты, о чём свидетельствует полный прогон теста из начального состояния t0 в конечное tk.
При этом всё множество диагностируемых объектов заменяется одним, виртуальным, содержащим все дефекты всех N ОД.
Пунктиром на рисунках показан процесс реверсирования теста в начальное t0 или некоторое промежуточное состояние tpr. Так как на практике это осуществляется не последовательным перебором тестовых векторов в обратном порядке, а сбросом, то время реверса теста в расчётах принимается равным нулю.
Тогда в соответствии с (1) суммарные временные затраты на параллельное диагностирование трёх ДО, содержащих шесть дефектов (μ = μ1 + μ2 + μ3 = 6), определяются с помощью выражения
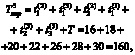(2)
где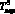 
– суммарные временные затраты на обнаружение всех дефектов трёх ДО (N = 3) при параллельном диагностировании.
При диагностировании с использованием алгоритма n-процедуры [6], рис. 2, а, тест также параллельно подаётся во все диагностируемые объекты, но при обнаружении первого дефекта, в данном случае это первый дефект во втором ОД, время обнаружения которого t(2)1, объект, в котором обнаружен дефект, исключается из пространства поиска, тест продолжается до тех пор, пока не будет обнаружен другой дефект. В рассматриваемом примере это первый дефект в третьем объекте, время обнаружения которого t(3)1, этот третий объект также исключается из пространства поиска, и тест продолжается до тех пор, пока не будет обнаружен следующий первый дефект в одном из оставшихся объектов, а это первый дефект в первом объекте, время обнаружения которого t(1)1.
Только после этого все «первые» дефекты устраняются, тест реверсируется в начальное состояние и повторяется.
Таким образом, при первом прогоне теста обнаруживаются все «первые» дефекты, при втором прогоне теста – все «вторые» и т.д. При этом суммарное время обнаружения «первых» дефектов заменяется одним максимальным среди них. Для данного примера это
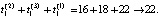
В рассматриваемом примере максимальное время обнаружения и «вторых», и «третьих» дефектов вырождается в T (это самый неблагоприятный случай).
Тогда в соответствии с (1) суммарные временные затраты на диагностирование с использованием алгоритма n-процедуры трёх ДО, содержащих шесть дефектов (μ = μ1 + μ2 + μ3 = 6), определяются с помощью выражения
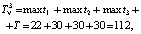(3)
где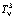 
– суммарные временные затраты на обнаружение всех дефектов трёх ДО (N = 3) при параллельном диагностировании с использованием алгоритма n-процедуры;
maxti – максимальное время обнаружения дефекта среди множества i-х дефектов.
Анализируя временную диаграмму диагностирования трех ДО рассматриваемого примера, рис. 1, а, можно заметить, что она избыточна. В самом деле, первый дефект (в данном случае это первый дефект во втором объекте t(2)1= 16) обнаруживается на шестнадцатом тестовом векторе. Пятнадцать предшествующих тестовых векторов дефектов не обнаруживают. Естественно, что на первом прогоне теста это необходимо в данной ситуации, но при последующих пяти прогонах теста повторять эти пятнадцать тестовых векторов, по-прежнему ничего не обнаруживающих, нецелесообразно.
Аналогичный вывод можно сделать и для временной диаграммы параллельного диагностирования с использованием алгоритма n-процедуры (рис. 2, а).
Чтобы сократить временные затраты на обнаружение дефектов при использовании алгоритмов параллельного диагностирования, предлагается устранить избыточность во временных диаграммах. Предлагается после первого прогона теста его реверсировать не в исходное состояние t0, а в некоторое промежуточное tpr, предшествующее моменту обнаружения первого дефекта, в данном случае это t15.
Следует заметить, что процесс реверсирования теста, как правило, носит скачкообразный характер, то есть тест просто сбрасывается в промежуточное состояние tpr, последовательно, не проходя промежуточные состояния. Поэтому эти временные затраты в вычислениях считаются равными нулю.
На основании изложенного рекомендуется другая временная диаграмма для рассматриваемого примера (рис. 1, б).
Так как тест теперь на каждом повторном прогоне начинается не с исходного t0 положения, а с промежуточного тестового вектора tpr, то суммарные временные затраты на параллельное диагностирование трёх ДО, содержащих шесть дефектов (μ = μ1 + μ2 + μ3 = 6), определяются с помощью выражения
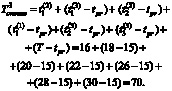(4)
Временная диаграмма оптимального диагностирования с использованием алгоритма n-процедуры для рассматриваемого примера будет выглядеть, как показано на рис. 2, б.
И, соответственно, временные затраты на оптимальное диагностирование с использованием алгоритма n-процедуры трёх ДО, содержащих шесть дефектов (μ = μ1 + μ2 + μ3 = 6), определяются с помощью выражения
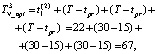(5)
где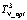 
– суммарные временные затраты на обнаружение всех дефектов трёх ДО (N = 3) при оптимальном диагностировании с использованием алгоритма n-процедуры.
Таким образом, при использовании предложенного оптимального алгоритма параллельного диагностирования шести ДО затрачивается всего 70 условных единиц времени, а при оптимальном диагностировании с использованием алгоритма n-процедуры – 67 условных единиц.
Так как ДО имеет конечное множество состояний, то это позволяет перейти от временных диаграмм к конечным ориентированным графам (рис. 3, а, б).
Вершины графов соответствуют состояниям ОД, в которых происходит обнаружение некоторых дефектов, (то есть i-го дефекта в j-м ДО), а вершины t0 и tk соответствуют начальному t0 и конечному tk состояниям теста и объектов.
Дуги, соединяющие вершины графов, определяют время обнаружения каждого из дефектов t(j)i.
Так как множество возможных значений времен поиска есть конечное множество, мощность которого определяется числом тестовых векторов в тесте T, то можно сказать, что на дугах графа реализуется числовая функция, то есть каждой дуге ставится в соответствие некоторое число t(j)i из конечного множества T.
Пусть на T задан внутренний бинарный ассоциативный закон «+», тогда можно вычислить значение пути через дуги графа.
Для графа рис. 3, а, отображающего параллельное диагностирование, значение пути через дуги графа обозначим Sп:
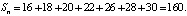(6)
Тогда как для оптимального диагностирования Sopt (рис. 3, б):
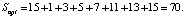(7)
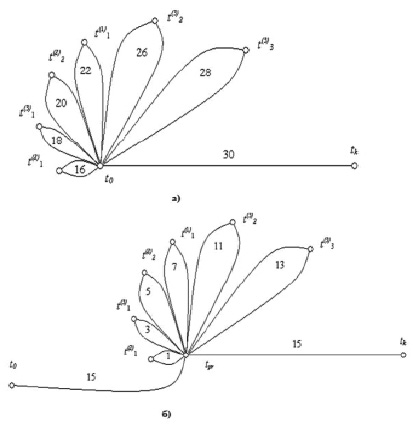
Рис. 3. Графы диагностирования трёх ДО (N = 3), содержащих шесть дефектов (µ = μ1 + μ2 + μ3 = 6): а) параллельного диагностирования; б) оптимального диагностирования
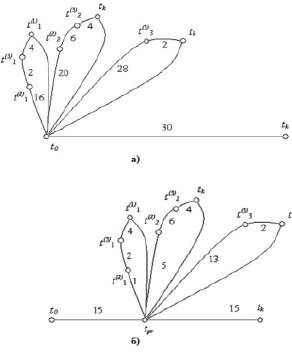
Рис. 4. Граф, отображающий процесс диагностирования для трёх ДО (N = 3), содержащих шесть дефектов (μ = μ1 + μ2 + μ3 = 6): а) с использованием алгоритма n-процедуры; б) оптимального диагностирования с использованием алгоритма n-процедуры трёх
Для графа (рис. 4, а), отображающего диагностирование с использованием алгоритма n-процедуры, значение пути через дуги графа обозначим Sn:
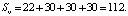(8)
Для графа (рис. 4, б), отображающего оптимальное диагностирование с использованием алгоритма n-процедуры, значение пути через дуги графа обозначим Sn_opt:
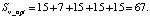(9)
Таким образом, значение пути через дуги графа оптимального диагностирования меньше, чем значение пути через дуги графа параллельного диагностирования:
Sopt < Sп, (10)
Sn_opt < Sn_opt. (11)
Следовательно, очевидны преимущества оптимального диагностирования по сравнению c параллельным и с n-процедурой, а так как числовая функция на дугах графа имеет временную размерность, то можно говорить о быстродействии процесса диагностирования.
Так оптимальное диагностирование в r1 раз быстрее параллельного диагностирования, в r2 раз быстрее диагностирования с использованием n-процедуры
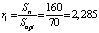, (12)
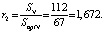(13)
Следовательно, можно сказать, что с увеличением числа диагностируемых объектов и дефектов в них временной выигрыш при использовании оптимального диагностирования будет увеличиваться.
Итак, рассмотрев предложенный новый алгоритм, называемый оптимальным, можно сделать вывод, что он более эффективный по сравнению с параллельным алгоритмом диагностирования и ν-процедуры диагностирования дискретных объектов. И максимальное значение величины выигрыша во времени достигает, когда время перехода теста в промежуточное состояние равно среднему времени обнаружения одного дефекта.