Современному информационному обществу требуется свободная, творческая личность, которая может, получив необходимую информацию, самостоятельно ее проанализировать, сделать выводы и перенести в новые условия, в новое предметное содержание. Для достижения этого необходимо разрабатывать новые педагогические технологии, новые методические подходы на основе развивающего обучения. Одним из таких подходов, с помощью которого обучающиеся смогут самостоятельно находить решения возникших проблем, способен стать рефлексивный подход к обучению.
Для нашего исследования интерес представляют работы по теории развивающего обучения психологов Л.С. Выготского, П.Я. Гальперина, И.С. Якиманской, а также педагогов Ю.К. Бабанского, И.Я. Лернера, Е.Л. Мельниковой, Л.Г. Петерсон и др.
Как отмечает Е.Л. Мельникова, современное образование медленно и трудно переходит от старой (авторитарной и репродуктивной) к новой парадигме (гуманистической и личностно ориентированной), при этом возникает необходимость пропагандировать развивающее обучение [1].
Теоретические основы развивающего обучения математике рассмотрены в исследованиях Х.Ж. Ганеева, А.Ж. Жафярова, Н.Б. Истоминой, З.И. Слепкань и др.
В работах педагогов Л.С. Бурдякова, B.А. Далингера, С.С. Кашлева, И.Г. Липатниковой, С.А. Синельникова, В.Н. Эверстовой и иных изучены роль и место рефлексии в учебно-познавательном процессе.
Вопросы развивающего обучения изучаются давно, однако тема остается актуальной до сих пор в связи с тем, что стремительно меняются условия, требования, материальные возможности в образовании. Поэтому возникает задача поиска новых современных педагогических методов и средств развивающего обучения. В качестве одного из них рассмотрим рефлексивный подход к обучению как один из определяющих факторов повышения качества образования.
Цель исследования – теоретически обосновать и экспериментально проверить педагогические условия повышения уровня обученности обучающихся 5-го класса на уроках математики посредством использования приемов рефлексии и обучения самостоятельному выбору микроцелей.
Выдвинута гипотеза, что уровень обученности обучающихся 5-го класса на уроках математики повысится, если будут созданы следующие условия:
– на уроках будут применяться различные приемы рефлексии;
– на основе выполненных приемов рефлексии обучающиеся будут самостоятельно выбирать микроцели и достигать их.
Материалы и методы исследования
Экспериментальное исследование проведено на базе МБОУ «Момская средняя общеобразовательная школа» Момского района, в 5 «б» классе, с охватом 18 обучающихся, из них 10 девочек и 8 мальчиков. Были применены теоретические (анализ психолого-педагогической литературы) и эмпирические (педагогический эксперимент, методы количественной и качественной обработки данных) методы исследования.
Результаты исследования и их обсуждение
Как утверждает И.С. Якиманская, «…раз- вивающее обучение – это обучение, ориентированное на закономерности развития личности, в котором развивающий эффект является прямым результатом. Оно рассматривает ученика как личность и создает максимум благоприятных условий для ее развития. Основные идеи развивающего обучения: развивать самостоятельное мышление ребенка, способность к его самообразованию и саморазвитию» [2, с. 144].
С.С. Кашлев определяет понятие «рефлексия» следующим образом: «Рефлексия – это процесс и результат фиксирования субъектами (участниками педагогического процесса) состояния своего развития, саморазвития и причин этого» [3, с. 105].
На смену традиционным методам обучения многими учеными предлагается рефлексивный подход, с помощью которого учебный процесс приобретает деятельностное содержание, т.е. обучающиеся, открывая новые знания, овладевают новыми методами и навыками учебной деятельности.
В научных трудах И.Г. Липатниковой рассмотрен рефлексивный подход к изучению математики в школе, «…который представляет собой системообразующий фактор и универсальный механизм управления учебным процессом на основе совместно-распределенной деятельности; исследование, осмысление и переосмысление информации учащимися, преобразования ее путем самостоятельного выбора учеником микроцелей с учетом его индивидуальных возможностей, способностей, потребностей и определение траектории развития личностных качеств» [4, с. 10].
И.Г. Липатникова подчеркивает, что для раскрытия микроцели ученик осознает: «I уровень – недостаточность имеющихся знаний и потребность в получении нового знания; II уровень – недостаточность имеющихся знаний и потребность в получении нового знания, хочет узнать причину своего индивидуального затруднения в деятельности; III уровень – недостаточность имеющихся знаний и потребность в получении нового знания, хочет и может найти новый способ действия с целью выявления причины затруднения» [5, с. 20–21].
Как отмечает Л.С. Бурдякова, задача рефлексивного подхода заключается в том, чтобы научить обучающегося контролировать свои эмоции, рационально подходить к оценке своих сильных и слабых сторон, верить в свои возможности и силы [6].
Согласимся с С.А. Синельниковым, который считает, что приобретенные «…рефлексивные умения выполняют интегративную функцию, так как являются результатом деятельности, основой формирования субъектной позиции, инструментом субъектной реализации личности; обеспечивают совершенствование и успешность любой деятельности, т.е. выполняют преобразующую функцию» [7, с. 11].
Обучаясь рефлексии, ученики параллельно учатся: самостоятельному планированию, анализу, оцениванию и коррекции собственной деятельности; постановке новых учебных микроцелей и отысканию путей их достижения. Это, в свою очередь, приводит к повышению уровня владения учебным материалом. Рефлексия может осуществляться не только в конце урока, но и на любом его этапе [8].
Для нашего исследования, в частности в структурировании урока, особый интерес вызывают предложенные Л.Г. Петерсон схемы рефлексивной самоорганизации на уроках математики [9].
Приведем пример фрагмента урока математики в 5-м классе по теме «Умножение десятичных дробей», этап – самостоятельная работа с самопроверкой по эталону.
Урок спланирован и проведен по технологии, предложенной Л.Г. Петерсон, которая считает, что «…при проведении обучающих самостоятельных работ оценивается только успех, ошибки выявляются и корректируются на основе определения их причин (т.е. правил, алгоритмов, определений, которые усвоены недостаточно). На уроках рефлексии используется самоконтроль, отметки в журнал выставляются по желанию» [9, с. 56].
Вначале обучающимся предлагается проверочная самостоятельная работа, которую они должны выполнить за 7 минут. Задание: выполните умножение десятичных дробей.
а) 8,9 ∙ 0,6; б) 4, 55 ∙ 2,2; в) 12, 344 ∙ 0,006; г) 8,14 ∙ 10; д) 46,7 ∙ 0,01.
Как отмечает в своих трудах В.А. Далингер: «Умение ставить вопросы как своим собеседникам, так и самому себе – это проявление рефлексии» [10]. Правильно поставленный вопрос, правильно сформулированная микроцель способствуют развитию умственных способностей обучающихся, помогают обосновывать выводы, самостоятельно находить ошибки и исправлять их.
Учитель должен при составлении заданий самостоятельной работы спрогнозировать ошибки, которые могут допустить обучающие при выполнении предложенной самостоятельной работы (табл. 1).
Таблица 1
Ответы и классификация возможных ошибок
|
задание |
ответ |
Классификация возможных ошибок |
|
|
а) |
8,9 ∙ 0,6 |
5,34 |
Вычислительная ошибка. Неправильно поставили запятую |
|
б) |
4,55 ∙ 2,2 |
10,01 |
Вычислительная ошибка. Неправильно поставили запятую. Оставили нуль справа после запятой |
|
в) |
12,344 ∙ 0,006 |
0,074064 |
Вычислительная ошибка. Не смогли отделить цифры запятой, если цифр в произведении не хватает |
|
г) |
8,14 ∙ 10 |
81,4 |
Умножали в столбик Неправильно поставили запятую при умножении на 10 |
|
д) |
46,7 ∙ 0,01 |
0,467 |
Умножали в столбик. Неправильно поставили запятую при умножении на 0,01 |
После выполнения самостоятельной работы проводится этап проверки по эталону, затем учитель задает следующие вопросы:
1) Кто правильно выполнил 5 (4, 3, 2, 1) заданий? Обучающиеся поднимают руки, учитель фиксирует результаты.
2) Что не получилось и почему в примере а (б, в, г, д)? Обучающиеся классифицируют ошибки (вычислительная или неправильно поставленная запятая).
3) Почему у вас возникло затруднение? Обучающиеся вспоминают соответствующее правило.
Далее с помощью учителя обучающиеся ставят микроцели по всем заданиям.
1. Микроцель ученика: научиться отделять запятой столько цифр справа, сколько их отделено запятой в обоих множителях.
2. Микроцель ученика: в конце десятичной дроби после запятой нужно вычеркнуть нуль.
3. Микроцель ученика: научиться правильно ставить запятую; если в произведении получается меньше цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей.
4. Микроцель ученика: научиться правильно ставить запятую: при умножении десятичной дроби на 10 (100, 1000…) нужно переносить запятую влево на один (два, три, …) знак(а).
5. Микроцель ученика: научиться правильно ставить запятую: при умножении десятичной дроби на 0,1 (0,01, 0,001…) нужно переносить запятую вправо на один (два, три, …) знак(а).
Следующим этапом урока является этап достижения поставленных микроцелей. На этом этапе обучающиеся выполняют упражнения из учебника, каждый раз возвращаясь к поставленным ранее микроцелям.
Обучающимся, которые не допустили ошибок, учителем предлагаются дополнительные задания повышенной сложности.
После этого была проведена аналогичная самостоятельная работа, цель которой заключается в проверке усвоения темы после проведенной работы по постановке и достижению микроцелей. Результаты этой самостоятельной работы, проверенной учителем, приведены ниже (рисунок).
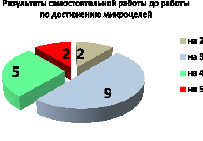
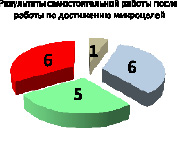
Соотнесение результатов самостоятельных работ в 5 «б» классе до и после работы над микроцелями
Как видим из диаграмм, после определения микроцелей и организованной работы по их достижению количество обучающихся, выполнивших самостоятельную работу, возросло с 88,9 % до 94,4 %, а качество выполнения – с 38,9 % до 61,1 %.
В конце урока организована рефлексия «Знаю, умею» (табл. 2): каждому ученику предлагалось заполнить карточку с таблицей, при этом выдавалась следующая инструкция: «Отметьте галочкой смайлик, который определяет, насколько данное правило вами усвоено: J – хорошо понял, K – не все понял, L – не понял. Время работы 2 минуты».
Таблица 2
Рефлексия «Знаю, умею»
|
Я знаю, что: |
Выбери смайлик |
||
|
1 – нужно отделять запятой столько цифр справа, сколько их отделено запятой в обоих множителях |
J |
K |
L |
|
2 – в конце десятичной дроби после запятой необходимо вычеркнуть нуль |
J |
K |
L |
|
3 – если в произведении не хватает цифр, то надо сначала приписать впереди столько нулей, сколько не хватает цифр, а потом в целой части поставить нуль |
J |
K |
L |
|
Я умею: |
Выбери смайлик |
||
|
4 – умножать десятичную дробь на 0,1(0,01; 0,001…), при этом переношу запятую влево на один (два, три, …) знак(а) |
J |
K |
L |
|
5 – умножать десятичную дробь на 10 (100, 1000…), при этом переношу запятую вправо на один (два, три, …) знак(а) |
J |
K |
L |
Анализ рефлексии «Знаю, умею» по теме «Умножение десятичных дробей» (табл. 3) показал, что обучающиеся 5-го класса еще не все могут корректно оценивать свои знания и умения, тем не менее проводить данную работу необходимо с целью обучения правильной самооценке.
Таблица 3
Результаты самооценки обучающимися 5 класса по методике «Знаю, умею»
|
J |
K |
L |
|
|
1 |
15 |
3 |
0 |
|
2 |
14 |
3 |
1 |
|
3 |
14 |
3 |
1 |
|
4 |
13 |
5 |
0 |
|
5 |
13 |
5 |
0 |
Результаты рефлексии показывают, что 13 респондентов считают, что очень хорошо поняли решение всех пяти заданий, в то время как по итогам самостоятельной работы (диаграмма 1) на «5» написали только 6 человек, а на «4» – 5. Знак затруднения отметили два разных ученика (один на втором примере, другой – на третьем), значит, они считают, что правильно решают четыре примера из пяти, однако с самостоятельной работой не справился 1 ученик, и 6 респондентов получили «3». Таким образом, установлено, что для обучающихся 5-го класса при недостаточной сформированности самооценки необходимо постоянно создавать условия для оценивания ими результатов собственной учебной деятельности через рефлексию, что будет способствовать гармоничному развитию личностных качеств младших школьников.
Проведенная после изучения темы «Умножение и деление десятичных дробей» контрольная работа также показала, что использование рефлексии положительно повлияло на качество обученности: на «5» написали 5 обучающихся, на «4» – 7, на «3» – 5 и на «2» – 1.
Заключение
Таким образом, подтвердилась выдвинутая гипотеза, что уровень обученности обучающихся 5-го класса на уроках математики повысится, если будут созданы следующие условия:
– на уроках будут применяться различные приемы рефлексии;
– на основе выполненных приемов рефлексии обучающиеся будут самостоятельно выбирать микроцели и достигать их.



