В настоящее время анализ точности вероятностных моделей получил широкое распространение в областях, связанных с проблемами Big Data: теории алгоритмов [1], проектировании машинного обучения [2, 3], исследовании социальных сетей [4], вычислительной механике [5], энергетике [6] и т.д. Авторы настоящей статьи показали, что представления о точности вероятностных моделей являются важным компонентом формирующегося у студентов вероятностного подхода к научному познанию [7]. Также авторы доказательно утверждают, что наиболее естественным было формирование вероятностного подхода в ходе освоения студентами вероятностных и статистических курсов в рамках их математической подготовки [8]. В то же время в российской университетской среде до сих пор бытует отношение к вероятностному подходу как к чему-то второстепенному, вспомогательному. Причины такого отношения, с одной стороны, известны, с другой – нуждаются в дальнейшем анализе, что и будет сделано в настоящей статье. Также в научно-методической литературе практически отсутствуют рекомендации по формированию представлений о точности вероятностных моделей, которые невозможно дать без вычислительных экспериментов, часть из которых будет представлена в результатах исследования.
Основной целью настоящего исследования является развитие методики формирования представлений студентов о точности вероятностных и статистических моделей.
Материалы и методы исследования
Задачи исследования:
Во-первых, авторы продолжают исследования по формированию вероятностного подхода студентов к научному познанию [9], одной из составляющих которого является представление учащихся о точности вероятностных моделей. В целом проблема остается дискуссионной. Необходим поиск новых аргументов в ее поддержку, поскольку именно сильная или слабая опора преподавателя на вероятностный подход определяет методику преподавания теории вероятностей и математической статистики в вузе.
Во-вторых, авторы ставят задачу усовершенствовать методику формирования компетенций студентов в сфере точности вероятностных моделей, которая востребована в научной и проектной практике. В работе [7] авторы исследовали следующие частные случаи сопоставления точных и приближенных моделей.
1. Проведено исследование изменения формы полигона биномиального распределения при увеличении числа опытов. Графическими средствами показано, что уже при 20 опытах полигон распределения несимметричного биномиального распределения близок к дискретизации соответствующего нормального распределения. Результаты были продемонстрированы студентам в весеннем семестре 2020/2021 учебного года, планируются к использованию в дальнейшем в курсе теории вероятности. Этот этап исследования можно считать завершенным.
2. Проведено сравнение вычисленных на интервалах значений вероятностей по точной формуле Бернулли и по приближенной интегральной теореме Лапласа. Построен график изменения относительной ошибки с ростом числа опытов, демонстрирующих ее убывание по обратной корневой зависимости. В то же время само значение ошибки нельзя признать удовлетворительным. Результаты были продемонстрированы студентам в весеннем семестре 2020/2021 учебного года, планируется дальнейшее исследование вопроса.
3. Проведено сравнение вычисленных вероятностей редких событий по точной формуле Бернулли и приближенной формуле Пуассона. Визуальное сравнение полигонов не дает возможности заметить расхождение уже при 20 опытах. Таким образом, графики не являются наглядными для демонстрации в студенческой аудитории, что порождает необходимость в дополнительном исследовании, результаты которого представлены в настоящей статье.
4. Проведено сравнение вычисленных интервальных вероятностей редких событий по точной формуле Бернулли, по приближенной формуле Пуассона и по приближенной интегральной теореме Лапласа. При числе опытов, равном 100 и 1000, названные значения практически совпадают. С одной стороны, это дает студентам уверенность в возможности применения приближенных формул вместо точных при возникновении необходимости в подобных расчетах в профессиональной деятельности. С другой стороны, полученные результаты не дают представления о динамике ошибки в приближенных расчетах. Это обстоятельство и послужило одним из побудительных мотивов к настоящему исследованию.
Результаты исследования и их обсуждение
Прежде всего рассмотрим дискурс вероятностного подхода в российской науке и практике высшей школы. Существующее неоднозначное отношение к вероятностному подходу объясняется как объективными, внешними, так и субъективными, внутривузовскими причинами. Во-первых, в отечественной науке в 1930–1950-е гг. сложилось противопоставление детерминистского, одобряемого и вероятностного, «сомнительного» подхода к научному познанию [10]. Для преодоления этой антитезы, синтеза подходов в рамках единого системного потребовались годы, но устойчивые представления отчасти сохраняются («вероятностный детерминизм» [11]). Проявляется это противопоставление в вузовских курсах с учетом признанной инерционности образовательной системы. Во-вторых, в ряде отраслей, связанных с обороной и безопасностью, к вероятностным моделям относятся настороженно, поскольку цена даже одной человеческой жизни велика [12]. В то же время к вероятностным моделям в экономике и бизнесе, где риски угрожают преимущественно финансовым активам, отношение всегда было более лояльным [13]. В-третьих, значительная часть вузовских преподавателей математики не уделяют должного внимания формированию вероятностного подхода у студентов, поскольку «не одобряют» эвристических оснований теории вероятностей и математической статистики по сравнению со строгими основаниями математического анализа и линейной алгебры. Люди, проникшиеся с детства красотой и гармонией логических построений, стараются «не замечать» хаотичности окружающего мира. Вероятность явно противоречит архетипическому представлению о математике как о точной науке. Такие преподаватели предпочитают «задерживаться» на изложении абстрактной теории вероятностей (комбинаторики и геометрических вероятностей), «не успевая» добраться до статистики, в том числе такого важнейшего стохастического инструмента, как регрессионный анализ. Разумеется, таких взглядов придерживаются далеко не все математики. В качестве наиболее ярких примеров, созвучных авторскому подходу к теории вероятности, можно назвать работы Н.П. Пучкова [14] и Г.Д. Гефана [15]. Ссылки на исследования других сторонников приближения вероятностных курсов к практико-ориентированным задачам можно найти в цитированных выше работах авторов.
Таким образом, формирование вероятностного подхода к научному познанию студентов не является авторской инновацией и находится в поле определенной полемики со сторонниками осовремененного и завуалированного детерминистского подхода. Не отвергая важности детерминистского подхода, авторы настаивают на его равноправии с вероятностным в рамках единого системного подхода к научному познанию.
Для поиска эффективных методических средств формирования у студентов представлений о точности вероятностных моделей был проведен ряд вычислительных экспериментов, для выполнения и анализа результатов которых в качестве соавторов были привлечены предмагистранты, закончившие бакалавриат в зарубежных университетах. Целью экспериментов был анализ точности приближенной формулы Пуассона для оценки вероятности наступления редких событий в зависимости от числа опытов.
Задача 1. Событие А может наступить в одном опыте с вероятностью р = 0,005. Сравнить вероятности непоявления события А: Р (Х = 0), появления одного Р (Х = 1), двух Р (Х = 2), трех Р (Х = 3) или четырех Р (Х = 4) событий А в серии из n опытов, вычисленные по точной формуле Бернулли РВ = 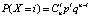 и приближенной формуле Пуассона РР = =
и приближенной формуле Пуассона РР = = 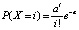 , где q = 1 – p = 0,995, для n от 625 до 10000 с соответствующим изменением a = np от 0,125 до 2,00.
, где q = 1 – p = 0,995, для n от 625 до 10000 с соответствующим изменением a = np от 0,125 до 2,00.
Для оценки точности приближения Пуассона были вычислены абсолютная ошибка Δ = PB – PР и относительная ошибка ε = Δ / PB , графики изменения которых с ростом числа опытов приведены на рис. 1 и 2.
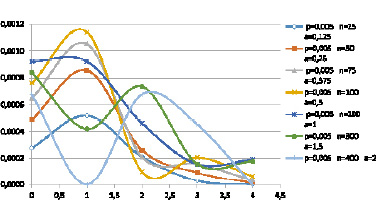
Рис. 1. Зависимость абсолютной ошибки Δ от числа опытов n в задаче 1
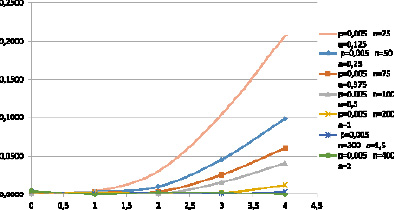
Рис. 2. Зависимость относительной ошибки ε от числа опытов n в задаче 1
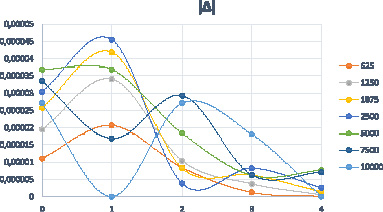
Рис. 3. Зависимость абсолютной ошибки Δ от числа опытов n в задаче 2
Задача 2. В условиях задачи 1 событие А может наступить в одном опыте с вероятностью р = 0,0002. Сравнить вероятности непоявления события А: Р (Х = 0), появления одного Р (Х = 1), двух Р (Х = 2), трех Р (Х = 3) или четырех Р (Х = 4) событий А в серии из n опытов, вычисленных по точной формуле Бернулли и приближенной формуле Пуассона, с q = 1 – p = 0,9998, для n от 625 до 10000 с соответствующим изменением a = np от 0,125 до 2,00. Таким образом, интенсивности потока события, связанные со значениями параметра a, одинаковы для обеих задач.
Как и для задачи 1, для оценки точности приближения Пуассона были вычислены абсолютная ошибка Δ = PB – PР и относительная ошибка ε = Δ / PB , графики изменения которых с ростом числа опытов приведены на рис. 3 и 4.
Для обеих задач очевидно, что с ростом числа опытов величина относительной ошибки ε снижается (рис. 2, 4). Тем не менее, сопоставляя результаты вычисления относительной ошибки для n от 25 до 400 (рис. 2) со случаем изменения n от 625 до 10 000 (рис. 4), можно отметить неудовлетворительную точность вычислений в первом случае (ошибка доходит до 20 %). Разумеется, этот факт объясняется влиянием ошибок округления, которые при сравнении малых величин становятся сопоставимыми с ошибками приближения по формуле Пуассона. При вычислении же абсолютной ошибки Δ не требуется выполнять деление малых величин. Именно поэтому значения абсолютной ошибки в обоих случаях свидетельствуют о достаточно высокой точности вычисления – погрешность составляет не более 1 % (рис. 1, 3). Однако осциллирующий характер абсолютной ошибки Δ (рис. 1, 3) не позволяет сделать вывод о ее монотонном снижении с увеличением числа опытов, как в случае относительной ошибки ε (рис. 2, 4). В любом случае студентам следует учитывать возможное влияние ошибок округления при вычислении вероятностей, связанных с редкими событиями.
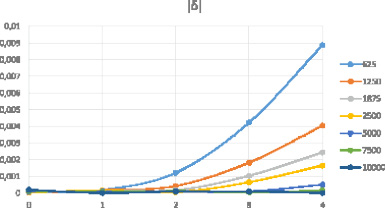
Рис. 4. Зависимость относительной ошибки ε от числа опытов n в задаче 2
Следует отметить, что ведущим фактором точности вычислений является даже не общее число опытов, а величина вероятности появления редкого события. Результаты при р = 0,0002 (задача 2) получаются значительно более точными, чем при р = 0,005 (задача 1). Этот вывод подтверждается данными таблицы, представленными для случая Р (Х = 0) (таблица).
Относительная ошибка вычисления вероятности непоявления редкого события в серии из n опытов для разных значений его вероятности р
|
р = 0,005 |
n |
25 |
50 |
75 |
100 |
200 |
300 |
400 |
|
| ε | |
0,0003 |
0,0006 |
0,0009 |
0,0013 |
0,0025 |
0,0038 |
0,0050 |
|
|
р = 0,0002 |
n |
625 |
1250 |
1875 |
2500 |
5000 |
7500 |
10000 |
|
| ε | |
0,00001 |
0,00002 |
0,00004 |
0,00005 |
0,0001 |
0,0002 |
0,0002 |
Вероятность непоявления редкого события Р (Х = 0) и связанная с ней вероятность появления хотя бы одного редкого события P(X ≥ 1) = 1 – P(X = 0) являются важнейшими параметрами в теории надежности сложных систем, а также при моделировании защиты от катастроф, эпидемий и других опасных и причиняющих вред явлений. Именно поэтому на значение точности вычисления вероятности непоявления разрушительных по последствиям событий следует обращать внимание студентов.
Заключение
Проведенное исследование позволило найти новые аргументы для обоснования важности формирования вероятностных компонентов научного мировоззрения студентов. Анализируя мнения явных и скрытых оппонентов вероятностного подхода, авторы пришли к выводу, что основу их позиции составляют представления об опасности «неточных» вероятностных методов при моделировании вредоносных явлений. Поэтому авторы обратили особое внимание на совершенствование механизмов формирования у студентов компетенций в области точности вероятностных и статистических моделей, границ применимости некоторых из них. Результаты вычислительных экспериментов показали достоинства и ограниченность использования приближенной формулы Пуассона вместо точной формулы Бернулли при вычислении вероятностей редких событий, к разряду которых как раз и относятся природные и техногенные катастрофы. Полученные рекомендации полезны тем студентам, чья профессиональная деятельность будет связана с построением математических моделей в технико-экономической сфере.



