Анализ данных и машинное обучение – это предметная область, которая с каждым годом все больше внедряется во все сферы человеческой деятельности. В связи с этим увеличивается спрос на данных специалистов, и вузы активно внедряют данную область в процесс обучения студентов математических и информационных специальностей, а также в подготовку будущих учителей математики и информатики [1]. Однако, несмотря на большое количество исследований и публикаций в области применения машинного обучения в различных сферах, работ, посвященных методике обучения анализу данных и машинному обучению, в отечественной и зарубежной литературе достаточно мало. Методические особенности обучения студентов в области анализа данных и машинного обучения недостаточно изучены.
Предметная область анализа данных и машинного обучения находится на стыке трех фундаментальных областей: математика, информатика и область исследования (физика, сельское хозяйство, экономика и т.п.). Следовательно, при подготовке специалистов в данной области необходимо обучать и показывать важность каждой из представленных областей, то есть придерживаться принципа междисциплинарной интеграции [2]. Одним из наиболее эффективных средств применения междисциплинарной интеграции является метод проектов [3]. Рассмотрим пример использования метода проектов как инструмент междисциплинарной интеграции в обучении студентов анализу данных и машинному обучению.
Цель исследования: описать методику обучения студентов анализу данных и машинному обучению на основе междисциплинарной интеграции и метода проектов и проверить ее эффективность.
Материалы и методы исследования
При применении данного подхода лучше всего работать с реальными данными и решить актуальную для конкретного региона задачу [4]. В частности, представленная работа посвящена прогнозированию спроса на велосипеды на уровне станции и пустых доков в системе совместного использования велосипедов на базе станции, сочетая стохастическое моделирование и подход на основе анализа данных. Одним из вызовов этой проблемы, который будет рассмотрен, является оценка спроса при ограничениях цензуры, т.е. когда спрос удовлетворяется только в том случае, если на станции нет избыточного спроса. Стохастическое моделирование будет использовано для имитации станции и оценки скорости прибытия и убытия велосипедов в системе как независимых процессов Пуассона в неоднородной по времени модели очередей [5].
На данном этапе обучаемые должны четко обозначить проблему, основываясь на данных. Также необходимо определить актуальность решаемой задачи, как она может помочь в будущей профессиональной деятельности. В частности, в нашем проекте совместно со студентами мы должны прийти к выводу, что перебалансировка велосипедов крайне важна для операторов, чтобы удержать постоянных клиентов. Если на станции наблюдается избыточный спрос, вероятность ситуации, когда клиент не найдет велосипед или свободный док на соседней станции, возрастает, поэтому система в конечном итоге может стать слишком ненадежной, что вынудит клиента купить собственный велосипед или перейти на менее экологичный вид транспорта. В результате они вынуждены осуществлять разбалансировку, даже если на нее приходится большая часть эксплуатационных расходов.
Таким образом, на первом этапе определяется решаемая задача (классификация, регрессия или кластеризация), целевая функция и признаки, которые на нее влияют.
Следующий этап связан с предобработкой данных, их визуализацией и подготовкой датасета к применению методов машинного обучения. Студенты должны решить проблемы с пропусками, с выбросами, с мультиколлинеарностью признаков, посмотреть разбалансировку данных, уникальные значения, распределения данных, нормализации или стандартизации и т.д. Таким образом, применяя методы математической статистики, привести датасет к наиболее оптимальному виду для последующего применения методов машинного обучения [6].
Особо важным этапом является этап определения математического аппарата. Именно здесь вводятся математические понятия и связи между ними, которые в дальнейшем будут реализованы в программном коде. Из опыта проведения занятий отметим, что необходимо привлекать студентов к дискуссии, обсуждать с ними все понятия и обозначения, спрашивать о том, где они раньше встречались с данными понятиями, на каких дисциплинах и т.п. В частности, в данном проекте мы обсуждаем стохастическую модель системы совместного использования велосипедов на одной станции, которая может быть использована для получения оценок скорости отправления и прибытия в заданное время. Необходимо совместно ввести следующие основные обозначения и определения.
1. Процесс обновления – это стохастический процесс, описываемый как:
, 
,
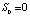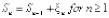где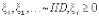 
.
2. Однородный процесс Пуассона – это процесс возобновления, такой, что время между событиями распределено экспоненциально, т.е. для некоторого действительного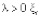 
имеет экспоненциальное распределение, т.е. распределение с плотностью 
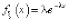при x ≥ 0. Параметр λ называется скоростью однородного пуассоновского процесса. Однородный по времени процесс имеет функцию интенсивности λ(t).
3. Процедура подсчета Nt = argmaxk{sk ≤ t} подсчитывает количество случаев, когда событие произошло к моменту времени t и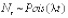 
, т.е.
,
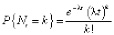E(Nt) = λt.
для любого временного интервала размером t.
Необходимо, чтобы студенты рассматривали статьи ученых по данной тематике, о том, какие еще задачи можно решать, используя данный математический аппарат.
Также совместно со студентами вводятся определенные допущения, ограничения использования данного метода, вводятся оценка коэффициентов прибытия и убытия, оценка коэффициентов прибытия и отправления в периоды повышенного спроса. В частности, при оценке коэффициентов прибытия и убытия приходим к следующим выводам: для процесса числа событий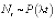 
, если Nt событий наблюдаются в интервале [t1, t2], то оценка интенсивности на станции j по максимуму правдоподобия имеет вид:
.
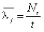Используя наблюдения за доступностью станции в течение дня, мы можем разделить временной интервал дня на интервалы с однородными пуассоновскими процессами прибытия и убытия на каждом из них и оценить интенсивность для каждого временного интервала для каждого дня, а затем взять их среднее значение. Эта оценка является несмещенной:
.
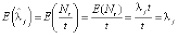Дисперсия равна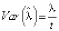 
. Тогда, усредняя оценки для многих реализаций, мы получим более точные результаты.
Чтобы оценить коэффициенты прибытия и отправления в часы пик для конкретной станции, мы должны помнить, что в часы пик один из коэффициентов является ненаблюдаемым, поэтому мы должны скорректировать нашу формулу, чтобы включить только часть временного интервала, когда станция не была полностью заполнена или пуста в течение каждого дня.
,
,
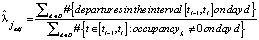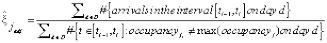где D – набор дней, используемых для оценки, а в знаменателе – количество наблюдений в данном интервале, для которых заполненность не равна максимальной заполненности или 0 для скорости отправления и скорости прибытия, соответственно.
К сожалению, в большинстве случаев данный этап в обучении студентов пропускают и переходят сразу к построению моделей. Авторы считают, что данный этап является очень важным и именно здесь закладываются компетенции, которые помогут студентам проходить собеседования в ИТ-компаниях и убеждать работодателей в глубоком понимании в области анализа данных и машинного обучения.
На этапе математического моделирования необходимо провести имитацию изолированной станции и проверить эффективность модели на интервалах ненаблюдаемого спроса, выбрать временные горизонты, определиться с метриками. Совместно со студентами еще раз проговариваются следующие допущения:
– Интенсивности прибытия и отправления станции являются пуассоновскими процессами.
– Все наблюдения проводятся при одинаковых погодных условиях и по дням недели. Это означает, что для полного моделирования реальной станции нам потребуется оценить ставки в нескольких сценариях и чередовать расчетные ставки для прогнозов в разную погоду.
– Если станция пользуется избыточным спросом, клиенты не ждут на станции. Пользователи имеют доступ к опубликованной в приложении и на сайте информации в реальном времени о количестве велосипедов на каждой станции.
Время между прибытиями в процессе Пуассона распределено экспоненциально, а экспоненциальное распределение обладает свойством отсутствия памяти. Благодаря этому мы можем моделировать время прибытия как равномерно распределенное в пределах каждого шага с фиксированной скоростью.
На следующем этапе, при построении моделей машинного обучения, необходимо определиться с метриками качества обучения, а также предложить студентам сравнить работу 3-5 различных моделей для задачи регрессии. Кроме этого, студенты должны оптимизировать данные модели, находить наиболее оптимальные гиперпараметры и уметь объяснять это с точки зрения математики. То есть на данном этапе математическая подготовка студентов также присутствует.
Что касается нашей задачи, для сравнения мы выбрали линейные регрессии Ridge, Lasso и алгоритм случайного леса. Параметр Alpha для регрессий Ridge и Lasso был настроен на выбор из нескольких значений. Для получения стабильных результатов мы применили кросс-валидацию. Ожидается, что случайный лес даст наилучшие результаты, так как это сильный ансамблевый алгоритм, устойчивый к переборке и включению бесполезных переменных. Один набор целевых значений был установлен равным заполненности станции через один час с момента прогнозирования, другой набор целевых значений отражал заполненность станции через два часа. Для этих моделей были выбраны следующие признаки: велосипедов в момент прогнозирования; велосипедов 1 час назад; велосипедов вчера; минута и час в момент прогнозирования. Такой набор переменных делает их сравнимыми с нашей моделью, так как она обучена в предположении, что погодные условия одинаковы в течение всего периода прогнозирования. Это позволяет нам сравнить предсказательную силу этих моделей с предложенной моделью. Предложенная модель превзошла Random Forest на временном горизонте 30 минут, но Random Forest показал лучшие результаты при прогнозировании на горизонтах 1 и 2 часа (рисунок).
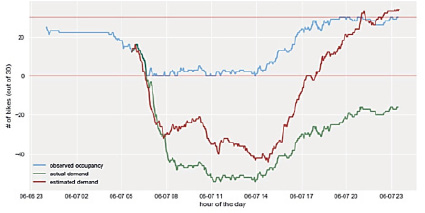
Результаты работы модели
Далее необходима дискуссия. Совместно со студентами приходим к выводу, что эти результаты относятся к случаю одинаковых погодных условий, тогда как в реальности заполняемость зависит от погодных условий. Тем не менее мы считаем, что использование погодных характеристик может улучшить нашу модель: имея обширный набор данных и информацию о погоде, можно вручную разделить данные на части с похожими погодными условиями, чтобы оценить различные показатели интенсивности по нескольким сценариям, а затем изменить соотношение между оцененными функциями интенсивности при прогнозировании заполняемости в зависимости от прогноза погоды. Однако использованная нами модель не может быть заменена Random Forest для всех целей, поскольку наша модель делает возможным прогнозирование ненаблюдаемого спроса, что не может быть достигнуто при обучении модели, использующей только наблюдаемые данные в качестве целевых переменных.
На заключительном этапе обязательно необходимо сделать выводы и обсудить перспективы дальнейшего исследования.
В нашем проекте мы совместно приходим к следующим выводам. Результаты, полученные в данном исследовании, показывают, как моделирование занятости станции как комбинации независимых пуассоновских процессов прибытия и отправления может быть использовано для прогнозирования фактического спроса на велосипеды, несмотря на то что он не может наблюдаться в состояниях избыточного спроса. Мы показываем, что оценка показателей интенсивности на исторических данных как кусочно-постоянной функции, использующей только те моменты времени, когда наблюдаются оба показателя, помогает избежать недооценки величины этих показателей.
Направление дальнейших исследований может заключаться в построении приближенной к реальным условиям модели, учитывающей погодные условия. Этого можно достичь путем ручного разделения данных на части с похожими погодными условиями, с осадками или без них, чтобы оценить различные показатели интенсивности по нескольким сценариям, а затем изменять оценочные функции интенсивности при прогнозировании заполняемости в зависимости от прогноза погоды.
Таким образом, в результате реализации междисциплинарного подхода в обучении студентов анализу данных и машинному обучению на основе метода проекта студенты, решая актуальную задачу, знакомятся со всеми этапами, видят «подводные камни» на каждом из этапов, применяют теоретические знания в области математики на реальном примере.
Выводы
Описанная выше методика обучения студентов в области анализа данных и машинного обучения была реализована в Финансовом университете при Правительстве РФ и показала высокую степень эффективности. Эффективность доказана следующими факторами:
Педагогический эксперимент. В качестве промежуточного контроля обучаемым контрольной и экспериментальной групп было предложено творческое домашнее задание, максимально приближенное к реальной профессиональной задаче. Студентам необходимо самостоятельно собрать большой набор данных (более 50 000 объектов по 15-20 признакам) и решить задачу обучения с учителем и без учителя, обосновав весь математический аппарат. После чего разработать рекомендательную систему по предсказанию целевой функции. Результаты выполнения задания экспериментальной группы значительно превзошли результаты контрольной группы (тема отдельного исследования).
Студенты без особых проблем проходят собеседование и поступают на работу в качестве специалистов в области анализа данных, машинного обучения в крупные банки (Сбербанк, «Тинькофф», «Открытие», «Райффайзенбанк», «Газпром банк» и т.д.) и крупные компании и группы.
Большинство выпускных квалификационных работ студентов связаны с анализом данных и машинным обучением. Данные работы, как правило, отмечаются государственной экзаменационной комиссий и получают оценку «отлично».
В настоящее время методика междисциплинарного подхода в обучении студентов анализу данных и машинному обучению на основе метода проекта внедрена в обучение студентов по направлению «Прикладная информатика» в ФГБОУ ВО «Российский государственный аграрный университет – МСХА имени К.А. Тимирязева» и подготовку будущих учителей математики и информатики в Марийский государственный университет.