Математическое моделирование движения автотраспортных средств в настоящее время имеет огромную область применения. Согласно требованиям Министерства транспорта РФ, математическое моделирование применяется при принятии управленческих решений на стратегическом, тактическом и опративном уровнях организации дорожного движения, так как это наиболее точный и удобный инструмент, позволяющий усовершенствовать существующую транспортную систему.
Сами математические модели транспортных потоков в настоящее время разделяют на макроскопические, мезоскопические и микроскопические. Макроскопическое моделирование устанавливает функциональные зависимости между отдельными показателями потока, например скоростью, плотностью и иинтенсивностью движения. При микроскопическом моделировании детально имитируется движение транспортных средств с целью установления показателей эффективности функционирования локального участка сети. Обычно имитационная модель базируется на статистическом распределении интервалов между транспортными средствами. Мезоскопическое моделирование служит «мостом» между микро- и макромоделями. Мезоскопические модели рассматривают единичные транспортные средства, но описывают их движение и взаимодействие на основании статистических зависимостей.
При решении отдельных задач может отдаваться предпочтение тому или иному методу моделирования, либо можно использовать комбинацию методов.
Одной из проблем, влияющих на удобство передвижения по улично-дорожной сети, являются дорожно-транспортные происшествия (ДТП). Как правило, при ДТП перекрывается одна из полос для движения, образуется «узкое место», которое становится причиной заторов. Аналогичная ситуация может возникнуть при проведении дорожных работ.
Ввиду этого актуальной становится проблема моделирования движения автомобилей при объезде места дорожно-транспортного происшествия или дорожно-ремонтных работ.
Целью исследования является повышение качества организации движения транспортных потоков в случае дорожно-транспортного происшествия.
Задача исследования – разработка математической модели и определение характеристик движения потока автомобилей при объезде мест дорожно-транспортных происшествий или дорожно-ремонтных работ.
Материалы и методы исследования
При моделировании движения автомобилей в местах ДТП возможно применять различные типы моделирования.
Так, например, в работе [1] для моделирования ДТП использовались макроскопические переменные, такие как средняя плотность и средняя скорость. Данный подход достаточно упрощен, но позволяет прогнозировать влияние дорожно-транспортных происшествий на средние характеристики потоков. В работе [2] объединено стохастическое моделирование аварий с моделью Лайтхилла – Уизема – Ричардса (LWR). L. Jin и S. Amin в своей работе [3] представили модель динамики движения на автостраде при дорожно-транспортных происшествиях со стохастическим снижением пропускной способности. В их модели с помощью цепей Маркова моделируется сокращение пропускной способности дороги, определяются характеристики очереди, вызванной инцидентом на дороге. Использовать результаты работы [3] можно для анализа влияния стохастических колебаний пропускной способности на пропускную способность участка автострады.
Для описания модели движения автомобилей в местах ДТП можно также использовать подход авторов, описывающих транспортные потоки при пересечении блок-постов [4] или при движении через «бутылочное горло» [5].
В данной работе для моделирования движения автотранспортных средств вблизи места дорожно-транспортного происшествия будем использовать метод, относящийся к мезоскопическому моделированию. Базовые гипотезы и положения, характеризующие транспортные потоки, были описаны, например, в статье автора [6]. Транспортная сеть представляется в виде ориентированного графа. Необходимые сведения об организации движения, параметрах транспортных потоков содержатся в матрицах ASTREETS и BINTERSECTION. Информация о числе транспортных средств, проходящих от «источника» к «стоку» в течение времени t, содержится в OD-матрице (матрице корреспонденций) [7].
Распределение интервалов по времени в каждом из транспортных потоков по каждой из полос движения принято подчиненным распределению Эрланга. Данное распределение позволяет аппроксимировать с нужной степенью точности при правильном подборе параметров любое статистическое распределение [8]. Кроме того, такая гипотеза о распределении интервалов в случайном потоке позволяет с помощью метода псевдосостояний использовать цепи Маркова и определять характеристики функционирования системы массового обслуживания [8, 9].
Результаты исследования и их обсуждение
Рассмотрим движение автотранспортных средств в плотном транспортном потоке в случае, когда в результате дорожно-транспортного происшествия или ремонтных работ перекрывается движение по одной из полос.
1. Представление места ДТП как системы массового обслуживания
Будем рассматривать отрезок улично-дорожной сети между двумя соседними перекрестками, на котором произошло ДТП или ведутся ремонтные работы, как открытую систему массового обслуживания. Движение транспортных средств в плотном потоке, прибывающих по двум полосам к точке А (рис. 1), в данном случае замедляется. Согласно натурным наблюдениям, образуется общая очередь перед точкой А, несмотря на то, что автомобили располагаются на двух полосах. Дисциплина очереди – обслуживание в порядке прибытия транспортных средств (в порядке поступления заявок) FIFO. Количество мест в очереди ограничено количеством автомобилей, которые могут заполнить обе полосы от точки А до предшествующео узла сети (перекрестка) – точки С. Под временем обслуживания T0 будем понимать среднее время (в секундах) объезда первым в очереди автомобилем препятствия AB. Интенсивность обслуживания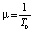 
.
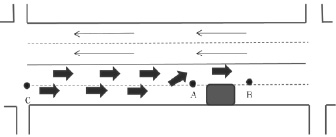
Рис. 1. Схема движения в месте ДТП
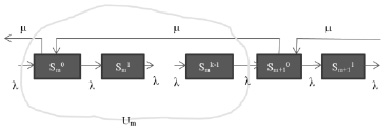
Рис. 2. Псевдосостояния модели системы массового обслуживания
2. Разработка математической модели движения автотранспортных средств в плотном потоке при ДТП
Согласно модели TIMeR_Mod интервалы по времени между транспортными средствами по каждой из полос распределены по закону Эрланга. Проведенные натурные обследования показали, что для плотного потока можно считать, что это специальный закон Эрланга порядка k ≥ 4. Для расчетов параметров распределения Эрланга можно использовать результаты работы [10].
Пусть потоки П1 и П2 распределены по специальному закону Эрланга с параметрами λ1 и λ2 соответственно и с одинаковым значением параметра k ≥ 4. Тогда «на обслуживание» прибывает поток П1+2 Пальма, распределение интервалов по времени между событиями в котором – это специальное распределение Эрланга такого же порядка k с параметром λ = λ1 + λ2. Время обслуживания будем считать распределенным по показательному закону с параметром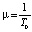 
. В очереди могут находиться одновременно не более N автомобилей, а в системе в целом – (N + 1) автомобиль: N в очереди и один на обслуживании.
Для составления математической модели данной СМО воспользуемся методом псевдосостояний.
Опираясь на граф состояний (рис. 2), составим систему дифференциальных уравнений Колмогорова, описывающих пребывание СМО в псевдосостояниях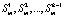 
состояния 
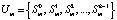, где 
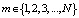. Вероятность нахождения СМО в кждом из псевдосостояний зависит в общем случае от времени t. Будем обозначать как 
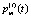вероятность пребывания системы в состоянии 
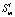, где 
.
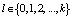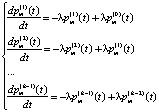(1)
Обыкновенное дифференциальное уравнение для пребывания СМО в псевдосостояни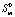и 
при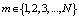 
имеет вид
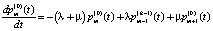. (2)
Подмножество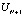 
состоит из одного псевдосостояния 
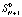, поэтому соответствующее дифференциальное уравнение имеет вид
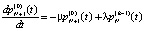. (3)
Таким образом, система дифференциальных уравнений Колмогорова для составляемой модели массового обслуживания имеет следующий вид:
, 
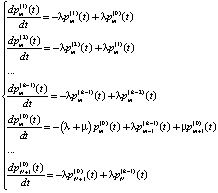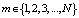. (4)
Кроме того справедливо равенство
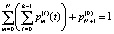. (5)
Начальные условия следующие:
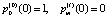для 
, 
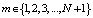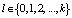. (6)
Вероятность того, что в момент времени t на участке улично-дорожной сети BC находится m автомобилей – это вероятность того, что система массового обслуживания пребывает в состоянии Um. Эта вероятность Pm вычисляется следующим образом:
, 
: 
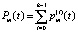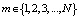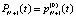. (7)
Ситуация, сложившаяся на участке улично-дорожной сети, описывается следующими характеристиками СМО:
1) вероятность того, что в момент времени t данный участок загружен полностью, равна
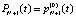; (8)
2) среднее количество автомобилей на данном участке дороги в момент времени t равно математическому ожиданию числа автомобилей в очереди в данный момент:
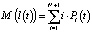; (9)
здесь l(t) – случайная величина, число автомобилей в очереди в момент времени t;
3) среднее время проезда (в секундах) по участку AC улично-дорожной сети равно
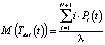, (10)
здесь Tdel(t) – случайная величина, время проезда по участку AC улично-дорожной сети автомобиля, находящегося в i-й позиции в очереди в момент времени t.
3. Характеристики движения автотранспортных средств в плотном потоке при дорожно-транспортном происшествии
Время функционирования системы массового обслуживания может быть разделено на два временных участка:
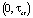– вероятности пребывания заявки в конкретном состоянии зависят от времени;
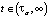– вероятности пребывания заявки в конкретном состоянии не зависят от времени (стационарное состояние).
Если дорожно-транспортное происшествие только что произошло, то следует рассматривать функционирование системы на промежутке (0, τst). В данном случае основная трудность состоит в решении системы дифференциальных уравнений (4). Найти точное аналитическое решение возможно лишь при отдельных конкретных значениях параметров λ и μ. Поэтому при решении поставленной практической задачи гораздо удобнее найти численное решение системы для заданного момента t1. Например, это можно сделать методом Рунге – Кутты. После определения численных значений вероятностей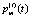 
в момент t1 можно вычислить необходимые показатели функционирования системы по формулам (8)–(10).
Однако, как показывают практические исследования, через достаточно короткое время τst после дорожно-транспортного происшествия, система переходит в стационарное состояние. Поэтому на промежутке (0, τst) можно считать вероятности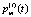 
постоянными величинами, не зависящими от времени t. Следовательно, их производные по времени равны нулю.
Тогда система (1) принимает вид
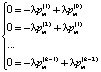(11)
Отсюда следует, что
,
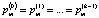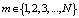. (12)
Учитывая результат (12) и дифференциальные уравнения (2) и (3), получим систему алгебраических уравнений
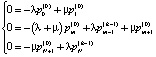
для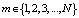 
. (13)
Обозначим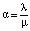 
. Решение системы:
, 
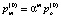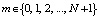. (14)
Значение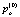 
выразим из условия (5):
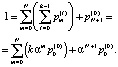
Таким образом:
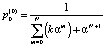. (15)
Теперь выразим необходимые характе- ристики:
1) вероятность того, что данный участок загружен полностью, равна
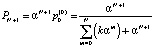; (16)
2) среднее количество автомобилей на данном участке дороги AC:
.
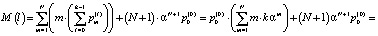
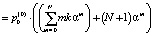Итак,
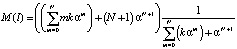; (17)
3) среднее время проезда по участку AC улично-дорожной сети равно
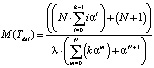. (18)
В модели TIMeR_Mod, разработанной ранее Н.А. Наумовой, информация о распределении потоков по сети содержится в матрицах ASTREETS и BINTERSECTION [6]. Характеристики (16)–(18) позволяют разработать алгоритм корректировки данных о транспортных потоках при ДТП:
а) ес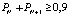ли 
или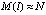 
, то «исключаем» движение по рассматриваемому участку улично-дорожной сети в матрицах ASTREETS и BINTERSECTION (вводим запрет на движение соответствующим образом, изложенным в работе [6]);
б) есл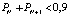и 
и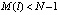 
, то уменьшаем количество полос движения в месте инцидента в матрицах ASTREETS, BINTERSECTION и корректируем параметры Эрланга на полосах движения;
в) обновляем OD-матрицу согласно изменениям, внесенным ASTREETS и BINTERSECTION [7].
Разработанная модель движения автомобилей в случае сужения проезжей части по причине ДТП или дорожно-ремонтных работ позволяет оперативно корректировать организацию движения.
Заключение
Моделирование движения транспортных потоков вблизи мест дорожно-транспортных происшествий или ремонтных работ позволяет прогнозировать вызванные этим задержки транспортных средств и корректировать оптимальные схемы организации движения в этих ситуациях. В данной работе применялись методы мезоскопического моделирования, отличительной особенностью которых является оперативность выполнения расчетов при соблюдении необходимой точности. Результаты данной работы дополняют модель движения транспортных потоков TIMeR_Mod, разработанную ранее автором настоящей статьи.