В последнее столетие наблюдается постепенный рост среднегодовых температур воздуха во всем мире, регулярно фиксируются температурные рекорды и климатические аномалии [1]. Глобальное потепление набрало особенно высокую скорость в последние десятилетия и в силу этого способно вызвать множество последствий, которые коренным образом могут поменять мир, в котором мы привыкли жить. Это и затопление прибрежных территорий Мировым океаном вследствие таяния ледников, и наступление пустынь в аридной зоне, и изменения в биосфере планеты, и многое другое. Одним из подобных последствий может оказаться масштабная деградация многолетней мерзлоты в северных широтах, которая усугубляется тем фактом, что в Арктике потепление климата выражено еще сильнее. Сложно оценить экологические, экономические и социальные риски, связанные с резким разрушением криолитозоны. Некоторыми из имеющих место процессов для детального изучения этих рисков могут служить возможная потеря устойчивости грунтов под инженерными сооружениями или эрозия почв на берегах водоемов [2].
Многолетнемерзлые породы (ММП) распространены в арктической и субарктической климатических зонах, а также в горных районах. Их толщина может достигать 500 м и более. В настоящее время температура мерзлых пород находится в пределах нескольких градусов ниже нуля, поэтому их оттаивание может начаться в скором времени.
В Центральной Якутии в настоящее время имеет место слабый отклик глубины сезонно-талого слоя и в целом теплового состояния ММП на наблюдаемое повышение температуры воздуха [3]. В основном это объясняется синхронным уменьшением высоты снежного покрова и, следовательно, уменьшением его теплоизолирующей способности. Однако на окраинах криолитозоны в других регионах происходит деградация ММП [4]. Например, на северо-востоке европейской части России и на севере Западной Сибири. В Печоро-Уральском регионе по результатам мониторинга отмечаются рост температуры мерзлых пород, рост глубины таликов и осадка грунтов [5]. На территории Уренгойского месторождения в Западной Сибири идет устойчивое повышение температуры верхних горизонтов пород, а в некоторых местах произошел отрыв кровли ММП и ее продвижение вниз идет со скоростью примерно 30 м/100 лет [6]. В приведенных работах указывается, что, за исключением Центральной Якутии, измеренное повышение температуры ММП отстает от повышения температуры воздуха в 2–7 раз.
В работе [7] проведено моделирование температурного режима грунтов за последние 3,5 млн лет на территории Уренгойского месторождения. В разработанной очень подробной модели учтены зависимости коэффициента теплопроводности породы от фазового состава порового флюида, его зависимость от температуры, зависимость температуры таяния льда от давления и солености, а также возможное наличие незамерзшей воды в мерзлых грунтах. Моделирование показало, что за рассмотренный период произошло как минимум 10 циклов похолодания, которые сопровождались появлением слоя ММП и зоны стабильности газовых гидратов. Выявлено, что температурное поле находится в сильной зависимости от физико-химических свойств грунтов, в особенности от коэффициента теплопроводности. В работе [8] построен прогноз изменений температуры грунтов в Центральной Якутии при двух сценариях потепления – умеренный со скоростью 0,04 °C/год и агрессивный со скоростью 0,08 °C/год. Согласно использованной модели даже при агрессивном сценарии температура приповерхностного грунта поднимется выше 0 °C только через 40 лет. При этом глубина сезонного оттаивания при тренде 0,04 °C/год практически не меняется, а при тренде 0,08 °C/год – увеличивается с 2,0 до 2,2 м. Также следует отметить, что в этой модели потепление климата на 1 °C вызывало повышение температуры грунтов на 0,33 °C.
В настоящей работе ставится цель провести анализ темпов деградации слоя ММП при возможном повышении атмосферной температуры с помощью математической модели, предложенной в работе [7].
Материалы и методы исследования
Согласно модели из [7], для массива горных пород решается одномерная задача Стефана по глубине
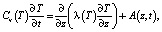 (1)
(1)
где Cv(T) – объемная теплоемкость пористой среды, зависящая от её состава, температуры и глубины залегания и в которую включена теплота фазового перехода «лед – вода»; T – температура горных пород; t – переменная времени; z – глубина; λ(T) – коэффициент теплопроводности пористой среды, зависящий от ее состава, температуры и глубины залегания; A – внутреннее тепловыделение горных пород, вызванное естественной радиоактивностью.
Объемная теплоемкость пористой среды вычисляется как взвешенная средняя арифметическая по ее составу:
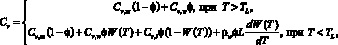 (2)
(2)
где TL – температура плавления льда; Cv,m – объемная теплоемкость скелета пористой среды, которая находится из исследований керна; ϕ – пористость среды, которая зависит от глубины и также определяется из исследований керна; Cv,w – объемная теплоемкость воды, равная 4,187 МДж/(м3· °С); W(T) – доля незамерзшей поровой воды, которая зависит от температуры и типа горных пород; Cv,i – объемная теплоемкость льда, равная 1,926 МДж/(м3· °С); ρw – плотность воды, равная 1000 кг/м3; L – удельная теплота плавления льда, равная 334 кДж/кг.
Температура плавления льда зависит от гидростатического давления, содержания солей в поровой воде натрий- и калийхлоридного типа
TL = 0 °C – 0,073P – 0,064Cs, (3)
где TL – температура замерзания воды в °С, P – давление в МПа, Cs – концентрация солей в г/л.
Коэффициент теплопроводности пористой среды вычисляется как средняя геометрическая по ее составу:
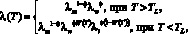 (4)
(4)
где λm – коэффициент теплопроводности скелета пористой среды, который зависит от температуры; λw – коэффициент теплопроводности воды, тоже зависящий от температуры; λi –коэффициент теплопроводности льда, который принят равным 2,26 Вт/(м∙ °С).
Коэффициент теплопроводности скелета пористой среды находится по следующей зависимости от температуры:
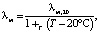 (5)
(5)
где λm,20 – коэффициент теплопроводности скелета при 20 °С, который определяется из исследований керна; αT – температурный коэффициент.
Коэффициент теплопроводности воды также зависит от температуры:
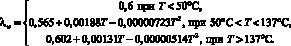 (6)
(6)
На верхней границе задается условие 3-го рода, учитывающее конвективный и радиационный теплообмен
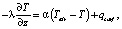 (7)
(7)
гд α – суммарный коэффициент теплообмена между атмосферным воздухом и грунтом, Tair – температура воздуха, qsurf – радиационный баланс земной поверхности.
На нижней границе массива горных пород задается условие 2-го рода с геотермическим потоком тепла
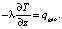 (8)
(8)
Для единственности решения системы уравнений (1)–(8) математическую модель необходимо дополнить начальным условием
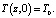 (9)
(9)
Поставленная задача решается методом конечных элементов с использованием пакета прикладных программ для технических вычислений.
Объектом исследования является неоднородный массив горных пород глубиной 3000 м, из которых в условиях Центральной Якутии примерно на 500 верхних метрах расположены ММП, а на оставшуюся часть приходятся талые горные породы. Для сокращения краевых эффектов используется неравномерная сетка разбиения, шаг которой постепенно уменьшается при приближении к верхней границе. Начальное распределение температуры массива горных пород по данным термометрии представлено на рис. 1. Видно, что температурное распределение в большей части мерзлой зоны практически равномерное с близкими к нулю отрицательными температурами. Это может свидетельствовать о том, что в настоящий момент ММП находятся на пороге начала оттаивания.
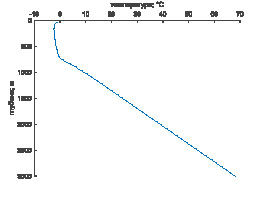
Рис. 1. Начальное распределение температуры горных пород по глубине
В расчетах содержание незамерзшей воды в мерзлых песчаных породах, а также содержание солей в поровой воде принимаются равными нулю. Также для условий Центральной Якутии приняты усредненные значения A = 1,5·10–6 Вт/м3, αT = 0,002 °С–1, qgeo = 0,057 Вт/м2. Физические параметры многослойного массива горных пород представлены в табл. 1. Данные по среднемесячной температуре воздуха и по радиационному балансу земной поверхности, приведенные в табл. 2, взяты из работы [9]. Значения суммарного коэффициента теплообмена (табл. 2) рассчитаны с учетом снежного покрова, который препятствует поступлению холода и, соответственно, понижению температуры верхних горизонтов ММП в зимний период.
Таблица 1
Характеристики слоев массива горных пород
|
Интервал, м |
Плотность скелета пористой среды, кг/м3 |
Объемная теплоемкость скелета пористой среды, МДж/( °С∙м3) |
Коэффициент теплопроводности скелета пористой среды, Вт/(м∙ °С) |
Пористость, д.е. |
|
0–86 |
2000 |
2,13 |
2,24 |
0,21 |
|
86–488 |
2000 |
2,27 |
2,12 |
0,21 |
|
488–539 |
2120 |
2,37 |
1,77 |
0,19 |
|
539–980 |
2300 |
2,18 |
2,39 |
0,13 |
|
980–1831 |
2350 |
2,19 |
2,72 |
0,12 |
|
1831–2561 |
2380 |
2,19 |
2,86 |
0,12 |
|
2561–3000 |
2330 |
2,19 |
2,51 |
0,12 |
Для проверки адекватности численной модели проведено сравнение среднемесячных температур грунта на глубине 3,2 м с наблюдениями на площадке с естественным покровом на стационаре «Туймаада» ИМЗ СО РАН [10] (рис. 2). В этом расчете для верхнего граничного условия (7) использованы архивные данные по погоде с сайта rp5.ru, а также данные по радиационному балансу луговой площадки из табл. 2.
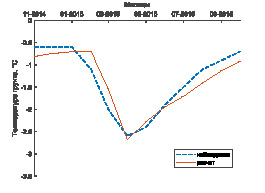
Рис. 2. Начальное распределение температуры горных пород по глубине
Расчетные и наблюдаемые на стационаре кривые совпадают в достаточной мере.
Таблица 2
Среднемесячные значения данных атмосферы на начальный момент расчета
|
Месяц |
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
XI |
XII |
|
Средняя месячная температура воздуха, °С |
–37,5 |
–32,7 |
–21,4 |
–5 |
7,3 |
16,6 |
19,8 |
15,4 |
5,8 |
–7,4 |
–27,6 |
–38 |
|
Радиационный баланс, Вт/м2 |
–9,65 |
–4,63 |
–5,02 |
45,14 |
113,04 |
126,16 |
119,6 |
79,48 |
35,49 |
0 |
–14,27 |
–9,65 |
|
Коэффициент теплообмена между атмосферным воздухом и грунтом, Вт/(м2· °С) |
0,39 |
0,40 |
0,43 |
9,28 |
27,87 |
27,46 |
26,19 |
25,30 |
24,38 |
8,89 |
0,54 |
0,42 |
Рассматриваются две скорости будущего потепления климата: 1) рост температуры воздуха с темпом 4 °С/100 лет; 2) рост с темпом 2 °С/100 лет. Первая скорость соответствует повышению температуры поверхности Земли при отсутствии дополнительной деятельности по уменьшению выбросов CO2, согласно докладу МГЭИК [1]. Вторая скорость соответствует целевому уровню увеличения средней температуры планеты, согласованному на конференции по климату в Париже в 2015 г. [11]. В течение каждого года температура воздуха задается циклически изменяющейся функцией, аппроксимирующей его среднемесячные значения. Так как моделирование проводится на срок, составляющий 300 лет, то повышение температуры воздуха в ХХI в. линейно экстраполируется на два последующих столетия.
Расчеты выполнены в коммерческом пакете прикладных программ для решения задач технических вычислений.
Результаты исследования и их обсуждение
На рис. 3 представлены распределения температуры по глубине в верхней толще мерзлых пород для двух рассмотренных сценариев потепления климата. После 100-го года при тренде увеличения температуры воздуха 2 °С/100 лет (рис. 3, a) и после 50-го года при тренде 4 °С/100 лет (рис. 3, b) заметны повышения температур пород, находящихся ниже сезонно-талого слоя глубиной до 3 м. Потепление климата провоцирует деградацию многолетней мерзлоты и увеличение глубины сезонного оттаивания, что может приводить к развитию термокарста при наличии сильнольдистых ММП, термоэрозии и термоденудации. Видно, что профили температуры в талой области имеют практически линейный характер. Следовательно, при потеплении климата тепловая энергия, подводимая на земную поверхность, в основном расходуется на плавление порового льда в верхних горизон- тах ММП.
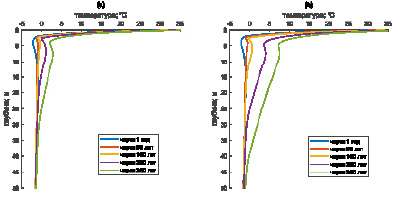
Рис. 3. Динамика распределения температуры по глубине в осенний период при темпе роста температуры воздуха: (a) 2 °С/100 лет (b) 4 °С/100 лет
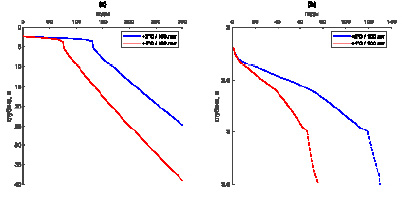
Рис. 4. (a) Прогнозная динамика изменения глубины кровли ММП в зависимости от сценария потепления климата. (b) Прогнозная динамика изменения глубины сезонного оттаивания ММП в зависимости от сценария потепления климата. Пунктирные линии – глубина кровли ММП после отрыва от поверхности
На рис. 4, a, представлены прогнозные глубины кровли ММП на период до 300 лет при действии темпов потепления климата на 2 °С/100 лет и 4 °С/100 лет. При этом в течение первых 60 и 120 лет, соответственно темпам потепления, растепление грунтов находится в пределах сезонно-талого слоя глубиной 3 м (рис. 4, b). Через 50 лет глубина сезонно-талого слоя увеличится на 30 см (13 %) при темпе потепления климата 2 °С/100 лет и на 50 см (23 %) при темпе потепления 4 °С/100 лет. Этот результат близок к значениям Росгидромета [12], согласно которому в районе г. Мирный к середине XXI в. ожидается увеличение глубины сезонного оттаивания на 20 % – с 1,95 м (2000–2010 гг.) до 2,34 м (2040–2050 гг.).
В дальнейшем происходит отрыв кровли ММП и ниже сезонно-талого слоя начинает формироваться таликовая зона, которая со временем увеличивается по линейному закону (рис. 4, a). Эта зона растет со скоростью примерно 12 м/100 лет при темпе потепления климата 2 °С/100 лет и примерно 15 м/100 лет при темпе потепления климата 4 °С/100 лет.
Погрешности результатов данного моделирования в наибольшей степени зависят от упрощающих допущений модели и качества исходных данных. Во-первых, сильное влияние на термическое состояние ММП оказывает растительность (возможно уменьшение мощности сезонно-талого слоя до 50 %) [13], вариации которой в данной работе не учитываются. Во-вторых, выходные данные МОЦ несут в себе определенную неточность, которая может быть довольно существенной для территории Якутии [14]. И в-третьих, теплофизические свойства грунтов могут значительно меняться в зависимости от местности.
Заключение
Проведен вычислительный эксперимент по определению масштабов оттаивания многолетней мерзлоты при двух сценариях потепления климата для условий Центральной Якутии. Использована численная модель, разработанная для палеореконструкции теплового режима горных пород. При темпе роста температуры воздуха 4 °С/100 лет, что соответствует сценарию с отсутствием дополнительной деятельности по уменьшению выбросов CO2, через 60 лет начинается деградация многолетней мерзлоты со скоростью примерно 15 м/100 лет. В случае если темп потепления климата удержится на отметке 2 °С/100 лет, то деградация многолетней мерзлоты начнется через 120 лет, а ее скорость составит примерно 12 м/100 лет. Эти прогнозные оценки получены при изменениях температуры в верхних горизонтах ММП, обусловленных только повышением температуры воздуха. Дополнительные исследования необходимы для оценки влияния многолетней динамики снежного покрова, солнечной радиации, альбедо земной поверхности, скорости ветра и других региональных характеристик климата на термическое состояние криолитозоны.



