Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

При рассмотрении аспектов деятельности логистических систем внимание уделяется факторам неопределенности, влияющим на нее [1]. Торгов-посредническая сеть как подсистема логистики является сложной, включает в себя множество торгово-посреднических организаций [2], осуществляющих широкую гамму операций [3]. Наличие большого числа связей в такой системе характеризует ее разветвленную структуру, что осложняет задачи управления процессами распределения, доставки и хранения грузов различного назначения. При этом обработке подлежит огромное количество данных, требующих структуризации и последующего формирования информации о состоянии и функционировании системы. Выделим факторы, обусловливающие наличие неопределенности при управлении логистической системой, в обобщенном виде.

1. В процессе анализа функционирования торгово-посреднической сети рассматриваются элементы, которые характеризуются как качественными, так и количественными показателями. Преобладание качественных показателей не означает получение точных оценок, поскольку их формализация строится на нечетких данных.

2. Недостаток знаний, снятие которого обусловлено эффективным применением интеллектуальных, информационных и иных ресурсов. Пополнение знаний дает информацию о поведении логистической системы, что позволяет в последующем принимать решения об эффективном управлении по отношению к другим участникам рынка.

3. Наличие огромного количества данных, полученных в результате мониторинга логистической системы. Такого рода проблема относится к Big Data, и ее разрешение требует научных изысканий, связанных с разработкой и применением инструментальных средств системного анализа и обработкой имеющихся данных.

4. Отсутствие обмена данными между конкурирующими фирмами, например о состоянии спроса и предложения на реализуемый товар, затрудняющее возможность прогнозирования рыночного спроса.

5. Поиск целенаправленных решений по управлению товарными потоками, в процессе которых требуется формальная постановка цели, целиком зависящая от наличия опыта и знаний менеджеров.

6. Использование детерминированных данных и методов для решения функций логистики, тогда как без должного внимания и применения остаются данные стохастического характера, что свидетельствует о получении неэффективных и не вполне обоснованных решений.

7. Особое место в логистической системе занимают вопросы цены на микрорынках торгово-посреднической сети, сохранения баланса между спросом и предложением. Неопределенность в этом случае вызвана несогласованностью законов функционирования рыночных отношений с результатами, требующими строгого выявления циклически повторяющихся взаимосвязанных процессов, отражающих протекание взаимосвязанных событий.

Неопределенность следует относить к существенному фактору, накладывающему свой отпечаток на вопросы, касающиеся выполнения системного анализа и поиска эффективных решений для получения конечного результата, что свидетельствует о необходимости снятия неопределенности в решении задач логистики.

Материалы и методы исследования

Рассматривая понятие неопределенности применительно к логистической системе, заметим следующее: неопределенность – недостаток достоверной информации о протекающих событиях или процессах и различных состояниях как внутренней, так и внешней среды. Предлагаемые к рассмотрению факторы накладывают свой отпечаток на реализацию задач логистики. Затруднительно получить данные, проанализировать и структурировать их с целью получения информации, которая могла бы быть достаточной для получения дополнительных знаний с целью снятия неопределенности. Отсутствие достаточных реализаций в данном направлении способствует лишь возрастанию неопределенности.

При рассмотрении логистической системы среди источников возникновения неопределенности выделяют три взаимосвязанных фактора ее порождения [4].

1. Сложность системы, обусловленная наличием большого числа связей – как структурных, так и функциональных, присутствующих между агентами торгово-посреднической сети. Тем самым ее формальное описание весьма затруднительно по причине изменчивости структуры, функций выполнения заданий, иерархии управления и др.

2. Человеческий интеллект предполагает наличие достаточных способностей к познанию, пониманию и решению проблем, связанных с необходимостью выполнения контроля, осуществления эффективного управления логистическими процессами.

3. Внешняя среда является нейтральной, дружественной и антагонистичной по отношению к логистической системе. Ее игнорирование ограничивает возможности в получении достоверной информации и последующей выработке и принятии решений. Рассмотрение объектов логистики в виде замкнутой системы существенно увеличивает неопределенность, тем самым утрачивается возможность объективного анализа.

Вышеуказанные факторы следует отнести к причинам, вызывающим неопределен- ность [5].

1. Недостаток сведений, обусловленный несовершенством развития инфраструктуры информационной системы поддержки бизнес-процессов; отсутствием или недостатком статистических данных; возможными ошибками в проектировании и моделировании; несовершенством применения инструментов анализа логистических процессов.

2. Случайные или преднамеренные противодействия со стороны поставщиков (вызванные неопределенностью спроса на продукцию и трудностями ее сбыта) и конкурентов (не стремящихся делиться своей информацией, старающихся вникнуть в коммерческие тайны и воздействовать на внутренние дела фирмы).

3. Действие внешних факторов, имеющих случайную, неожиданную и, следовательно, труднопредсказуемую природу возникновения.

Упомянутые факторы относятся к объективной реальности недостаточно точного и однозначного познания окружающей среды, поскольку степень освоения и применяемые методы анализа логистических процессов требуют дополнительных ресурсов.

По существу, неопределенность порождает необходимость в решении задач по двум направлениям: 1) выполнение мониторинга, сбор и обработка данных, определение степени неопределенности информации; 2) анализ неопределенности, оценка состояния системы, прогнозирование и выработка сценариев развития и управления процессами.

При рассмотрении неопределенности как фактора участия в устойчивом функционировании торгово-посреднической сети степень неопределенности определяет своевременность, качество и количество информации.

Продвижение товара в торгово-посреднической сети, несмотря на выполнение договорных отношений, включающих в себя детерминированные значения данных, не исключает наличия событий случайного характера. С учетом накопления данных о доставке, хранении и продаже товаров, выполнения их ретроспективного анализа рассматриваемые события (исходы) являются вероятными. Здесь находит свое отражение вероятностная мера. С позиции математики она является функцией вещественной, определенной на множестве событий в вероятностном пространстве, удовлетворяющей таким положительным свойствам, как счетная аддитивность [6].

Состояние элементов и всей торгово-посреднической сети меняется. Зная возможные исходы конкретной ситуации, следует ответить на вопрос, насколько она вероятна. Ответ может быть получен на основе применения инструментов обработки статистических данных, когда первое, что приходит в голову, – определить такие показатели, как дисперсия, математическое ожидание, среднеквадратическое отклонение, размах и др. Следует отметить, что имеющие место и широко применимые инструменты для этих целей дают неточные оценки при работе с Big Data. Тем не менее, вероятностная мера как статистический параметр является отправной точкой для последующего измерения неопределенности.

Наличие неопределенности обусловливает сложность системного анализа логистических процессов и требует применения теории вероятности. В таких случаях приходится рассматривать исходы ситуаций, когда неопределенность связана с незнанием всего набора причинно-следственных связей или когда причина влияния на исход явно видна, но имеющиеся в нашем распоряжении теории затруднительно использовать на практике [7]. Если отказаться от пути применения весьма затратного механизма предсказания конкретных исходов, то следует перейти к предсказаниям того, что, вероятно, случится, зная заранее возможные исходы.

Рассмотрим пример. На микрорынках торгово-посреднической сети покупки осуществляются как регулярно, так и несистематически. На формирование набора товара с фиксированным количеством и ценой влияют различные факторы. Определенные виды товара приобретают стабильно в постоянных объемах, другие – случайным образом. При этом качество и цена товара могут меняться. Фактически дело обстоит так: существует столько причин для событий обмена, сколько и самих событий.

Несмотря на то что технологическая конкуренция на рынке товаров и услуг является двигателем прогресса, она остается мощным фактором генерирования вопросов, требующих изучения и разрешения, что исключает попытки выполнения точного моделирования рыночного обмена по причине непостоянства спроса. Следовательно, торгово-посредническая сеть как элемент логистики – идеальный кандидат для вероятностного моделирования.

Сведения, полученные в результате мониторинга, являются объектом хранения, передачи, преобразования и рассматриваются как информация. Измерение количества информации есть мера, основанная на понятии энтропии. Ее применение связано с рассмотрением состояний, в которых находится торгово-посредническая сеть. Большинство из этих состояний имеют стохастическую природу возникновения, должны быть конечными и наделены счетным числом исходов. Например, при рассмотрении цены X на микрорынке она описывается множеством величин х1, x2, ..., xn. Это же можно сказать и об объемах продаж. Этим состояниям соответствуют вероятности p1, p2, ..., pn появления величин х1, x2, ..., xn. Значения величин и полученные в результате расчета вероятности образуют статистический ансамбль данных, необходимых для вычисления энтропии.

В процессе анализа состояния сети полученные значения вероятностей требуют подтверждения гипотезы о распределении случайной величины. Если гипотеза подтверждена наличием статистического распределения вероятностей рk, то информационная энтропия определяется по выражению:

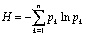(1)

при условии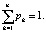

В случае, когда гипотеза не получила подтверждения, формула (1) теряет свой смысл. Фактически H – средняя величина энтропии в расчете на одно состояние или исход. Рассматривая (1), следует выделить свойства: 1) величина Н = 0 возможна, когда какое-либо из pk равно 1, а остальные – нулю. Свойство свидетельствует об отсутствии неопределенности информации; 2) величина Н будет максимальной (неопределенность в информации максимальна), когда все вероятности равны между собой. Тогда невозможно отдать предпочтение какому-либо из рассматриваемых состояний. Если неопределенность в системе будет стремиться к минимуму (к меньшей величине энтропии), следовательно, она способна реализовать меньше состояний [8]. Среди положительных качеств энтропии выделяют свойство аддитивности: энтропия всех рассматриваемых исходов равна сумме энтропий отдельных исходов. Выражению (1) присуще еще одно качество: порядок (расстановка) слагаемых не влияет на величину Н, т.е. можно поменять местами любое число слагаемых, но значение Н при этом не изменится. Однако данное качество нельзя отнести к положительным, поскольку (1) не отражает наличия суперпозиции.

При анализе состояния торгово-посреднической сети с использованием при этом измерения неопределенности информации по (1) появляется возможность выбора из многообразия альтернатив для последующего принятия решений. Также можно определить меру разнообразия или индекса разнообразия, который применяется для определения степени равномерности или однородности распределения значений выборки, где pk соответствует числу исходов в выборке и рассчитывается по выражению: 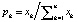. Если для всех N исходов или всей выборки распределение непрерывной случайной величины является равномерным, то согласно (1) получим максимальное значение энтропии через log2N, что соответствует о наибольшей степени разнообразия состояний. При отсутствии разнообразия значение энтропии будет равно нулю. Если абстрагироваться от присущей энтропии единицы измерения «бит», допустимо нормирование индекса: H/Hmax.

Торгово-посредническая сеть, обладающая большим числом структурных и функциональных связей, находится в неравновесном, но стационарном состоянии. Переход системы к равновесному состоянию будет означать рост энтропии, стремление к максимальному значению. Однако такое состояние свидетельствует об утрате возможностей развития системы, которое может быть только за счет снятия неопределенности информации. В этом процессе учет лишь смены состояний и определение величины энтропии не дают полной картины его протекания. Тем самым использование понятия энтропии не позволяет в целом охарактеризовать структурное содержание системы и функционирование ее элементов.

Одной из задач, касающихся измерения неопределенности информации, служит процедура выборки из данных, полученных в результате наблюдения за состоянием сети. Здесь важным вопросом является следующий: какие параметры следует отнести к наиболее существенными, характеризующим изучаемый процесс. Большинство данных содержится во временных рядах, а выбор необходимого набора параметров относится к процедуре параметризации. Она служит для получения новой информации о состояниях сети. При рассмотрении временных рядов и их анализе полагают, что они являются непрерывными, стационарными и линейными. Существующую в них случайную компоненту относят к разряду несущественных и в процессе анализа часто относят к ошибке измерений. Однако большинство временных рядов параметров, например движение материального потока по сети, порождены случайными динамическими процессами. Такие временные ряды нестационарны, стохастичны и нелинейны, что накладывает серьезные ограничения на применение многих традиционных методов анализа. Это обусловливает востребованность более эффективных подходов к анализу нестационарных рядов, среди которых выделяют построение гистограммных временных рядов. С ними можно ознакомиться в работах [9, 10], а также применительно к задачам логистики [11].

При рассмотрении сети ее состояние описывают набором параметров, характер и число которых существенно зависят от постановки задачи анализа. Как было отмечено ранее, можно воспользоваться энтропийной параметризацией, т.е. расчетом энтропии. Существует ряд методов, включающих в себя понятие элементарной энтропии выборки или выборочной энтропии. Выборка – это конечная совокупность значений временного ряда {xk}, выбранных по принятому правилу. Согласно задаче анализа, выбирается некоторое число значений и составляется последовательность, т.е. выборка. Значения выборки xk служат для вычисления вероятности pi(x) попадания рассматриваемого значения x в выделенный подинтервал i, что в конечном итоге позволяет вычислить первую выборочную энтропию Шеннона:

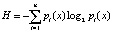. (2)

Рассмотрим подробнее применение (2) для статистического ряда, в котором значений N выборки велико. Вычисляют максимальное хmax и минимальное xmin значение в исследуемом ряде. Разделяют его на n подинтервалов (уровней) (хmax – xmin) таким образом, чтобы величина интервала Δx была не меньше доверительного интервала данных наблюдений. Далее в каждом из подинтервалов находят число попавших значений выборки {xk} и определяют относительную частоту встречаемости, т.е. вероятность pi попадания в i подинтервал значения из выборки:

pi = Ni/N

при условии 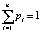, а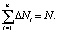

Результаты исследования и их обсуждение

Имеются временные ряды (табл. 1) продажи товаров в течение года [12]. Рассматривая ряды, отметим, что при расчете энтропии не требуется выполнения процедуры разбиения ряда на подинтервалы, поскольку он разбит на временные интервалы.

Анализируя полученные значения энтропии, отметим, что энтропия Шеннона – особенная характеристика, которая представляет собой количественную оценку отклонения данного распределения стоимости (ее амплитуды) по месяцам от однородного, когда все уровни равномерно заполнены, а вероятности всех 12 событий равны между собой. Таким образом, значения Hi характеризуют степень вариабельности процесса продаж. При нулевой вариабельности амплитуда Hi не меняется со временем. Например, стоимость реализации свитеров в январе, апреле и ноябре составляла примерно 1200 тыс. руб., что подтверждено амплитудой Hi = 0,087 (однако для данных месяцев по количеству и цене продаж нулевая вариабельность амплитуды будет отсутствовать). При максимальной вариабельности процесса продаж (когда ежемесячные значения равны между собой) средневзвешенное значение энтропии, полученное по (2), достигает своего максимального значения, равного log2n, где n – число месяцев (временных интервалов). В рассматриваемом примере максимальное значение энтропии стоимости H = 3,585. Средние значения энтропии (табл. 2) каждого товара очень близки между собой, что свидетельствует о сходстве вариабельности и относительно умеренных доходах от продажи в течение года. Следовательно, присутствуют известные закономерности распределения дохода (как случайной величины) во времени.

Интервальные Hi и средневзвешенные H значения энтропии по каждому из показателей продаж могут сопоставляться между собой для выявления амплитудных характеристик продаж. Кроме этого, значения энтропии отражают интенсивность и направления эволюции экономических процессов генерации цен, объемов продаж и стоимости. Анализируя вариабельность временных рядов, отметим следующее.

1. Большая вариабельность связана с ситуацией, когда Hi (или 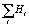, что характеризуется как аддитивность) принимает значения, близкие к максимальным, свидетельствующие о чрезвычайной интенсивности и нестабильности процессов генерации.

2. Небольшая вариабельность соответствует наличию относительно спокойной фазы.

Заключение

Рассматривая неопределенность как фактор недостатка информации о поведении системы логистики, можно заметить, что ее объективная реальность обусловлена:

– достатком необходимой информации;

– отсутствием должных невозможностей в получении данных и достоверных информаций;

– недостатком уровня знаний;

– отсутствием острой потребности в инструментах системного анализа логистических процессов.

Измерение неопределенности информации через величину энтропии предоставляет возможность аналитику оценивать состояние логистической системы и осуществлять выбор из многообразия альтернатив для последующего принятия решений.

Структура торгово-посреднической сети описывается набором параметров состояния, характер и число которых существенно зависят от постановки задачи анализа. При использовании параметризации энтропии, т.е. выборочной энтропии Шеннона, она в задаче анализа будет количественно характеризовать произвольное распределение таких параметров, как цена, стоимость, объем продаж и др. Таким образом, энтропия, являясь функцией состояния анализируемой сети, количественно характеризует меру неопределенности и отражает изменение параметров.

Исследование выполнено при финансовой поддержке РФФИ и Республики Хакассия в рамках научного проекта № 19-47-190001.