Системный подход к обеспечению качества продукции военного назначения на послепродажных стадиях жизненного цикла, т.е. при ее эксплуатации и применении, представленный в ряде работ [1–3], основан на объединении общей целью поставщиков, потребителей (эксплуатантов) продукции и сервисных центров. Стабильное качество эксплуатируемой продукции – результат стабильного функционирования системы сохранения качества (ССК), ее устойчивости. Обеспечение и поддержание стабильности ССК требуют соответствующих инструментов прогнозирования, оценки и анализа ее устойчивости. На основании результатов анализа и оценки должны приниматься обоснованные решения, разрабатываться и выполняться соответствующие действия по поддержанию устойчивости ССК.
Выбор метода моделирования для описания деятельности ССК определяется двумя условиями: особенностями системы и требованиями к степени неопределенности модели. Для разработки математической модели функционирования ССК, позволяющей прогнозировать ее возможные состояния и переходы между ними, оценивать и анализировать ее устойчивость, необходимо отметить основную особенность ССК продукции военного назначения у эксплуатанта. Объекты деятельности ССК – различная продукция военного назначения, условия и результаты ее эксплуатации – носят случайный характер, что и определяет деятельность ССК как стохастический процесс. Поэтому прогнозирование результатов деятельности ССК невозможно методами экстраполяции, использования апостериорной информации, опыта предшествующей или смежной деятельности. Деятельность такой системы не может быть представлена дальнейшим «прочерчиванием траектории из прошлого». Будущее состояние системы определяется только ее состоянием на данный момент времени и может прогнозироваться только по ее исходному состоянию, без опоры на какой-либо предшествующий опыт [4–6].
Степень неопределенности модели зависит от достоверности допущений, предположений и упрощений в описании поведения системы, изменчивости параметров, на которых должно основываться решение, обусловлена изменениями обстоятельств, появление или характер которых являются неопределенными [7–9]. С учетом этих требований и ограничений в составе возможных для моделирования ССК методов оказываются байесовский анализ и байесовские сети, Анализ дерева событий (ЕТА), Анализ дерева отказов (FTA), Анализ причинно-следственных связей (ССА), марковский анализ, методы нечеткой логики ((fuzzy logic) [10–12].
Возможность применения марковского анализа к моделированию любой системы, описание ее деятельности множеством дискретных состояний и переходов между ними, прогнозирование ее состояний независимо от ее состояния в прошлом в наибольшей степени соответствуют требованиям к моделированию деятельности ССК. С учетом этого для моделирования ССК выбраны как наиболее адекватные марковский анализ и цепь Маркова, визуализирующая возможные состояния системы и переходы между ними с оценкой их вероятности [13–15].
Цель проведенного исследования, результаты которого представлены в настоящей статье, – разработка марковской модели системы сохранения качества продукции военного назначения при ее эксплуатации и применении для определения вероятности изменения ее устойчивости и переходов в другие ее возможные состояния при ее функционировании.
Марковский процесс – модель системы сохранения качества продукции при эксплуатации
Деятельность системы сохранения качества (ССК) продукции военного назначения (ПВН) у эксплуатанта на территории инозаказчика представляет собой последовательность случайных событий с различными результатами, вероятность получения которых может быть спрогнозирована по известному их состоянию на данный момент времени. Состояния, которые принимает ССК при выполнении своих функций, и переходы между ними могут быть смоделированы марковским процессом [10–12] – цепью Маркова с матрицей перехода.
Разработка модели ССК методом марковского анализа включает описание состояний системы, которые она может принимать (с установлением вида и степени влияния на выполняемые функции), и описание переходов из одного состояния в другое.
Цепь Маркова в виде ориентированного графа (орграфа) визуализирует связи и переходы между возможными состояниями системы. Состояния системы описываются с оцениванием вероятности нахождения системы в них.
Модель ССК в виде цепи Маркова представляет собой совокупность Сn состояний и переходов из состояния i в состояние j с вероятностью Pij (где i, j = 1, 2, 3…n).
Состояния, которые с различной вероятностью может принимать система сохранения качества ПВН, определяются ролью, степенью управляемости и эффективностью деятельности каждого из ее элементов. Элементы системы – это ее участники: организация – изготовитель (поставщик) ПВН, эксплуатант и сервисный центр (СЦ) [1–3]. Их степень управляемости и уверенности в получении запланированного результата различна и оценивается вероятностью осуществления ими своих функций в системе. Различные по своей природе риски, сопровождающие деятельность каждого из участников системы, и неравные их возможности для анализа и обработки рисков наиболее адекватно могут быть смоделированы в виде шести дискретных состояний системы, переходов из одного состояния в другое и вероятностью переходов (рис. 1).
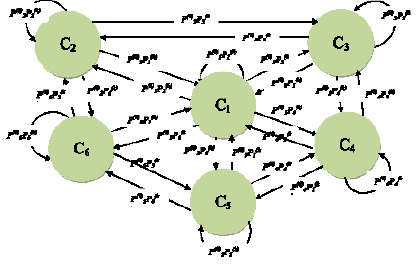
Рис. 1. Орграф системы сохранения качества ПВН у потребителей (эксплуатантов)
Из-за сложности представления и перегруженности рисунка на орграфе отсутствуют переходы С2 С4 , С2 С5,С3 С5 ,С3 С6 , С4 С2 , С5 С2 , С5 С3 , С6 С3 , С4 С6,С6 С4 ,С2 С4 , С2 С4 , С2 С4 , С2 С4 , С2 С4 , что в целом не влияет на смысл и содержание модели ССК в ее динамике как совокупность переходов в свои состояния с различной вероятностью.
Марковская модель ССК представляет собой совокупность следующих шести ее возможных состояний и i-j переходов из одного состояния в другое:
С1 – полное соответствие требованиям (результативность и эффективность системы не менее 95 %);
С2 – неполное соответствие требованиям из-за деятельности поставщика (результативность и эффективность системы не менее 85 %);
С3 – неполное соответствие требованиям из-за действий эксплуатанта (результативность и эффективность системы не менее 85 %);
С4 – неполное соответствие требованиям из-за деятельности сервисного центра (результативность и эффективность системы не менее 85 %);
С5 – полное несоответствие деятельности ССК (результативность и эффективность системы менее 85 %);
С6 – принятие решений для устранения несоответствий в деятельности ССК. Последующая реализация решений – разработка и выполнение необходимых действий в соответствии с принятыми решениями, устранение несоответствий для возвращения системы в исходное состояние (восстановление системы до достижения ее результативности и эффективности значений не менее 95 %).
Вероятность k-го перехода системы из начального состояния i в состояние j и из состояния j в состояние i определяется следующим соотношением [4–6]:
P(k+1) = P(0)T(k+1) , (1)
где k = 1, 2, 3…, n – количество переходов системы из начального состояния, P(0) – значения вероятностей нахождения системы в исходном (соответствующем требованиям, результативном) состоянии, P(k) – значения вероятностей нахождения системы в одном из шести возможных состояний, а Tk – матрица k-го перехода:
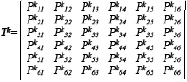(2)
При этом выполняется следующее условие: сумма вероятностей в каждой строке матрицы равна единице:
Р(k)i1+ Р(k)i2 + Р(k)i3 +Р(k)i4 +Р(k)i5 + Р(k)i6 = 1.
В описании состояний и переходов между ними использованы следующие обозначения.
Вероятность Рi(0) – вероятность того, что в настоящее время система находится в одном из состояний Сi (i = 1,2,3,4,5,6);
Р(0)iРj(k) – вероятность того, что в результате k-го перехода произойдет изменение состояния системы от Сi к состоянию Сj,. Так, например, Рi(1) – вероятность того, что в результате деятельности системы в течение первого по счету от ее исходного состояния этапа деятельности (перехода) она окажется в одном из шести своих возможных состояний.
Рi(1) – вероятность того, что в результате первого этапа своей деятельности система находится в одном из своих шести состояний Сi.
Вероятность перехода системы от одного из состояний Сi к одному из состояний Сj определяется суммой произведений соответствующих вероятностей нахождения системы в исходном и следующим за переходом состоянии [4–6]:
Рi(1) = Р(0)1Р1i + Р(0)2Р2i +P(0)3P3i +…+ P(0)nPni,. (3)
По формулам (1)–(3) могут быть рассчитаны как вероятность сохранения своего исходного состояния, так и вероятность его изменения при выполнении своих функций. Последовательность перехода и изменения состояний системы задается номером перехода k.
Анализ деятельности системы сохранения качества продукции на ее марковской модели
В деятельности ССК номер перехода k ассоциируется с временным интервалом в функционировании системы, в течение которого она должна, сохраняя свое исходное состояние, результативность и эффективность, поддерживать качество продукции у эксплуатанта на заданном уровне. Исходная вероятность для каждого из возможных состояний системы устанавливается экспертным методом с учетом всех факторов, влияющих на ее деятельность. Основаниями для достоверной и обоснованной экспертной оценки исходной вероятности нахождения системы в одном из своих состояний являются ее организационная и функциональная структура, стабильность и результативность процессов, а также методы обеспечения ее устойчивости [1–3]. Устойчивость системы обеспечивается мониторингом процессов, менеджментом рисков, управлением изменениями и онлайн- аудитом деятельности удаленных сервисных центров [16].
Так, например, если вероятность полного соответствия системы С1 требованиям перед началом ее функционирования С1 оценивается как Р1(0) = 0,98, вероятность неполного соответствия по вине разработчика (поставщика) С2 – как Р2(0) = 0,001, вероятность неполного соответствия по вине эксплуатанта (потребителя) С3 – как Р3(0) = 0,003, вероятность неполного соответствия по вине сервисного центра С4 – как Р4(0) = 0,006, вероятность полного несоответствия деятельности системы – как Р5(0) = 0,001, а вероятность потребности в устранении несоответствий в деятельности системы С6 – как Р6(0) = 0,008, то описание начального состояния системы принимает вид:
Р(0)= (Р1(0), Р2(0),Р3(0),Р4(0), Р5(0), Р6(0)) =
= (0,98; 0,001; 0,003; 0,006; 0,002; 0,008) (4)
Начальный вектор состояния для рассматриваемого примера может быть записан в матричном виде:
(5)
Матрица перехода между состояниями системы включает в себя значения вероятностей, их характеризующих и определяемых с учетом влияющих на систему факторов: данных о стабильности параметров и эксплуатационных характеристик ПВН при эксплуатации, а также о стабильности и результативности ее участников: организации – поставщика (изготовителя) ПВН, эксплуатанта (потребителя) и сервисного центра.
Так, в оценке вероятности изменения состояний системы в рассматриваемом случае учтено, что с большей вероятностью (P_11^1) система сохраняет свое исходное устойчивое результативное состояние (С1) благодаря всем включенным в управление системой средствам (менеджменту рисков, управлению изменениями, виртуальному аудиту и др.). Со значительно меньшей вероятностью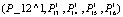 
возможны переходы и в другие состояния (первая строка матрицы).
Вероятность (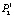
) перехода системы, оказавшейся в состоянии С2 (неполное соответствие по вине поставщика), в состояние С1 (возвращение в нормальное рабочее состояние) высока благодаря мониторингу процессов в системе и своевременному реагированию на возможные несоответствия. По этой причине значительно менее вероятно (
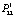= 0,01) для системы оставаться в состоянии неполного соответствия по вине поставщика (С2), а также развивать наметившееся отклонение в деятельности от заданного состояния (С1), что оценивается вероятностью перехода от состояния С2 к состоянию С3 (неполное соответствие по вине эксплуатанта). Вероятность такого сценария ухудшения деятельности системы невелика, но существует (
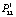- = 0,003). Вероятность (
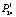- = 0,004) продолжения снижения результативности по вине сервисного центра С4 предусматривает и такой исход событий в деятельности системы. Одновременное несоответствие всех участников и в итоге переход с вероятностью 
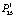= 0,004 в состояние С5 (полное несоответствие системы установленным требованиям) завершает эту траекторию ухудшения деятельности системы. За этим должен последовать переход к С6 – принятие решений для устранения несоответствий в деятельности ССК и возвращение вследствие этого в состояние С1. Высокая вероятность этого перехода оценивается соответственно как 
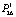= 0,97.
Переход из состояния С3 (неполное соответствие по вине эксплуатанта) к исходному состоянию С1 возможен с вероятностью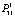 
= 0,95, а к состоянию С2 , т.е. к несоответствию по вине поставщика, – со значительно меньшей вероятностью 
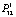= 0,001. Вероятность дальнейшего снижения результативности системы еще и по вине эксплуатанта (потребителя ПВН) – переход С3С4 – оценивается как 
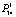= 0,001. Переход С3С5 к полному несоответствию системы С5 возможен с вероятностью 
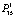= 0,003, а переход к состоянию принятия решений С6 возможен с вероятностью 
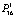= 0,04.
Подобным образом оценивается и устанавливается вероятность переходов из других возможных состояний системы – С4, С5, С6.
С учетом этого матрица перехода системы из состояния С1 для рассматриваемого примера принимает вид:
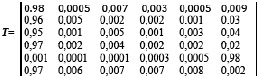(6)
Вероятностная динамика первого перехода (этапа) ССК на ее модели в виде наиболее значащих переходов в цепи Маркова графически представлена на рис. 2. Из-за сложности и перегруженности рисунка на орграфе, как и на рис. 1, отсутствуют переходы С2 С4, С2 С5,С3С5 ,С3С6 , С4С2 , С5С2 , С5С3 , С6С3 , С4С6,С6С4 ,С2 С4 , С2 С4 , С2 С4 , С2 С4 , С2 С4 .
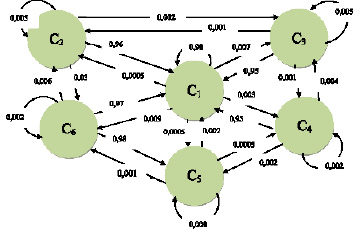
Рис. 2. Орграф системы сохранения качества ПВН у потребителей (эксплуатантов)
Наибольший интерес в анализе системы представляет оценка динамики изменения вероятности сохранения системой своего исходного состояния С1 на последующих этапах своей деятельности. Сохранение системой своего исходного состояния является критерием ее устойчивости. Расчет по формулам (3)–(6) для первого перехода (этапа) дает следующий результат:
(7)
Результаты вычисления показывают, что для системы после первого этапа своей деятельности вероятность остаться в исходном состоянии составляет 0,9778, перейти во второе состояние – 0,0,00056, в третье – 0,0030 и так далее, как следует из (7). Вероятность, с какой система окажется в том или ином состоянии из шести возможных после второго этапа (перехода), вычисляется так же:
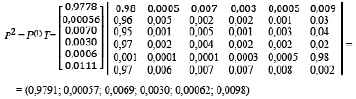(8)
Вероятность изменения системой своего состояния на третьем этапе вычисляется так же и дает следующие результаты:
(9)
Динамика изменения состояния системы по расчету вероятности на четвертом этапе также показывает высокую вероятность сохранения системой своего исходного состояния:
(10)
Незначительные изменения показывают результаты оценки распределения вероятности состояний системы на пятом этапе, что в целом свидетельствует об устойчивости системы и стабильности результатов ее деятельности в рассматриваемом примере:
(11)
На представленном примере показана возможность применения модели для прогнозирования деятельности системы сохранения качества продукции на стадии ее эксплуатации, сопоставления прогнозов с результатами деятельности системы, оценки ее устойчивости, разработки и реализации соответствующих управленческих решений [16].
Оценка вероятности таких переходов и динамики изменения вероятности сохранения исходного (результативного) состояния системы с помощью представленной модели позволит обоснованно разрабатывать и принимать управленческие решения для устойчивого ее функционирования и, как следствие, сохранения качества эксплуатируемой ПВН.
Заключение
Прогнозирование деятельности с помощью представленной модели ССК по ее известному состоянию позволит обоснованно разрабатывать и предпринимать соответствующие действия для обеспечения ее эффективности и выполнения своих функций.
Результат марковского анализа ССК – оценка вероятности того, что система находится в любом из возможных ее состояний, и анализ вариантов соответствующих решений для изменения состояний системы и возвращения ее в исходное состояние для обеспечения стабильности ее деятельности и качества обслуживаемой продукции у эксплуатанта.
Место и роль разработанной модели в управлении ССК, обеспечении ее устойчивости и сохранении качества эксплуатируемой продукции иллюстрирует рис. 3.
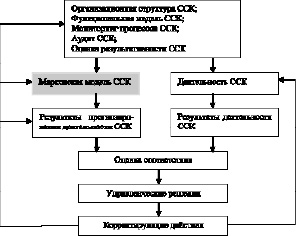
Рис. 3. Роль и место марковской модели ССК в обеспечении устойчивости системы и сохранении качества продукции при ее эксплуатации и применении
Обратная связь – корректирующие действия, реализующие управленческие решения, – обеспечивает как результативность деятельности системы, так и адекватность ее марковской модели своевременным внесением изменений в экспертные оценки вероятности нахождения системы в ее состояниях и переходах между ними.