В настоящее время реализацию таких глобальных отечественных проектов, связанных с освоением природных богатств, расположенных на шельфе Северного Ледовитого океана, невозможно представить без использования низкоорбитальных систем спутниковой связи (НССС). Однако по мере увеличения числа группировок НССС возрастает вероятность навязывания приемнику спутниковой связи, который располагается на необслуживаемом объекте управления (НОУ), ретрансляционной помехи. В качестве такой помехи выступает ранее перехваченный правильный сигнал управления, который передавался с космического аппарата (КА) приемнику НОУ. Чтобы предотвратить попытку навязывания перехваченного сигнала в работе [1], предлагается использовать систему опознавания КА. Для обеспечения высокой скорости определения статуса спутника в работах [2, 3] предлагается реализовать протоколы аутентификации с использованием параллельных кодов системы остаточных классов (СОК). Однако избыточные коды СОК можно также применять для коррекции ошибок, которые могут возникнуть при вычислениях в протоколах аутентификации. Для достижения данной цели коды СОК используют позиционно-интервальную характеристику (ПИХ). Поэтому модификация алгоритма вычисления позиционной интервальной характеристики модулярных кодов для коррекции ошибок является актуальной задачей.
Основным достоинствам кодов СОК является параллельное выполнение модульных аддитивных и мультипликативных операций [4, 5]. Высокая скорость достигается за счет отсутствия обмена промежуточными результатами между основаниями СОК. Тогда ошибка, возникшая в остатке по одному основанию, не будет оказывать влияния на другие остатки кода СОК. Это свойство используется при построении избыточных модулярных кодов, в которых для коррекции ошибочного остатка необходимо вычислить позиционно-интервальную характеристику.
Целью работы является снижение схемных затрат на коррекцию ошибочного остатка СОК за счет модификации алгоритма вычисления ПИХ.
Материалы и методы исследования
Основные принципы построения кодов СОК достаточно полно раскрыты в работах [4–6]. В коде СОК кодовая комбинация представляет собой кортеж остатков:
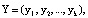 (1)
(1)
где 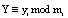 ; mi – основание кода СОК;
; mi – основание кода СОК; 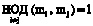 ;
; 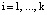 .
.
Произведение оснований кода СОК определяет размер рабочего диапазона:
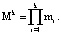 (2)
(2)
Так как коды СОК представлены в алгебраической системе «кольцо», то справедливо:
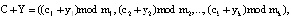 (3)
(3)
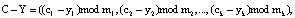 (4)
(4)
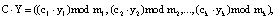 (5)
(5)
где 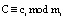 ;
; 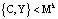 ;
; 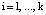 .
.
В протоколе аутентификации [3], который обеспечивает минимальное время опознавания КА за счет кода СОК, используются: W – секретный ключ КА, а также числа С и В для генерации и проверки времени применения n-го сеансового ключа С(n) и B(n), где 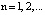 . Протокол представлен в таблице.
. Протокол представлен в таблице.
Протокол аутентификации в коде СОК
|
Ответчик |
Запросчик |
|
|
Секретные параметры в СОК
|
m1,…., mk – модули
|
|
|
|
Исходный статус КА |
|
|
|
Изменение секретных параметров протокола |
|
|
|
Измененный статус |
|
|
Вопрос |
|
|
|
Окончание таблицы |
||
|
Ответчик |
Запросчик |
|
|
|
Вычисляются ответы |
|
|
Проверка ответов |
|
|
Использование модулярных кодов позволяет повысить скорость проводимых вычислений. В работе [5] показано, что для выполнения операции умножения двух 128-битовых операндов максимально требуется 7 CPU Clock Cycles (тактов центрального процессора). Если исходные данные представить в виде 4×32бит, то потребуется 5 тактов CPU Clock Cycles, что в 1,4 раза меньше. Таким образом, очевидно, что применение модулярных кодов позволяет сократить время на опознавание спутника.
Для построения кодов СОК, способных исправлять ошибки в одном остатке, используются два контрольных основания [6–9], для которых истинно неравенство:
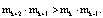 (6)
(6)
В результате получается полный диапазон кода СОК:
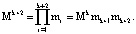 (7)
(7)
Тогда комбинация кода СОК считается разрешенной, если выполнено условие:
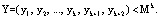 (8)
(8)
Для проверки условия (8) можно использовать обратное преобразование из СОК в позиционный код (СОК-ПК) с использованием Китайской теоремы об остатках (КТО):
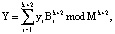 (9)
(9)
где 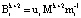 – ортогональный базис для кода СОК, состоящего из k+2 оснований;
– ортогональный базис для кода СОК, состоящего из k+2 оснований; 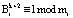 ; ui – вес ортогонального базиса;
; ui – вес ортогонального базиса; 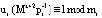 ;
; 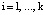 .
.
Условие (8) показывает, что для исправления ошибочного остатка по одному из оснований необходимо определить позицию числа 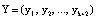 относительно рабочего диапазона. Поэтому для достижения поставленной цели в кодах СОК используются позиционно-интервальные характеристики. Непозиционные избыточные коды СОК характеризуются многовариантностью по использованию ПИХ. В работе [8] для исправления ошибки в одном основании предлагается использовать метод проекции, в котором поочередно из избыточной комбинации СОК удаляются остатки. Полученную комбинацию переводят в позиционный код и сравнивают с Mk. Условие (8) будет выполнено только при удалении ошибочного остатка. В качестве недостатка метода проекции можно отметить последовательный характер определения ошибочного остатка. Кроме того, необходимо выполнять перевод СОК-ПК при изменяющемся кортеже оснований, что требует пересчета ортогональных базисов для выполнения (9). В работе [9] предлагается использовать вычисления следа числа. Для определения ошибочного остатка необходимо из кодограммы СОК последовательно в течение k итераций вычитать константы нулевизации. Если код СОК не содержит ошибки, то в конечном результате должна получиться нулевая комбинация. В противном случае вычисленные остатки
относительно рабочего диапазона. Поэтому для достижения поставленной цели в кодах СОК используются позиционно-интервальные характеристики. Непозиционные избыточные коды СОК характеризуются многовариантностью по использованию ПИХ. В работе [8] для исправления ошибки в одном основании предлагается использовать метод проекции, в котором поочередно из избыточной комбинации СОК удаляются остатки. Полученную комбинацию переводят в позиционный код и сравнивают с Mk. Условие (8) будет выполнено только при удалении ошибочного остатка. В качестве недостатка метода проекции можно отметить последовательный характер определения ошибочного остатка. Кроме того, необходимо выполнять перевод СОК-ПК при изменяющемся кортеже оснований, что требует пересчета ортогональных базисов для выполнения (9). В работе [9] предлагается использовать вычисления следа числа. Для определения ошибочного остатка необходимо из кодограммы СОК последовательно в течение k итераций вычитать константы нулевизации. Если код СОК не содержит ошибки, то в конечном результате должна получиться нулевая комбинация. В противном случае вычисленные остатки 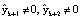 . По величине полученного следа можно однозначно определить и исправить ошибочный остаток. Однако данный алгоритм не может быть реализован параллельно, так выбор констант нулевизации зависит от результата, полученного на предыдущей итерации.
. По величине полученного следа можно однозначно определить и исправить ошибочный остаток. Однако данный алгоритм не может быть реализован параллельно, так выбор констант нулевизации зависит от результата, полученного на предыдущей итерации.
Устранить данные недостатки можно с помощью алгоритма вычисления ПИХ, приведенного в работе [10]. Однако он обладает недостатком – вычисления ПИХ проводятся по большему модулю 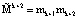 , что увеличивает схемные затраты. Для устранения данного недостатка проведем его модификацию.
, что увеличивает схемные затраты. Для устранения данного недостатка проведем его модификацию.
Для проверки выполнения условия (8) найдем ПИХ, используя выражение:
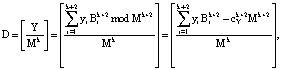 (10)
(10)
где [ ] – целая вычисленного частного; 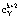 – позиционная характеристика ранг числа Y, которая определяет количество переходов за Mk+2 при выполнении перевода СОК-ПК.
– позиционная характеристика ранг числа Y, которая определяет количество переходов за Mk+2 при выполнении перевода СОК-ПК.
В работе [7] доказано, что ортогональные базисы для полного 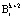 и рабочего
и рабочего 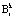 диапазонов подобны. Следовательно, для них справедливо:
диапазонов подобны. Следовательно, для них справедливо:
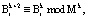 (11)
(11)
где 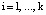 .
.
На основе свойства (11) справедливо равенство:
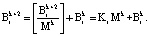 (12)
(12)
В этом случае выражение (10) можно представить:
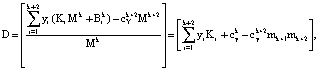 (13)
(13)
где 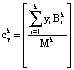 – ранг числа Y в коде СОК, состоящего из k оснований.
– ранг числа Y в коде СОК, состоящего из k оснований.
Позиционно-интервальная характеристика, определяемая (10), может принимать значения от 0 до 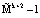 . Значит, используя изоморфизм, порожденный КТО, можно перейти от вычислений по одному модулю
. Значит, используя изоморфизм, порожденный КТО, можно перейти от вычислений по одному модулю 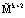 к параллельным вычислениям по контрольным основаниям mk+1, mk+2. Тогда:
к параллельным вычислениям по контрольным основаниям mk+1, mk+2. Тогда:
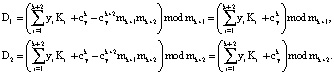 (14)
(14)
Для выполнения (13) используется LUT-таблица, содержащая 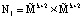 ячеек памяти запоминающей матрицы. При использовании модифицированного алгоритма вычисления ПИХ потребуется
ячеек памяти запоминающей матрицы. При использовании модифицированного алгоритма вычисления ПИХ потребуется 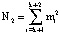 . Очевидно, что N2 < N1.
. Очевидно, что N2 < N1.
Результаты исследования и их обсуждение
Пусть имеем информационные модули m1 = 7, m2 = 17, m3 = 19 и два контрольных m4 = 29, m5 = 31. Диапазоны кода СОК: рабочий Mk = 2261, полный Mk+2 = 2032639, контрольный 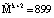 . Для данных оснований получаем ортогональные базисы:
. Для данных оснований получаем ортогональные базисы:
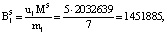
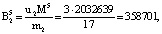
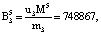
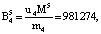
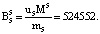
Представим их согласно выражению (12):
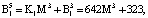
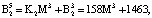
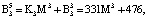
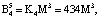
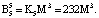
Пусть на вход блока вычисления ПИХ подается код 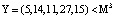 . Тогда ранг числа Y по информационным модулям равен:
. Тогда ранг числа Y по информационным модулям равен:
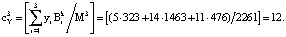
Тогда ПИХ равна:

Так как ПИХ равна нулю, то комбинация является разрешенной, т.е. Y < Mk.
Пусть в процессе выполнения протокола аутентификации произошла ошибка и на вход блока ПИХ поступила комбинация 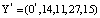 . Тогда ранг числа Y* равен:
. Тогда ранг числа Y* равен:
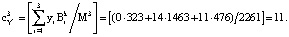
Тогда ПИХ равна
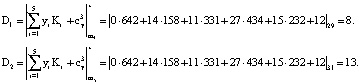
Получили: ПИХ равен 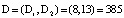 ), где
), где 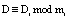 , i = 4,5.
, i = 4,5.
Воспользуемся алгоритмом вычисления ПИХ [10]. Получаем:
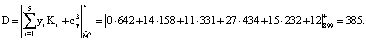
Для этого значения ПИХ вектор ошибки Δкорр = (2,0,0,0,0). Коррекция дает:
Y = Y* – Δкорр = 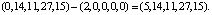
Модифицированный алгоритм вычисления ПИХ показал аналогичный результат по сравнению с прототипом, для которого требуется 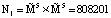 ячеек памяти LUT-таблицы. При этом для модифицированного алгоритма вычисления ПИХ используется
ячеек памяти LUT-таблицы. При этом для модифицированного алгоритма вычисления ПИХ используется 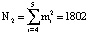 ячеек памяти запоминающей матрицы LUT-таблицы. Очевидно, что поставленная цель, направленная на снижение схемных затрат, достигнута.
ячеек памяти запоминающей матрицы LUT-таблицы. Очевидно, что поставленная цель, направленная на снижение схемных затрат, достигнута.
Заключение
В статье показан протокол аутентификации спутника, реализованный в коде СОК. Применение данного кода за счет параллельных вычислений позволяет не только уменьшить время на опознавание КА, но и корректировать ошибки, которые могут возникнуть в процессе работы системы «свой – чужой» для НССС. С целью снижения схемных затрат на реализацию запросно-ответной системы была проведена модификация алгоритма вычисления ПИХ. Поставленная цель достигнута благодаря изоморфизму Китайской теоремы об остатках. В статье рассмотрен пример реализации модифицированного алгоритма вычисления ПИХ. Полученные результаты совпали с результатами прототипа, для которого требуется N1 = 808201 ячеек памяти LUT-таблицы. При этом для модифицированного алгоритма вычисления ПИХ используется N2 = 1802 ячеек памяти запоминающей матрицы LUT-таблицы. Очевидно, что поставленная цель, направленная на снижение схемных затрат, достигнута.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-37-90009.




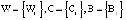
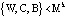
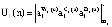
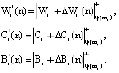
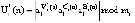
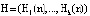
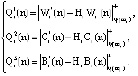
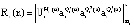
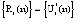 – КА «свой»
– КА «свой»