Задача формирования изображений (визуализации) на основе трехмерной модели является одной из важнейших проблем в области компьютерной графики, компьютерной анимации и в системах автоматизированной подготовки производств (САПР). На сегодняшний день существует множество алгоритмов визуализации, которые основаны на различных подходах к получению результирующего изображения, которые можно разделить на следующие группы:
– проецирование (сюда относится алгоритм растеризации);
– трассировка (прямая и обратная трассировка лучей, трассировка пути).
В первой группе алгоритмов осуществляется проецирование объектов сцены на экран наблюдения; во второй группе алгоритмов используются различные подходы проведения отдельных лучей между сценой и экраном, на котором формируется изображение. Но в каждом из механизмов получения изображений используется физическая модель сцены и физическая модель луча, поэтому каждый из этих методов требует существенных вычислительных ресурсов для своей работы.
Специализированные вычислительные системы позволяют решить задачу визуализации изображений за приемлемое время и обладают существенными преимуществами перед вычислительными системами общего назначения. Подобные системы могут строиться на принципах параллелизма и повышения степени специализации вычислительных узлов для решения именно задач обработки изображений. Графические процессоры позволяют за счет более простой структуры осуществлять параллельную обработку большого количество элементов изображений, в частности для компьютерных игр, где преобразование осуществляется в режиме реального времени. Во многих областях нет требования к получению итогового изображения в режиме реального времени (например, в анимации или САПР); в таких случаях могут использоваться многоядерные процессоры, а также распределенные системы.
В настоящее время большинство вычислительных ресурсов сосредоточено во встраиваемых системах, к которым можно отнести также объекты Интернета вещей (ИВ, IoT – Internet of Things), представляющие собой множество вычислительных узлов гетерогенной структуры.
Спецификой вычислительной системы на основе ИВ (Интернета вещей) является:
– гетерогенность узлов, высокое разнообразие технологического стека;
– использование беспроводных сетей;
– наличие нескольких режимов работы у встроенного микропроцессора.
В работах [1–3] продемонстрирована возможность построения вычислительной системы на основе объектов ИВ.
В данной работе приводится подход по реализации алгоритма трассировки лучей для получения изображений по модели сцены. Данный подход реализован с использованием распределенной вычислительной системы на основе объектов ИВ.
Материалы и методы исследования
1. Трассировка лучей
В основе трассировки лучей (Ray tracing) лежит идея отслеживания взаимодействия отдельных лучей с поверхностями объектов [4]. Сами объекты и лучи описываются в виде математических моделей. Наборы моделей объектов, изображения которых необходимо получить, формируют собой сцену. Отраженное освещение от объектов сцены проходит к точке обзора (камера), где расположен наблюдатель. Наблюдатель не может видеть всей сцены, а только её часть, которая видна в так называемое окно просмотра (viewport). Камера (наблюдатель), окно просмотра и сцена являются элементами схемы трассировки лучей.
Элементы схемы трассировки лучей показаны на рис. 1.
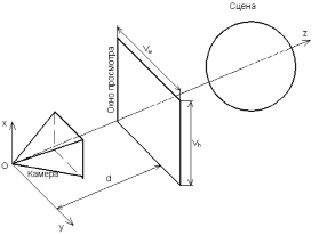
Рис. 1. Элементы схемы трассировки лучей
Существует несколько подходов к трассировке лучей:
- прямая трассировка, когда рассматривается луч, идущий от объектов сцены до камеры;
- обратная, когда рассматривается луч, идущий от камеры к объекту сцены.
В первом случае возможна более глубокая проработка изображения, так как позволяет проработать взаимное влияние лучей друг на друга (например, отраженный от одного объекта сцены, свет влияет на освещение других объектов сцены), даже если в итоге не все лучи попадают в камеру. Данный подход требует больших вычислительных затрат.
Второй подход требует меньше вычислений: так, отслеживаются только лучи, которые попадают в камеру. Необходимо отметить, что при обратной трассировке луча также можно учитывать влияние лучей друг на друга, но при этом можно задавать степень влияния лучей друг на друга, в результате чего получаемые изображения могут иметь различную степень «реалистичности».
Для реализации алгоритма обратной трассировки лучей использована схема, показанная на рис. 1. На схеме имеются следующие допущения:
- положение камеры фиксировано в начале координат – точка O(Ox, Oy, Oz) = O(0, 0, 0);
- ориентация камеры фиксирована вдоль оси Oz;
- окно просмотра расположено перпендикулярно оси ориентации камеры и расположено на расстоянии d от камеры;
- окно просмотра имеет размеры Vw и Vh, а его стороны параллельны осям Ox и Oy.
Область видимости (field of view) определяется размером окна просмотра и расстоянием до камеры. Холст изображения сопоставляется с окном просмотра. Сам холст состоит из элементов изображений – пикселов (pixel – picture element), размер холста в пикселах определяет разрешение получаемого изображения. На окно просмотра наносится сетка, ячейки которой ставятся в соответствие с каждым элементом изображения.
Таким образом, можно описать алгоритм получения изображения трехмерного объекта в общем виде:
Шаг 0. Начало алгоритма.
Шаг 1. Разместить камеру и окно просмотра в необходимых местах.
Шаг 2. Для каждого пиксела холста выполнить:
Шаг 2.1. Определить квадрат сетки окна просмотра, который соответствует данному пикселу.
Шаг 2.2. Определить цвет, который виден через квадрат сетки.
Шаг 2.3. Закрасить пиксел полученным цветом.
Шаг 3. Конец алгоритма.
Как видно из алгоритма, каждый пиксел не зависит от других пикселов, подобная задача имеет высокую степень распараллеливания и может быть решена на распределенной вычислительной системе.
2. Распределенная вычислительная система на основе объектов Интернета вещей
Задача по трассировке лучей заключается в распределении заданий по узлам распределенной вычислительной системы. В роли такой системы может выступать распределенная система на основе объектов ИВ, вычислительный процесс в которой реализован на основе машинного обучения с подкреплением [5], в частности на основе алгоритма многорукого бандита.
Рис. 2. Схема взаимодействия агента и окружающей среды
Структура вычислительной системы на основе объектов ИВ может быть представлена взаимодействием агента и окружающей среды (рис. 2). В качестве среды в данной инфраструктуре выступают вычислительные узлы, построенные на основе объектов ИВ. Характеристики окружающей среды определяются числом вычислительных узлов и их характеристиками (пропускная способность линий связи, частота и режим работы процессора, объем памяти и т.п.).
В качестве агента выступает реализуемый на центральном управляющем узле распределительный узел, который выполняет разделение исходного алгоритма на относительно независимые задания, которые будут затем отправлены на вычислительные узлы. Несмотря на то, что спецификой распределенной вычислительной системы на основе объектов ИВ является невозможность определения текущего состояния каждого вычислительного узла, распределяющему узлу не требуется строить модель окружающей среды, поскольку он принимает решения на основании реакций (вознаграждений), получаемых от окружающей среды, а также на основании предпринятых ранее действий.
Особенностью алгоритма распределения заданий по вычислительным узлам является его реализация на основе машинного обучения с подкреплением, то есть агент самостоятельно определяет стратегию своего поведения в зависимости от состояния окружающей среды и постоянно адаптируется к ее изменениям.
В алгоритме распределения заданий можно выделить два режима работы:
- режим исследования (exploration), когда алгоритм «пробует» новые действия;
- режим использования (exploitation), когда алгоритм выполняет только те действия, которые могут дать максимальный результат на текущем шаге.
Баланс между режимами исследования и использования определяется параметром ε, где при значении параметра, равном 0, агент не пытается выполнять новые действия, а выполняет только действия, дающие наибольшее вознаграждение (так называемая жадная стратегия). Если параметр равен 1, то алгоритм на каждом этапе случайным образом выбирает новое действие.
Таким образом, можно сформулировать алгоритм решения задачи по трассировке лучей по вычислительным узлам:
Шаг. 0. Начало алгоритма. Распределяющий узел получает характеристики сцены (модели трехмерных объектов), камеры, окна просмотра.
Шаг 1. Задача разбивается на последовательность заданий (окно просмотра разбивается на сетку и каждая её ячейка сопоставляется с пикселом холста).
Шаг 2. Распределяющий узел оценивает состояние вычислительных узлов: определяется вероятность (готовность) каждого вычислительного узла для принятия задания.
Шаг 3. Распределяющий узел в соответствии со значениями вероятностей назначает задания вычислительным узлам, которые дадут максимальное вознаграждение.
Шаг 4. Распределяющий узел отправляет задания на вычислительные узлы.
Шаг 5. Вычислительные узлы выполняют задания и отправляют результаты на распределительный узел, который пересчитывает значения вознаграждения для каждого из вычислительных узлов.
Шаг 6. Если есть еще вычислительные задания, то переход на Шаг 3, иначе – переход на Шаг 7.
Шаг 7. Конец алгоритма.
В соответствие с [1–3] при времени работы алгоритма, стремящемуся к бесконечности, будет получен результат близкий к оптимальному, то есть агент выработает такое поведение с переменчивой средой, что распределенная вычислительная система на основе объектов ИВ не будет иметь отличий от обычной классической параллельной вычислительной системы.
3. Алгоритм трассировки лучей для распределенной системы
Рассмотрим подробнее Шаг 2 алгоритма получения изображения. Также будут использованы указанные ранее допущения на размещение камеры, окна просмотра и их параметров, также для простоты не будет учитываться модель освещения сцены. В качестве сцены будет рассмотрена модель одного объекта – сфера.
Пусть Cx и Cy – координаты пиксела на холсте, тогда переход от координат холста к координатам точки пространства V = (Vx, Vy, Vz) будет определяться следующими уравнениями:
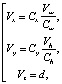(1)
где Cw – ширина холста, Ch – высота холста.
Луч, исходящий от камеры (начала координат), может быть описан следующим параметрическим уравнением:
P = O + t(V – O), (2)
где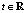 
– некоторое произвольное число, а P – произвольная точка луча.
Лучи, направленные от камеры, проходят через экран и окно наблюдения, пока не столкнутся со сферой, описанной следующим уравнением:
|P – C| = r, (3)
где P – точка на поверхности сферы, C – центр сферы, а r – радиус сферы.
Если в уравнении (2) принять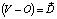 
, а также учесть, что |P – C| – длина вектора 
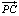, определяемая как корень квадратный из его скалярного произведения на самого себя, то можно получить следующую систему уравнений:
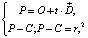(4)
решением которой будет точка пересечения луча со сферой.
Если преобразовать уравнение к виду
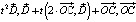, (5)
где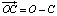 
, а затем совершить замену 
, 
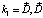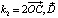и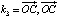 
, то получим квадратное уравнение:
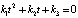, (6)
решением которого будет
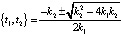. (7)
Таким образом, подставив полученные значения в первое уравнение системы, можно получить точку луча, который пересекается со сферой, при этом необходимо выбирать только значения t > 1, так как именно они соответствуют точкам, расположенным на сцене (при t < 0 точки располагаются за камерой, а при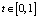 
– между камерой и плоскостью проекции).
Поскольку процедура определения точки пересечения заключается в нахождении корней уравнения (6), которое строится независимо для каждой точки, то для распределения заданий по узлам распределенной вычислительной системы можно выбрать подпрограмму, выполняющую трассировку отдельного луча.
Алгоритм расчета изображений:
Шаг 0. Начало алгоритма.
Шаг 1. O = (0, 0, 0)# Задание координат камеры
Шаг 2. Для каждого пиксела с координатами (x,y) канвы выполнять:
Шаг 2.1. D = КанваКОкну(x,y) # Преобразование координат пиксела канвы к кординатной сетке окна наблюдения
Шаг 2.2. color = Трассировка_луча (O, D, 1, ∞)
Шаг 2.3. НарисоватьПиксел (x, y, color)
Алгоритм подпрограммы вычисления цвета пиксела Трассировка_луча():
Подпрограмма Трассировка_луча (O, D, tmin, tmax):
Шаг 1. Ближайший_t = ∞
Шаг 2. Ближайший_объект = NULL
Шаг 3. Для каждого Объекта сцены:
Шаг 3.1. t1, t2 = ПересечениеЛучОбъект(O, D, объект)
Шаг 3.2. Если t1 в [tmin, tmax] и t1 < ближайший_t
тогда ближайший_t = t1
ближайший_объект = Объект
Шаг 3.3. Если t2 в [tmin, tmax] и t2 < ближайший_t
тогда ближайший_t = t2
ближайший_объект = Объект
Шаг 4. Если ближайший_объект = NULL
тогда вернуть Цвет_белый
иначе вернуть Цвет_объекта
Шаг 5. Конец подпрограммы Трассировка_луча
Алгоритм подпрограммы ПересечениеЛучОбъект:
Подпрограмма ПересечениеЛучОбъект (O, D, сфера):
Шаг 1. с = сфера. центр
Шаг 2. r = сфера. радиус
Шаг 3. OC = O – C
Шаг 4. k1 = скалярноеПроизведение (D, D)
k2 = 2⋅скалярноеПроизведение (OC, D)
k3 = скалярноеПроизведение(OC, OC) – r2
Шаг 5. Дискриминант = k2⋅k2 – 4⋅k1⋅k3
Шаг 6. Если Дискриминант < 0
тогда вернуть ∞,∞
Шаг 7.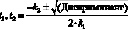 
Шаг 8. Вернуть t1, t2
Шаг 9. Конец подпрограммы ПересечениеЛучОбъект
4. Архитектура системы и экспериментальная установка
Для проведения экспериментов был разработан стенд, состоящий из ряда аппаратных узлов, реализованных на Raspberry Pi, и ряда виртуальных узлов, реализованных на виртуальных машинах. Все устройства соединены между собой с помощью сети: виртуальные узлы посредством виртуальной сети Ethernet, соединенной с помощью моста с физической сетью, а аппаратные устройства подключены непосредственно через точку доступа сети WiFi. Таким образом, все узлы оказываются в одном сегменте сети и могут друг с другом взаимодействовать.
Общее количество вычислительных узлов – 15, из них 10 аппаратных и 5 вирту- альных.
Общая архитектура вычислительной системы представлена на рис. 3.
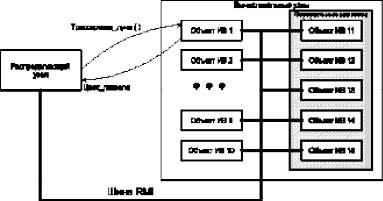
Рис. 3. Архитектура стенда распределенной вычислительной системы на основе объектов ИВ
В качестве распределяющего узла используется персональный компьютер, который подключен к точке доступа WiFi по проводному каналу Ethernet.
При разработке объектов интернета вещей используются стандартизированные цифровые платформы (на базе микропроцессоров ARM, Intel), основанные на использовании стандартных компонентов: микропроцессоры, память, периферийные устройства, порты вводы-вывода. Производителей компонентов достаточно большое количество, и в каждом случае компоненты могут иметь свои несущественные особенности, что приводит к тому, что программы для каждой из платформ не могут быть переносимыми, если реализованы на низкоуровневом языке ассемблера. Именно поэтому для реализации стенда предлагалось использовать языки более высокого уровня – например Си, тем не менее специфика каждой платформы дает о себе знать. Для нивелирования особенностей платформ используется операционная система GNU/Linux: для виртуальных узлов – Ubuntu, для аппаратных узлов – Raspbian.
В качестве языка разработки был выбран язык Java, а для взаимодействия узлов были выбраны технологии платформы Java – RMI (Remote Method Invocation) [6]. Платформа Java позволяет избежать любых возможных проблем в различии электронных компонентов и цифровых платформ. Виртуальная машина Java (JVM) устанавливается на всех устройствах вычислительной платформы ИВ, что позволяет использовать общий переносимый программный код, который будет преобразован в байт-код для выполнения на каждом устройстве.
Результаты исследования и их обсуждение
Для подтверждения работоспособности распределенной вычислительной системы на основе объектов ИВ были проведены следующие эксперименты:
- определение времени решения задачи трассировки в зависимости от количества вычислительных узлов;
- определение времени выполнения одного задания;
- определение зависимости времени выполнения задачи трассировки в зависимости от размера изображения.
Для определения времени решения задачи в зависимости от количества вычислительных узлов был зафиксирован размер канвы изображения в 100х100 пикселов, то есть распределяющий узел формирует последовательность из 10 000 заданий, каждое из которых отправляется на вычислительный узел.
Результаты эксперимента приведены на рис. 4, где видно, что при увеличении количества вычислительных узлов в распределенной вычислительной системе время выполнения задачи снижается. При этом видно, что при двух вычислительных узлах время решения задачи аналогично времени при четырех узлах. Так как при двух узлах алгоритм распределения заданий на основе обучения с подкреплением практически не выполняет свою работу, так как у него всего два узла и времени на выбор узла и пересчета параметров модели не тратится – накладные расходы минимальные, но уже при трех узлах накладные расходы становятся существенны по сравнению со временем обработки задачи, поэтому производительность системы падает, что приводит к увеличению времени выполнения задания. После включения четырех узлов и более накладные расходы на распределение становятся несущественными. Начиная от одиннадцати вычислительных узлов, время решения задачи продолжает уменьшаться, но при этом скорость уменьшения снижается.
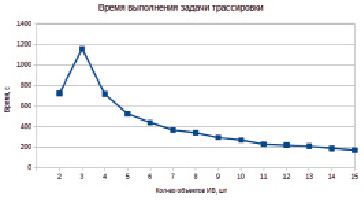
Рис. 4. Время выполнения задачи
Для оценки времени выполнения одного задания также использовалось изображение 100х100 пикселов. Замер выполнения задания выполнялся на распределительном узле, время выполнения, таким образом, включает в себя не только время непосредственной обработки каждого задания на вычислительном узле, но также и время, необходимое для выбора алгоритмом распределения вычислительного узла, а также случаи, когда задание не может быть обработано на том узле, куда оно было направлено, и его необходимо было направить на другой узел для выполнения.
На рис. 5 показана зависимость времени выполнения одного задания от количества вычислительных узлов. Поскольку для двух узлов (как было сказано ранее) накладные расходы минимальны, то можно увидеть, что время исполнения заданий также минимально, так как включает только время непосредственной работы вычислительного узла. При количестве узлов более пяти время выполнения одного задания стабилизируется и начинает приближаться к среднему времени выполнения каждого задания, с учетом времени на накладные расходы. В данном случае можно отметить, что при количестве вычислительных узлов более пяти система находится в стабильном состоянии, то есть время выполнения одного задания не зависит от количества вычислительных узлов.
Для анализа времени выполнения задачи в зависимости от количества заданий была проведена оценка работы алгоритма распределения при обработке изображений от размера 100х100 пикселов до 750х750 пикселов с шагом в 50 пикселов по каждому измерению, при этом количество вычислительных узлов фиксировано десятью. Результаты оценки приведены на рис. 6.
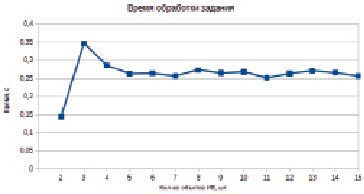
Рис. 5. Время выполнения одного задания
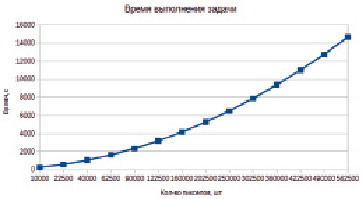
Рис. 6. Время выполнения задачи в зависимости от размера обрабатываемого изображения
Оценка времени выполнения задачи показывает, что при увеличении количества заданий время обработки увеличивается, при этом постепенно время растет быстрее, чем линейно.
Сравнение результатов экспериментов с результатами других исследований [7–10] показывает, что полученные зависимости имеют аналогичный вид и соответствуют зависимостям для обычных параллельных и распределенных вычислительных систем, построенных на основе классических подходов [11, 12], для суперкомпьютерных и облачных систем [13, 14].
В результате проведения эксперимента были построены зависимости общего времени выполнения задачи от количества вычислительных узлов, времени выполнения одного задания на вычислительном узле в зависимости от количества узлов в системе, а также зависимость времени выполнения задачи трассировки луча от количества элементов изображений. Результаты экспериментов показали возможность и эффективность реализации распределенной вычислительной системы на основе объектов ИВ.
Заключение
В работе представлен подход, позволяющий провести построение изображения по модели трехмерного объекта с помощью трассировки луча. В качестве вычислительной была использована распределенная вычислительная система на основе объектов ИВ.
В качестве решаемой задачи была использована задача построения изображений с помощью трассировки лучей. Данная задача имеет высокую степень распараллеливания, так как каждый пиксел изображения формируется независимо от других.
Использование метода распределения заданий по вычислительным узлам на основе машинного обучения с подкреплением позволяет построить распределенную вычислительную систему, в основе которой лежат гетерогенные вычислительные узлы на основе объектов ИВ.