Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Проблематика творческого мышления в области математики привлекает внимание ученых чуть более ста лет, хотя представления о математике как особом виде научного творчества возникли гораздо раньше. Вопрос о собственно математическом творчестве поднял великий Анри Пуанкаре в специальном докладе в 1908 г. и развил Жак Адамар в работе 1945 г., посвященной психологии математического мышления. С точки зрения анализа мыслительных процессов этой проблемой занимались гештальт-психологи. Современное понимание математического творчества и его характеристик нашло отражение в работах голландского математика Гонтрана Эрвинка [1] и его последователей [2]. Настоящая статья затрагивает более узкую тему педагогического творчества в преподавании математики.

Педагогическое творчество университетских математиков обычно рассматривается как средство повышения мотивации студентов. Много работ в аспекте мотивации посвящено средствам формирования творческого подхода в преподавании математики. Среди форм организации учебного процесса, ориентированного на математическое творчество, основными считаются элективные курсы, способствующие повышению интереса студентов к изучению математики. Среди способов проведения занятий выделяются метод проектов, кейс-технологии, а также активные и коллективные методы обучения, в частности квест-технологии. Наконец, содержание занятий по математике, способствующих формированию творческого подхода, преимущественно основывается на так называемых открытых задачах [3; 4], синонимами или близкими терминами для которых служат некорректно поставленные задачи [5] или плохо структурированные задачи [6]. Другой вид творческих заданий – задачи, приводящие к намеренно созданным противоречиям [7]. Главный недостаток всех подобных заданий состоит в том, что для их выполнения требуется достаточно много времени, которого не хватает при массовом высшем образовании.

Авторам не удалось найти работы, в которых исследователи рассматривают педагогическое творчество математиков в качестве одного из механизмов противодействия академической нечестности. Поскольку академическая нечестность приобрела в современном образовании массовый характер [8; 9], очевидно, что идет поиск способов предотвращения ее проявлений. Имеются рекомендации общего характера по предотвращению академической нечестности с помощью внедрения творческих заданий [10], варьирования формулировок открытых вопросов в тестах [11]. В то же время очевидно, что существует необходимость использовать творческий потенциал вузовских математиков для противодействия проявлениям академической нечестности студентов.

Преподаватели университетских математических курсов столкнулись с нарастающим количеством случаев проявления академической нечестности с начала 2000-х гг. В это время появились computer aided systems (CAD) и многочисленные интернет-сервисы для быстрого решения математических задач. Самые известные из таких сервисов – WolframAlpha, Slader, Symbolab, Desmos и Photomath [12]. С каждым годом эти системы и сервисы становятся все совершеннее, используют технологии, связанные с искусственным интеллектом. Например, они без труда расшифровывают рукописный текст. Преподаватели математики, разумеется, ищут способы противодействия этой форме академической нечестности, предлагая задания, на которые не могут дать корректные ответы сервисы, подобные WolframAlpha. Обмен идеями происходит и на специализированных блогах, например Mathematics Educators Stack change или Hacker News. Другой вариант списывания – использование человеческих ресурсов через коммуникаторы. Студент передает задание друзьям либо небескорыстным «помощникам», получая в ответ готовое решение. Поскольку решение с помощью коммуникаторов требует значительно большего времени для выполнения заданий, такому варианту проявления академической нечестности можно противостоять, ограничивая время выполнения студентами контрольных мероприятий.

Некоторые расхождения в оценке математиками проявлений академической нечестности возникают вследствие различной трактовки самого понятия «cheating». Эта неоднозначность зависит от того, какие именно действия данный преподаватель считает нелегальными. Некоторые математики не разрешают студентам пользоваться любыми материалами, даже собственными конспектами, требуя, например, знания на память элементарных интегралов или формул для вычисления градиента. Другие позволяют читать учебные пособия и другие материалы на бумажных носителях. Мы приводим дальнейшее рассмотрение с позиций «либерального» преподавателя, запрещающего студентам лишь работу с электронными помощниками и любыми коммуникаторами.

Цель исследования – выявить типы заданий, удовлетворяющих двум требованиям. Во-первых, в этих заданиях используются творческие находки преподавателей, препятствующие проявлениям академической нечестности. Во-вторых, рассматриваемые задания не требуют от студентов слишком много времени для решения.

Материалы и методы исследования

На основании изучения мнений математиков в сети, устного общения с коллегами и анализа немногочисленных литературных источников авторы выделили некоторые типы заданий, которые университетские преподаватели математики используют для противодействия академической нечестности студентов. Мы сгруппировали задания по разделам курса математического анализа, имея в виду уровень первого года обучения российского вуза. Мы также прокомментировали все задания, по возможности обозначая их источник, если задание не является традиционным, а также наличие творческого подхода к их разработке и перспективы применения против проявлений академической нечестности. Кроме того, мы оценили группы направлений подготовки бакалавров, для которых применение тех или иных типов заданий было бы наиболее эффективным не только в аспекте предотвращения академической нечестности, но и как средства формирования требуемых компетенций.

Тема «Введение в математический анализ» («Пределы»)

Задание 1. Найти предел выражения

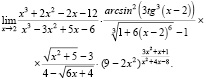
Подобные задания использовались на заре массового проявления студентами академической нечестности, когда главным «помощником» студентов был CAS. Задание включает слишком много символов для набора вручную, возможно, плохо отображается при фотографировании. Задание является традиционным, но творческим. Главный недостаток задания состоит в том, что оно требует большого времени для выполнения студентами, не использующими списывание. Таким образом, наказывая нечестных студентов, можно существенно занизить оценки честным студентам. Также преподаватель тратит слишком много времени на проверку задания. Авторы рекомендуют предлагать такие задания только студентам физико-математических направлений подготовки.

Задание 2. Найти значение параметра α, при котором значение предела равно -2:

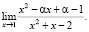
Источник – [13]. Задание является нетрадиционным, творческим. Авторы рекомендуют предлагать такие задания преимущественно студентам физико-математических направлений подготовки.

Задание 3. Сконструировать неопределенное выражение [0/0] при x → 5.

Источник – [13]. Задание является нетрадиционным, творческим. Главным достоинством задания является то, что интернет-платформы и сервисы пока не продуцируют математические объекты по описаниям. Кроме того, честные студенты могут решить задание очень быстро. Главный недостаток задания состоит в его обусловленности контекстом и трактовкой преподавателя. Весьма вероятно, что студенты будут действовать в рамках приведенных на занятиях образцов. Таким образом, являясь продуктом творчества преподавателей, это задание может не дать ожидаемого творческого эффекта в случае пассивности студентов. Авторы рекомендуют предлагать такие задания преимущественно студентам физико-математических направлений подготовки.

Задание 4. Дан график функции (рис. 1). Найти односторонние пределы в точках разрыва и пределы на ±∞.

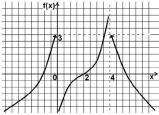
Рис. 1. Односторонние пределы (задание 4)

Собственный пример авторов. Задание является нетрадиционным, творческим. Главное достоинство задания состоит в том, что интернет-сервисы пока не справляются с графической информацией подобного рода. Другое важное преимущество задания состоит в том, что честные студенты могут решить задание очень быстро. Авторы рекомендуют предлагать задание студентам всех направлений подготовки.

Задание 5. Изобразить график функции, имеющий предел -∞ на -∞; предел -∞ на +∞; а также односторонние пределы +3 и -∞ при x = 0; односторонние пределы +∞ и +3 при x = 4.

Собственный пример авторов. Задание является нетрадиционным, творческим. Достоинства и недостатки такие же, как в задании 3. Авторы рекомендуют предлагать такие задания преимущественно студентам физико-математических направлений подготовки.

Тема «Дифференциальное исчисление функции одной переменной» («Производные»)

Задание 6. Найти производную функции

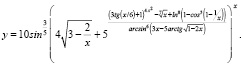
Задание является традиционным для вузовских математиков, нетворческим. Достоинства и недостатки такие же, как и для задания 1. Кроме того, ответ получается слишком громоздким, неудобным для проверки. Авторы рекомендуют предлагать такие задания только студентам физико-математических направлений подготовки, причем преимущественно для самостоятельной работы, а не на контрольных мероприятиях.

Задание 7. Найти знаки первой и второй производных на интервалах (рис. 2).

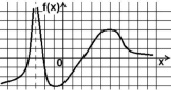
Рис. 2. Возрастание/убывание, выпуклость/вогнутость (задание 7)

Задание является традиционным, но творческим. Достоинства задания такие же, как и для задания 4. Многие коллеги считают это задание слишком простым, не соответствующим университетскому уровню преподавания математики, однако опыт авторов показывает, что полностью правильно выполняют задание не более 60 % студентов. Авторы рекомендуют предлагать такие задания студентам всех направлений подготовки, за исключением физико-математических.

Задание 8. Изобразить график функции, возрастающей на интервале от -∞ до -3, имеющей бесконечный разрыв при x = –3; далее убывающей на интервале от -3 до -1; далее возрастающей на интервале от -1 до 5 и убывающей на интервале от 5 до +∞. При x = –1 функция имеет гладкий минимум, при x = 5 функция имеет гладкий максимум. На интервалах от -∞ до -3 и от -3 до +2 функция выпуклая (выпуклая вверх), на интервале от +2 до +7 функция вогнутая (выпуклая вниз). Функция имеет перегибы при x = 2 и при at x = 7.

Собственный пример авторов. Задание является нетрадиционным, творческим. Достоинства и недостатки такие же как в задании 5. Даже студенты, демонстрирующие честное поведение, обычно плохо справляются с этим заданием. Авторы рекомендуют предлагать такие задания только студентам физико-математических направлений подготовки.

Задание. 9. Найти односторонние производные функции при x = 0 (рис. 3). Функция задана на интервалах: при x < 0: y = x/2 + 1; при x > 0: y = (x – 2)2 – 3.

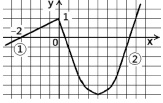
Рис. 3. Односторонние производные (задание 9)

Собственный пример авторов. Задание является нетрадиционным, творческим. Достоинства задания такие же, как и для задания 4. Для усложнения задания выражение для функции заменяется ее описанием. Авторы рекомендуют предлагать задание студентам всех направлений подготовки.

Тема «Интегральное исчисление функции одной переменной» («Интегралы»)

Задание 10. Найти неопределенный интеграл

.

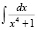Множество подобных интегралов было сконструировано преподавателями математических дисциплин в период, предшествующий массовому использованию интернет-сервисов. Авторы привели только самый простой по форме из них. Задание является традиционным, но творческим. Если студенту удается воспользоваться интернет-сервисами, то решение получается очень быстро. Честному студенту приходится тратить слишком много времени для решения. Возможные ошибки в громоздких вычислениях могут привести к неправильному ответу. Именно интегрированию посвящены основные дискуссии математиков на форумах, ориентированных на противодействие академической нечестности, там же приведены примеры интегралов, с которыми интернет-сервисы справляются плохо. Авторы не рекомендуют предлагать такие задания студентам.

Задание 11. Найти неопределенный интеграл

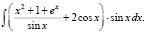
Задание является нетрадиционным, творческим. Основная идея – применение тождественных преобразований, затрудняющих непосредственное применение интернет-сервисов. Авторы рекомендуют предлагать задание студентам всех направлений подготовки только в случае гарантии честного выполнения.

Задание 12. Найти производную от определенного интеграла с переменными пределами.

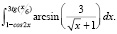
Задание является нетрадиционным, творческим. Авторы рекомендуют предлагать задание студентам всех направлений подготовки только в случае гарантии честного выполнения.

Задание 13. Найти площадь фигуры (рис. 4).

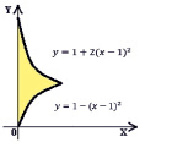
Рис. 4. Площадь плоской фигуры (задание 13)

Задание является традиционным, но творческим. Достоинства задания такие же, как и для задания 4. Для усложнения задания авторы предлагают заменить выражения для функций их словесными описаниями. Авторы рекомендуют предлагать задание студентам всех направлений подготовки.

Тема «Дифференциальное исчисление функции нескольких переменных»

Задание 14. Найти предел выражения

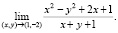
Источник – [13]. Задание является нетрадиционным, творческим. Как средство противодействия списыванию авторы оценивают его в 5 баллов из 5 возможных. Авторы рекомендуют предлагать такие задания преимущественно студентам физико-математических направлений подготовки только в случае гарантии честного выполнения.

Задание 15. Сконструировать формулы для производных сложной функции

.

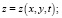
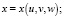
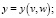
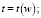
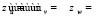Одно из достоинств задания – возможность быстрого решения честными студентами. Авторы рекомендуют предлагать задание студентам всех направлений подготовки.

Результаты исследования и их обсуждение

Авторы привели примеры творческих нетрадиционных заданий, которые позволяют преподавателям предотвращать проявления академической нечестности студентов на контрольных мероприятиях. Очевидно, что основные приемы, используемые математиками при составлении творческих заданий – использование нетрадиционных формулировок или условий поиска, использование графических образов, предложение сконструировать задание или математический объект. К нетворческим способам предотвращения списывания можно отнести использование громоздких заданий, заданий повышенной трудности либо заданий, требующих длительного времени для выполнения.

Авторы провели опрос 12 коллег – преподавателей математики Санкт-Петербургского политехнического университета Петра Великого, ориентированных на подготовку студентов по различным группам направлений – инженерным, исследовательским (физико-математическим) и экономическим (обозначены ЭN и занумерованы от 1 до 12). Всего на кафедре высшей математики этого вуза трудятся более 60 преподавателей. Каждое из 15 заданий просили оценить баллами от 1 до 5, выражающих в порядке возрастания эффективность противодействия списыванию (обозначены ЗN и занумерованы от 1 до 15). Результаты опроса приведены в табл. 1.

Очевидно, что оценки экспертов очень разнятся. Для того, чтобы выяснить согласованность мнений экспертов, вычисляем коэффициент конкордации Кендалла W:

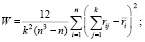
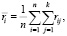
где n – число заданий, k – число экспертов, rij – оценка i-го задания j-м экспертом. Значение коэффициента конкордации W = 0,12 говорит о слабой согласованности мнений экспертов, что подтверждается проверкой гипотезы о согласованности оценок по критерию χ2 на уровне значимости 0,05 (т.е. с надежностью 95 %). Это значит, что средние значения оценок не дают надежной информации и в дальнейшем анализе использоваться не будут. Возможно, такие результаты получены вследствие относительно высокого возраста экспертов (от 43 до 75 лет), многие из которых имеют только самые общие представления о возможностях интернет-платформ для решения математических заданий. В то же время такой возрастной диапазон характерен для преподавателей математики российских вузов, что говорит об относительной объективности полученных данных.

Для подтверждения возможностей использования интернет-сервисов для решения заданий, авторы проводили их тестирование путем кратных решений, производя 3–4 повторения как одно за другим, так и в разные дни. Правильные ответы давались ситуативно, что связано со стохастическими принципами работы интернет-платформ. Также часто для получения правильного ответа требовалась коррекция текста. Ясно, что эти обстоятельства затрудняют попытки студентов прибегнуть к средствам академической нечестности, но при наличии коммуникаторов и людей-помощников эти обстоятельства преодолеваются нечестными студентами. Результаты этого исследования вместе с выводами приведены в табл. 2.

Таблица 2

Результаты анализа противодействию академической нечестности по группам заданий

Таким образом, выделились три группы заданий, которые в наибольшей степени, по мнению авторов, способствуют преодолению проявлений академической нечестности. Во-первых, использование задач с параметром, во-вторых, использование графических образов, в-третьих, предложение сконструировать формулу или математический объект.

Заключение

Авторы провели несколько исследований по выявлению математических заданий, использование которых на контрольных мероприятиях снижает, по мнению авторов, риски проявления академической нечестности студентов. В частности, авторы провели опрос преподавателей-экспертов. Выяснилось, что не все преподаватели представляют масштаб проявления академической нечестности (списывания) студентами вуза, а также возможности и арсенал вспомогательных средств. Кроме того, многие преподаватели уверены, что могут держать ситуацию под контролем, не позволяя студентам пользоваться коммуникаторами. Авторский практический опыт и изучение литературы показывает иллюзорность этих надежд ввиду мощности средств поддержки и изощренности технологий списывания отдельными студентами. Авторы предложили группы заданий, для решения которых использование интернет-сервисов затруднительно. Однако некоторые математики настороженно относятся к нетрадиционным заданиям, поскольку имеют свои устоявшиеся представления о способах формирования компетенций в области математики. Еще одним возражением является недоверие к графическим образам, которые, по мнению некоторых математиков, снижают меру абстрактности изложения и усвоения материала. Думается, что такой подход неприемлем в большинстве направлений инженерного образования, исключая, возможно, системотехнику и некоторые информационные технологии. Наконец, многие задания на конструирование отвергаются математиками как слишком простые, поскольку «там нечего решать», что, очевидно, является заблуждением относительно природы математики.

Использование предлагаемых заданий на контрольных мероприятиях должно, по мнению авторов, сопровождаться организационными мерами. А именно, во-первых, ограничением числа студентов, одновременно выполняющих задания, во-вторых, жестким ограничением времени выполнения заданий, в-третьих, полной диверсификацией банка заданий с целью исключения повторяющихся вариантов [14]. Несколько иной подход применяется авторами для предотвращения списывания при освоении студентами теории вероятностей [15]. Эти меры в совокупности с использованием нетрадиционных творческих заданий должны привести если не к исключению, но к снижению проявлений академической нечестности.