Обучение персонала можно представить как управляемый динамический процесс, направленный на достижение цели обучения всеми обучающимися (максимальное приближение к цели обучения), опираясь на текущий уровень знаний обучающегося, уровень его навыков и умений. Управление процессом обучения состоит из планирования процесса обучения, применение обучающих воздействий на каждом этапе обучения и контроль уровня обученности [1].
Целесообразно отметить, что процесс обучения с использованием учебно-тренировочных средств разделен на обособленную практическую и теоретическую части и обладает рядом особенностей [2]. Важной особенностью теоретической части является разделение программы обучения на обособленные части обучающего материала с фиксированным временем их изучения. Части обучающего материала состоят из основного материала, дополнительного и тестовой части. Переход от одной части к следующей определяется необходимостью выполнения теста.
Цель исследования – предложить комплекс математических моделей теоретического и практического обучения, которые позволят прогнозировать оптимальный план обучения эксплуатирующего персонала по критерию максимума вероятности выполнения задачи.
Материалы и методы исследования
При проведении исследования разработана модель процесса теоретического обучения в системе MathLab на основе накопленных данных о функционировании учебно-тренировочных средств. Проведено моделирование процесса практического обучения в системе MathCad с использованием выходных данных моделирования теоретического обучения. На основе выходных данных результатов моделирования теоретического и практического обучения проведено имитационное моделирование выполнения технологических операций с учетом закономерностей практического и теоретического обучения. В результате методом регрессионного анализа была определена целевая функция. Полученные при расчетах данные использованы для уточнения плана обучения. Под уровнем обученности в статье понимается значение уровня знаний (продолжительность изучения теоретического материала, продолжительность выполнения операций по идентификации неисправности, продолжительность выполнения операций по поиску причин неисправности, продолжительность выполнения операций по восстановлению работоспособного состояния оборудования).
Результаты исследования и их обсуждение
Подход к моделированию теоретического обучения
Обращая внимание на описанные выше особенности теоретической части обучения с использованием учебно-тренировочных средств, целесообразно описать процесс обучения с использованием конечной цепи Маркова с дискретным временем (рис. 1) [3]. Узел графа задет одну из составных частей процесса обучения (изучение основной части курса, тестирование, изучение дополнительной части курса и т.д.). С помощью дуг графа между узлами отображаются логические связи блоков с указанием вероятности перехода между блоками. Значение вероятности переходов от одного блока к другому зависит от индивидуальных способностей обучающегося, их возможно определить с использованием статистических методов и апостериорно корректировать.
Опираясь на основные положения теории цепей Маркова, возможно рассмотреть процесс обучения как динамическую систему, которая находится в одном из состояний в конкретный момент времени [4].
На рисунке
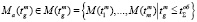– состояния, соответствующие этапам изучения теоретического материала.
На основе накопленных данных о функционировании учебно-тренировочных средств составляется матрица переходных вероятностей [5] (1), характеризующая начальный уровень теоретических знаний обучающегося.
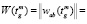
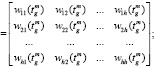(1)
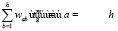
где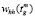 
– вероятность перехода между этапами изучения теоретического материала.
Получив из опытных данных фундаментальную матрицу Маркова (2), становится возможным вычисление средней продолжительности изучения теоретического материала (3), произвести оценку дисперсии продолжительности изучения теоретического материала (4) и среднеквадратичного отклонения продолжительности изучения теоретического материала (5) [6].
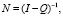(2)
где Q – матрица переходов между непоглощающими состояниями;
tтеор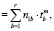 
(3)
где n1b – среднее количество попаданий в состояние,
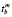– продолжительность нахождения в состоянии;
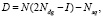(4)
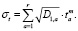(5)
Оставшееся для обучения время распределяется на совершенствование практических навыков идентификации, поиска причин и восстановление работоспособного состояния оборудования.
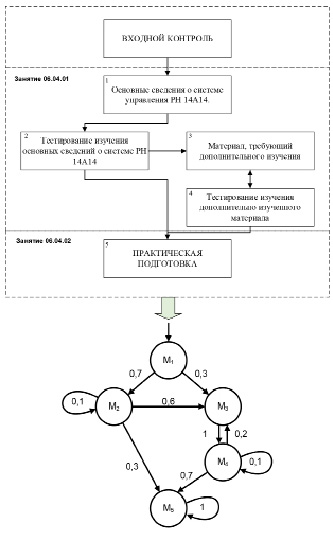
Рис. 1. Модель изучения теоретического материала
Подход к моделированию практического обучения
Анализ всевозможных математических моделей формирования практических навыков позволил установить, что наиболее подходящими моделями для практического обучения эксплуатирующего персонала являются:
– экспоненциальная модель для обучения идентификации (рис. 2);
– логистическая модель для обучения поиску причин (рис. 3);
– модель подкрепления для обучения восстановлению работоспособного состояния оборудования (рис. 4).
|
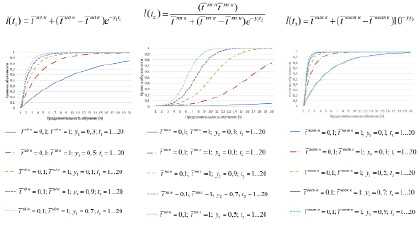
Рис. 2. Экспоненциальная модель |
Рис. 3. Логистическая модель Р. Буша |
Рис. 4. Модель подкрепления К. Халла |
Экспоненциальная модель [7].
Если предположить, что скорость изменения уровня обученности пропорциональна величине текущего уровня обученности, учитывая независимость коэффициента пропорциональности от времени.
Представим:
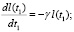(6)
где l(t1) – уровень обученности идентификации.
Решение данного дифференциального уравнения – экспонента представленная выражением
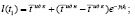(7)
В большинстве математических моделей изменения уровня обученности предполагается, что изменение уровня обученности за единицу времени пропорционально его текущему значению. Если задать коэффициент пропорциональности, то представленное допущение является следствием экспоненциального вида кривой изменения уровня обученности, при этом увеличение скорости изменения уровня обученности сопровождается необходимостью увеличения значения коэффициента рассогласования γ, который определяется различными моделями, как величина знаний, изученных обучающимся за единицу времени.
Модель Р. Буша [7].
Данная модель предполагает изменение уровня обученности на каждом из шагов пропорционально текущему уровню обученности и разности между некими текущим уровнем обученности и конечным. Изменение уровня обученности можно представить в виде дифференциального уравнения Бернулли:
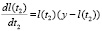, (8)
где y – константа, определяющая скорость изменения уровня обученности,
l(t2) – уровень обученности поиску причин.
Взяв за начальную точку t пп н, решением уравнения будет логистическая кривая:
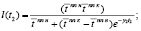(9)
«Тормозящий довесок» позволяет получить логистическую, а не экспоненциальную кривую за счет появления точки перегиба в отличие от рассматриваемой выше модели. Скорость изменения уровня обученности зависит от величины конечного уровня обученности и коэффициента пропорциональности между скоростью изменения уровня обученности и текущим значением обученности, что отличает модель от предыдущей (рис. 3).
Модель К. Халла [7].
Закономерность, по которой формируется навык, основывается на том, что, если внешние условия и цели обучения не изменяются, а подкрепления следуют равномерно, то уровень обученности l(t3) возрастает вместе с возрастанием числа повторений, что представлено равенством
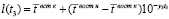, (10)
где l(t3) – уровень обученности восстановлению работоспособного состояния оборудования.
Применение комплекса моделей позволяет определить зависимость уровня практической обученности эксплуатирующего персонала, выраженного временем идентификации неисправности, поиска причин ее возникновения и восстановления работоспособного состояния оборудования от времени отведенного на процесс практического обучения в целом и на изучение соответствующих практических навыков в частности.
Заключение
Использование представленных в статье математических моделей обучения в комплексе позволяет провести имитационное моделирование выполнения технологических операций с учетом закономерностей практического и теоретического обучения (рис. 5).
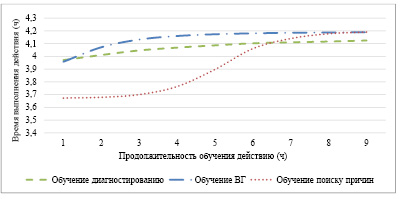
Рис. 5. Закономерности практического обучения
На основе полученных экспериментальных данных методом регрессионного анализа можно определить целевую функцию
t су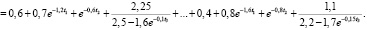 
где t су – продолжительность выполнения задачи, и прогнозировать оптимальный план обучения эксплуатирующего персонала по критерию максимума вероятности выполнения задачи методом динамического программирования (таблица).
Результаты применения моделей
|
|
tтеор |
|
|
|
Рвз |
|
|
Существующий план |
18 |
9 |
3 |
3 |
3 |
0,96 |
|
С использованием моделей (без изменения |
18 |
7 |
4 |
5 |
2 |
0,98 |
|
С использованием моделей (с изменением |
24 |
7 |
6 |
8 |
3 |
0,995 |
)
)Полученные при расчетах данные целесообразно использовать с целью уточнения плана обучения, что дает возможность создавать адаптированные по уровню знаний учебные курсы, проводить динамическую корректировку и анализ процесса изучения учебного материала, создавать прогноз времени обучения персонала, опираясь на его уровень обученности.
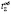
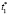
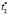
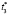
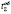