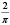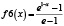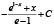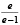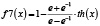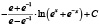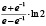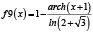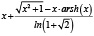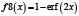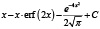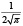Контроль технологических процессов проводится с целью обеспечения качества и безопасности выполнения работ путем своевременного обнаружения несоответствий и нарушений, которые могут повлечь за собой риск возникновения техногенной аварии, несчастного случая или остановки производства с причинением экологического и социально-экономического ущерба. При этом накопленные статистические данные наблюдений служат основой для апостериорной оценки профессионального риска, предусматривающей применение некоторого математического аппарата, в частности функций оценки риска.
Научно-методические основы оценки профессиональных рисков изложены в многочисленных работах, в том числе вопросы системного анализа и менеджмента техногенного риска [1], методик расчета риска [2], построения систем управления промышленной безопасностью [3], применение интеллектуальных систем поддержки принятия решений [4] и риск-ориентированного прогнозирования и предупреждения аварий [5], влияние условий труда на профессиональный риск [6], совершенствование условий безопасности и охраны труда на производственных объектах [7], оценки эффективности методов снижения экологического риска [8], принципы управления риском [9], критерии приемлемого риска [10], а также проблемы внедрения системы оценки и управления профессиональными рисками [11].
Кроме того, вопросы оценки и управления рисками регламентируются с нормативно-правовой стороны. Так, приказом Ростехнадзора [12] утверждено руководство по безопасности, устанавливающее методику проведения анализа опасностей и оценки риска аварий на опасных производственных объектах. А в стандарте системы менеджмента риска предлагается ряд других методик оценки риска [13]. В частности, для ранжирования и сопоставления рисков предложены несколько различных инструментов: индексы риска, матрицы вероятности/последствий, S – кривые и др.
Таким образом, состояние проблемы оценки профессиональных рисков находится в стадии совершенствования научно-методического и теоретико-практического инструментария, что определяет актуальность данной темы.
Постановка задачи исследования
Пусть в какой-либо системе требуется контролировать N параметров на соответствие установленным нормам или допустимым значениям. Тогда M – некоторое число параметров M⊂N, для которых выявлены несоответствия по результатам наблюдений за системой. Требуется дать количественную и качественную оценку результатов контроля. На основе вероятностного подхода можно определить первичную количественную характеристику риска, как относительную частоту несоответствий x в виде отношения
X = M / N, (1)
Определим функцию риска R(x) как непрерывную возрастающую функцию, определенную на интервале x ∈ [0,1], принимающую значения R(x) ∈ [0,1], выраженные в относительных единицах. Тогда функция f(x) = 1 – R(x) является противоположной по смыслу характеристикой уровня безопасности, надежности, качества и др. Таким образом, необходимо найти аналитическую функцию f(x), взаимосвязанную с функцией риска, как мерой несоответствий, и определить критерии качественного анализа значений такой функции для последующего принятия решений относительно текущего состояния контролируемой системы. Например, можно задать сегментацию функции оценки на четыре качественных уровня: L1 хороший, L2 удовлетворительный, L3 плохой, L4 критический (неприемлемый). Однако допустима и бинарная сегментация, как и сегментация на три, пять и более уровней.
Математическая модель функции оценки
Для количественной оценки уровня соответствия контролируемых параметров возьмем следующую функцию (рис. 1, а)
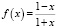 , (2)
, (2)
Её первообразная (рис. 1, б) имеет вид
F(x) = 2 ∙ ln(1 + x) – x + C, (3)
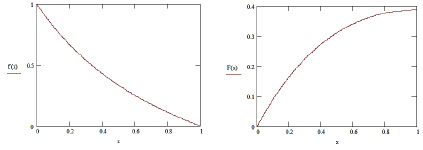
а) б)
Рис. 1. График функции оценки и ее первообразной
Выбор порогов сегментации функции оценки
В качестве критериев выбора порогов сегментации функции оценки можно использовать, например, задание уровней аргумента x или значений функции f(x), исходя из прикладной области, что требует дополнительного обоснования. Например, можно задать уровни согласно равномерному распределению. С другой стороны, можно определить пороги сегментации на основе соотношения площадей сегментов, ограниченных функцией оценки и осями координат. Способы задания отношений также могут определяться в контексте задачи. Например, можно использовать критерий равных площадей сегментов; критерий, базирующийся на принципе золотого сечения; прогрессивный критерий и др.
По критерию равных площадей площадь каждого из четырех сегментов одинакова Sk = 25%. По критерию золотого сечения вектор значений площадей сегментов составит
S = [φ4 φ3 φ3 φ2], (4)
где φ = 0,618034 – коэффициент пропорции, а φk – k-я степень числа φ.
Согласно прогрессивному критерию площади сегментов можно задать как соотношения членов геометрической прогрессии
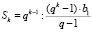 , (5)
, (5)
где b1 = q0 = 1 – первый член прогрессии; q – коэффициент пропорции.
Например, при q = 3 получим
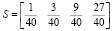 .
.
На рис. 2 показаны диаграммы соотношений площадей сегментов, найденным по разным площадным критериям.
Поскольку каждый сегмент представляет собой одну из четырех зон функции оценки f(x), то, задавая желаемые соотношения сегментов, можно управлять системой оценки исходя из текущих условий.
Площади зон сегментов функции оценки можно найти по формуле
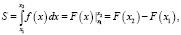 (6)
(6)
где F(x) – первообразная функции f(x).
Для определения значений порогов сегментов по заданным площадям сегментов функции оценки необходимо решить обратную задачу, то есть найти обратную функцию x = F –1(x). На практике аналитическое решение этой задачи может быть затруднительно. Поэтому воспользуемся численным методом решения эквивалентной задачи поиска корня уравнения (рис. 3), представляющего собой разностную функцию
f 2(x) – g2(x, F(x)) = 0, (7)
где f 2(x) = ln(1 + x)2; g2(x, F(x)) = x + F(x) –функции, составленные для функций (2) и (3).
Решение можно найти с помощью встроенной функции root в программе Mathcad. Результаты расчетов сведены в табл. 1 и показаны графически на рис. 4.
Сравнение полученных результатов показывает, что прогрессивный критерий является наиболее строгим из представленных, так как определяет более «жесткие» границы уровней сегментов. Оценка по данному критерию характеризует, что при контроле N = 100 параметров граничные значения количества несоответствий по сегментам составят: 1, 5, 15. Другими словами, уровень L1 обеспечивается, если зафиксировано менее одного несоответствия, уровень L2 – не более четырех несоответствий, уровень L4 – более четырнадцати несоответствий.
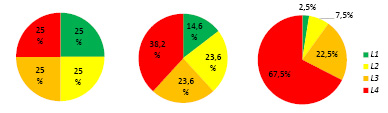
а) б) в)
Рис. 2. Сегментация функции оценки по критериям: а) равных площадей; б) золотого сечения; в) прогрессивный

Рис. 3. Поиск корня разностной функции
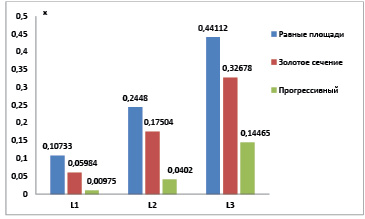
а)
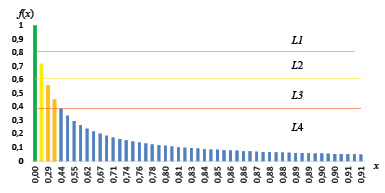
б)
Рис. 4. Результаты пороговой сегментации функции оценки: а) уровни сегментации функции оценки f(x) по различным критериям; б) пороговые значения сегментации функции оценки f(x) по критерию равных площадей
Таблица 1
Сегментация функции оценки по площадным критериям
|
Критерий |
Равные площади |
Золотое сечение |
Прогрессивный |
|||
|
Уровень |
x |
f(x) |
x |
f(x) |
x |
f(x) |
|
L1 |
0,10733 |
0,806 |
0,05984 |
0,8871 |
0,00975 |
0,9807 |
|
L2 |
0,24480 |
0,607 |
0,17504 |
0,7021 |
0,0402 |
0,9227 |
|
L3 |
0,44112 |
0,388 |
0,32678 |
0,5074 |
0,14465 |
0,7473 |
|
L4 |
> 0,44112 |
< 0,388 |
< 0,32678 |
< 0,5074 |
> 0,14465 |
< 0,7473 |
Таблица 2
Функции оценки в задаче анализа риска
|
№ |
f(x) |
F(x) |
C |
|
1 |
|
|
|
|
2 |
|
|
0 |
|
3 |
|
|
0 |
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
0 |
|
9 |
|
|
|
Результаты исследования и их обсуждение
Рассмотренная выше функция f(x) и методика оценки риска при контроле соответствия параметров системы (процесса) демонстрирует общий подход к решению задачи. В то же время можно определить класс функций оценки, соответствующих заданным требованиям, которые также можно использовать при анализе риска. Некоторые функции, принадлежащие данному классу, приведены в табл. 2 и на рис. 5.
Выбор конкретной функции оценки, критерия пороговой сегментации, количества сегментов определяется прикладными задачами.
Кроме того, если помимо фиксации числа несоответствий требуется учесть риск потенциальных последствий, можно ввести некоторую числовую шкалу значимости с заданными весовыми коэффициентами для оценки каждого зафиксированного несоответствия. В этом случае вместо формулы (1) можно использовать первичную оценку в виде скалярного суперкритерия
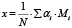 , (8)
, (8)
где αi – весовые коэффициенты значимости; Mi – число нарушений i-го типа, i ∈ [1, H].
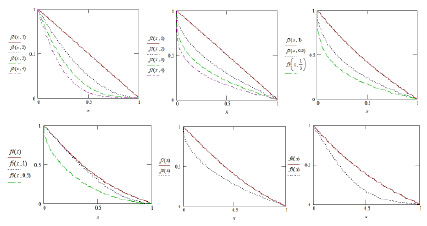 Рис. 5. Функции оценки
Рис. 5. Функции оценки
Количество типов нарушений H конечно и определяется возможным числом реальных или потенциальных последствий, качественно различающихся степенью социально-экономического и/или экологического ущерба.
Следует отметить, что предложенный подход к математическому моделированию риска вполне применим к задачам оценки уровня обученности производственного персонала, как и вообще уровня подготовки в системе обучения, на основе тестовой системы оценки знаний. Еще одной потенциальной прикладной областью применения рассмотренной методики является оценка степени износа в процессе диагностики состояния строительных конструкций.
Заключение
Резюмируя все вышесказанное, в работе предложена математическая модель функции оценки уровня безопасности, площадные критерии сегментации функции оценки на качественные уровни, алгоритм определения порогов сегментации. Представлены некоторые результаты моделирования и приводятся рекомендации практического применения модели.
Рассмотренная в данной работе методика оценки была апробирована в работе службы контроля безопасности выполнения работ на предприятии АО ВМЗ.





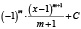
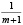
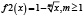
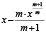
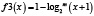
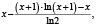 при m = 1
при m = 1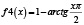
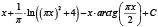
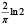
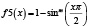
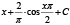 , при m = 1
, при m = 1