Современные магистральные трубопроводы транспорта природного газа являются инженерными системами, которые состоят из большого количества элементов, объединенных в объекты, выделим, что основным объектом магистрального газопровода, является газоперекачивающий агрегат компрессорной станции [1, 2].
Цель исследования: разработка методики диагностирования узла подшипника, который состоит из подшипника, вкладыша, масляного слоя ГТУ газоперекачивающего агрегата.
Материалы и методы исследования
Штатная система диагностики вибрации ТИК-РВМ, математическое моделирование.
К газоперекачивающим агрегатам (ГПА) предъявляют определенные требования:
− безотказность работы в течение всего периода эксплуатации;
− надежность работы ГПА при повышенных режимах эксплуатации магистрального газопровода.
Опыт длительной эксплуатации оборудования магистрального газопровода выявил наиболее слабые элементы, которые зачастую приводят к простою магистрального трубопровода, авариям и аварийным ситуациям. Выделим, что к таким элементам можно отнести газоперекачивающие агрегаты в силу специфики эксплуатации и сложности конструкции элементов газоперекачивающего агрегата, а также ухудшения физических параметров агрегата по причине износа деталей, материалов конструкции, усталостных напряжений, которые возникают в узлах, подверженных длительным нагрузкам.
Газоперекачивающий агрегат (ГПА) имеет множество уязвимых элементов, которые требуют своевременной диагностики и определения причины неисправности на ранних этапах развития дефектов [1]. К таким элементам можно отнести подшипниковый узел вала газотурбинной установки и нагнетателя, который подвержен длительным нагрузкам, и перегрузка в случай неправильного контакта масляного слоя между валом и подшипником (рис. 1).
Из рис. 1 видно, что масляный слой смазки выполняет несущую функцию, то есть принимает на себя нагрузку и создает в пятне контакта масляную подушку из смазки (так называемый гидродинамический клин), пятно контакта возникает при условиях соблюдения некоторых условий:
− трущиеся поверхности перемещаются относительно друг друга (в состоянии покоя масляного клина нет);
− между деталями находится жидкая среда или газовая (газодинамические подшипники);
− существует определенная форма трущихся элементов, в результате которого возникает зона разрежения для жидкости и газа, поэтому происходит затягивание в сужающую часть деталей трущихся поверхностей.
Диагностика подшипников и подшипниковых узлов газоперекачивающего агрегата выявила наиболее опасные повреждения, к ним можно отнести перекос осей втулки и шейки вала, биение шеек многоопорного вала и опор в картере.
Работоспособность подшипника подтверждается при выполнении следующих условий, к которым относится минимальный износ деталей, а также при выполнении условия устойчивости системы схватывания и механического разрушения как следствие деформации, стойкости к коррозионному износу материалов и усталостного сопротивления трещинам [2, 3].
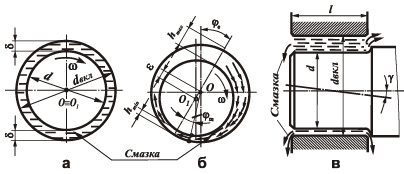
Рис. 1. Схема параметров подшипника: а – идеальное положение осей вкладыша и цапфы; б, в – реальное расположение вала во вкладыше подшипника [3]
Из рис. 1 видно, что масляный слой смазки выполняет несущую функцию, то есть принимает на себя нагрузку и создает в пятне контакта масляную подушку из смазки (так называемый гидродинамический клин), пятно контакта возникает при условиях соблюдения некоторых условий:
− трущиеся поверхности перемещаются относительно друг друга (в состоянии покоя масляного клина нет);
− между деталями находится жидкая среда или газовая (газодинамические подшипники);
− существует определенная форма трущихся элементов, в результате которого возникает зона разрежения для жидкости и газа, поэтому происходит затягивание в сужающую часть деталей трущихся поверхностей.
Диагностика подшипников и подшипниковых узлов газоперекачивающего агрегата выявила наиболее опасные повреждения, к ним можно отнести перекос осей втулки и шейки вала, биение шеек многоопорного вала и опор в картере.
Работоспособность подшипника подтверждается при выполнении следующих условий, к которым относится минимальный износ деталей, а также при выполнении условия устойчивости системы схватывания и механического разрушения как следствие деформации, стойкости к коррозионному износу материалов и усталостного сопротивления трещинам [2, 3].
Узел подшипника должен обеспечивать надежность при воздействии различных факторов. Современные материалы и компьютерное моделирование позволяют создавать сложные механические системы и узлы, но не существует идеальных систем, которые бы можно было бы адаптировать под любые условия эксплуатации. Поэтому на сегодня не существует подшипника, который бы удовлетворял всем требованиям, предъявляемым промышленностью, а в частности авиастроительной отраслью к конструированию газоперекачивающих агрегатов. Износ опор скольжения на работающем агрегате в условиях жидкостного трения является актуальной проблемой, на решение которой требуется направить весь научный потенциал, так как зачастую оно встречается очень часто на компрессорных станциях магистрального газопровода.
Изучением разрушения подшипников газоперекачивающих агрегатов занимается такая наука, как трибология, которая выдвигает современные гипотезы и математические модели, отражающие физику трения сопрягающихся деталей вала и подшипника.
При анализе установлены неисправности подшипников элементов ГТУ, нагнетателя по косвенным параметрам, авторами предложена упрощенная математическая модель диагностики данного узла. Данная модель представляет собой колебательную систему, состоящую из трех последовательных связанных гармонических осцилляторов, один из которых жестко закреплен. Данная модель представляет идеальную механическую конструкцию, позволяющую выявить закономерности и связи между собственными частотами при вибрациях ГПА и нагнетателя [3, 4].
Основа математической модели газоперекачивающего агрегата как колебательной системы
В основу математической модели положена упрощенная схема представления газоперекачивающего агрегата как единой колебательной системы, основанная на некоторых допущениях и обобщениях известных законов. Выделим, что моделирование является основным элементом научного познания, которое позволяет определить ряд параметров для оценки объекта исследования. В данной работе, мы исследуем газоперекачивающие агрегаты компрессорных станций магистрального газопровода и его элементы. Перед тем как приступить к моделированию, приведем небольшую классификацию, основанную на исследовании подобных систем, и виды неисправностей, которые в наибольшей степени могут быть обнаружены. К таким неисправностям можно отнести: дисбаланс деталей ротора, дефекты подшипника скольжения, дефекты в подшипниковых узлах, ослабления натяга на вкладышах подшипников, коробление корпусов при неправильном тепловом расширении, неисправности ротора и статора и т.д.
Для анализа газоперекачивающего агрегата как модели колебательной системы представим ее в виде схемы (рис. 2) [4, 5]:
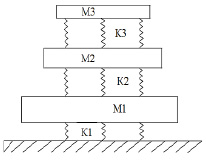
Рис. 2. Модель колебательной системы газоперекачивающего агрегата [1, 2]
1. Корпус (обозначим средний элемент системы).
2. Подшипниковый узел (подшипник, вкладыш, масляный слой) (обозначим верхний элемент).
3. Вал (обозначим нижний элемент).
Тогда M1, M2, M3 – массы элементов, K1, K2 и K3 – жесткости упругих соединений.
Выразим из уравнения Лагранжа идеальную механическую систему:
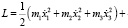
 . (1)
. (1)
В выражении (1)х1,2,3 – это смещение элементов от положений их равновесия; точкой обозначена 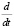 – производная по времени.
– производная по времени.
Тогда выразим уравнение движения механической системы в форме Лагранжа:
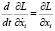 . (2)
. (2)
В выражении (2) i =1, 2, 3. Тогда получим систему уравнений
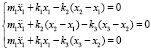 . (3)
. (3)
При подстановке в систему уравнений (3) вектора-столбца получим решения матрицы:
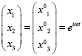 , (4)
, (4)
Которую в последующем используем для определения характеристических (собственных) частот [1, 3].
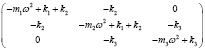 (5)
(5)
Анализируемые частоты находятся из характеристического (векторного) уравнения, которое выражает условие равенства нулю, определяется матрицей уравнения
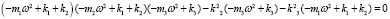 . (6)
. (6)
Из выражения (6) можно получить уравнение третьей степени, то есть кубическое уравнение относительно ω2, в связи с тем что матрица симметрична, ее собственные [3, 4] (частота в квадрате) значения вещественны, то для выполнения данного условия они должны быть еще и положительными.
Выражение (6) приведем к виду
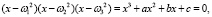 (7)
(7)
Произведем замену переменной х = ω2:
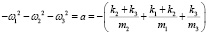 , (8)
, (8)
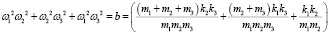 , (9)
, (9)
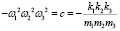 (10)
(10)
Тогда получим 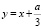 , выражение (7) принимает вид y3 + py + q = 0, где
, выражение (7) принимает вид y3 + py + q = 0, где 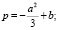
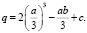 Тогда ввиду симметричности матрицы, выражение (5) и ее собственные члены, должны иметь вещественные значения.
Тогда ввиду симметричности матрицы, выражение (5) и ее собственные члены, должны иметь вещественные значения.
При выполнении условия, что 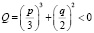 – то так называемый «неприводимый случай», в котором формулы Кардано для корней кубического уравнения могут иметь следующие (тригонометрические) представления [6, 7]:
– то так называемый «неприводимый случай», в котором формулы Кардано для корней кубического уравнения могут иметь следующие (тригонометрические) представления [6, 7]:
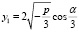 , (11)
, (11)
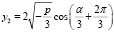 ;
;
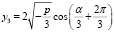 , (12)
, (12)
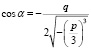 . (13)
. (13)
Из выражения при условиях, что p < 0 и Q < 0, которое равносильно тому, что |cos α| < 1, случай Q = 0, то есть cos α = 1 [8, 9]:
Тогда выражение (11), (13) примет вид
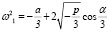 , (14)
, (14)
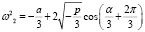 , (15)
, (15)
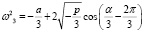 . (16)
. (16)
В выражениях (14), (15), (16)
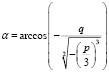 ,
,
который изменяется в интервале 0 < α < π, для общего сведения тригонометрическое представление корней имеет вид
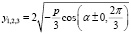 .
.
Это проверяется непосредственной подстановкой и использованием тожества
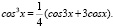
Получим:
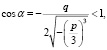
то есть 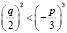 , при Q < 0.
, при Q < 0.
Случай же Q = 0, то есть cos α = 1, то α = 0 и 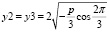 . Это кратность корней – вырождение.
. Это кратность корней – вырождение.
Проверка модели на адекватность
Для проверки результатов, полученных в данном исследовании, необходимо соблюдение условия, что произвольных m1,2,3 и k1,2,3 по формулам (1), (2) и (3) вычисляются частоты (в квадрате ω21,2,3) и они положительны. После этого они подставляются в выражение (6), где проверяется условие, при котором они приближенно равны (≈ 0).
Отметим, что коэффициенты k1, k2, k3, считаются неизвестными и характеризуют жесткость системы. Известными величинами является масса корпуса, движущегося подшипника и вала, частоты (ω1,2,3 = 2πγ1,2,3) измеряются вибрографом.
Из уравнений (1), (2) и (3) находятся неизвестные k1, k2, k3 каким-либо численным методом, например, встроенным в Excel или MathCad.
Методика диагностики заключается в том, чтобы следить за изменениями коэффициентов жесткости k1, k2, k3 путем сопоставлением их с обнаруживаемыми неисправностями, а также оценки значения коэффициентов, которые при расчетах могут сильно уменьшаться, что является косвенным показателем появления износа подшипника, трещин, осевого сдвига вала и дисбаланса ротора.
Для проверки полученных результатов необходимо провести проверку результатов. Далее проведем эксперимент на радиально-упорном подшипнике скольжения ГПА. И проанализируем рис. 3, который предоставила система ТИК-РВМ.
Система предназначена для постоянного мониторинга, отображения, контроля и хранения, а также анализа параметров вибраций ГПА и его механического состояния.
Установлено, что работоспособность узла подшипника сильно связана с правильной центровкой ротора, а также она подвержена влиянию тепловых перемещений фундаментных колонн под ГПА, тепловых перемещений корпуса турбины и нагнетателя под действием усилия со стороны патрубков.
Исследование газоперекачивающего агрегата компрессорной станции «Донская» проводилось в два этапа, на первом этапе анализ работы и установление стабильного режима и снятие показаний, на втором этапе калибровка приборов и диагностика, а также обработка полученных данных с помощью математической статистики. Выборка и анализ заведомо неправильных показаний (поверка).
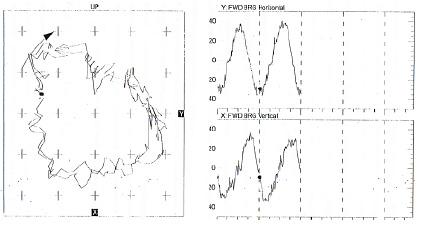
а б
Рис. 3. Вращение вала и радиально-упорного подшипника скольжения:
а – отклонения вала ГПА по осям (X и Y);
б – вертикальное и горизонтальное отклонение вала ГПА [1, 3]
Из рис. 3 мы видим, что вращение вала газоперекачивающего агрегата и подшипника скольжения. В левой части приводится траектория и направление оси вращения Y к оси X, в правой части рисунка разложено колебание по оси Х с вертикальной составляющей. Исследование проводилось на компрессорные станции «Донская». Из данного графика на рис. 3, мы можем получить все необходимые данные для нашей модели.
Расчетная часть
При разработке данной математической модели были учтены параметры конкретного газоперекачивающего агрегата, который эксплуатируется на компрессорной станции «Донская». Исследование данного агрегата проводилось при максимальных нагрузках с рабочим давлением 5,6 Мпа, температура природного газа на входе 27 °С.
Из рис. 3 получили следующие данные:
1. Условный период колебания масляного слоя –T = 10–3 c
2. Частота вращения масляного слоя – n – 3000 об/мин.
3. Угловая скорость вращения
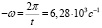 .
.
4. Разность перемещения l = 2,5 · 10–6 м.
Для наших расчетов условно возьмем следующие величины:
1. Масса вала центробежного компрессора m = 50 кг.
2. s = 0,5 · 10–2 м2 – площадь поперечного сечения.
3. Максимальное перемещение масляного слоя L = 8ΔL = 0,002 мм.
Выразим условную жесткость колебаний «k» между валом и масляным слоем из формулы 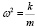 и получим
и получим
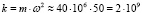 н/м.
н/м.
Отсюда можно найти давление, оказываемое масляным слоем на поверхность вала:
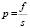 . (17)
. (17)
В выражении (17) f – это сила, с которой масляный слой давит на вал газоперекачивающего агрегата вместе контакта.
Из закона Гука выражение (17) известно, что f = kΔl, таким образом, мы окончательно получим
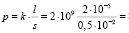
= 8 ∙ 106 Па (≈ 0,8 кгс/мм2)
Из литературного обзора установлено, что характеристики, полученные в результате исследования, совпадают с характеристиками материала, близкого к каучуку [7, 8]. В связи с этим в результате обсуждения авторы пришли к мнению, что для приближенного прогнозирования поведения масляного слоя в радиально-упорном подшипнике скольжения, необходимо на вибростенде провести испытания на каучуке с помощью создания вынужденных колебаний [9, 10] на вибростенде, а затем по параметрам жесткости установить зависимости, позволяющие дать характеристику поведению масляного слоя в подшипнике.
Заключение
Авторами предложена оригинальная математическая модель, может дать характеристику маслу и определить интервал времени для его замены. В созданной математической модели, которая прошла лабораторные испытания, применен новый подход к прогнозированию состояния подшипника вала ГПА. Полученные данные и виброграммы можно сравнить с реальными данными с учетом погрешности измерений, они позволят прогнозировать дефекты подшипника и вкладыша, а также их можно реализовать в алгоритм для диагностики данного узла газоперекачивающего агрегата. Предложенная авторами математическая модель может быть реализована в алгоритм на любом из известных языков программирования, это позволит собирать данные с разных газоперекачивающих агрегатов для определения неисправностей и выявления узлов, которые в наибольшей степени подверглись износу в процессе эксплуатации. Создание подобного приложения сильно облегчит работу специалистов, которые занимаются диагностированием газоперекачивающих агрегатов, и повысит уровень надежности оборудования и основных узлов агрегата. Также выделим, что приведенные математические выкладки легко алгоритмизируются и не требуют от языка программирования специальных математических функций, которые бы увеличили время вычисления и определения поврежденных узлов газоперекачивающего агрегата. Кроме этого, данная математическая модель может служить диагностической или мониторинговой системой предупреждения неисправностей узлов газоперекачивающего агрегата компрессорной станции магистрального газопровода.



