В настоящее время в задачах анализа текстов на естественном языке используются в основном нейросетевые модели и модели машинного обучения. Ключевым недостатком подобных моделей можно назвать проблему «чёрного ящика», при которой результаты работы модели сложно интерпретировать, а достоверность не является гарантированной в силу возможного переобучения полученной модели [1]. К тому же в большинстве своём такие модели требуют для своего обучения больших объёмов предварительно собранных данных [2–4]. В [5] приведено исследование способов использования энтропийных моделей в анализе текстовых данных, однако в [5] энтропийные модели используются только в качестве вспомогательного инструмента. Энтропийные модели эффективно используются в различных приложениях [6–10], поэтому представляется, что их можно успешно применить и в задаче анализа текстов на предмет возможного заимствования. В [11] была введена дифференциальная энтропия взаимосвязи между случайными векторами.
Целью статьи является исследование возможных путей использования модели энтропии взаимосвязи в анализе текстов на естественном языке, например при поиске схожих синтаксических конструкций либо заимствований фрагментов одного текста в другом.
Ключевым аспектом, потенциально позволяющим получить такие результаты, является свойство энтропии взаимосвязи возрастать в случае схожести двух случайных величин, что проистекает из того факта, что энтропия, по сути своей, является мерой хаоса. Таким образом, определяя энтропию взаимосвязи двух случайных величин, мы получим меру взаимного хаоса, или, если пойти от обратного, взаимной упорядоченности рассматриваемых случайных величин.
Однако для того, чтобы идея использования энтропии взаимосвязи для анализа связи текстов на естественном языке могла быть использована, требуется привести рассматриваемые тексты в вид, к которому метод расчёта энтропии взаимосвязи может быть применён, что фактически требует преобразования текста на естественном языке к виду численной случайной величины, или, другими словами, вектора случайных значений.
Таким образом, первая задача, которая должна быть решена – это преобразование текста на естественном языке в некий упорядоченный вектор случайных значений, который в дальнейшем будем называть отношением порядка. Существует множество способов преобразовать текст в вектор чисел, например: мешок слов, матрица TF-IDF, Word2Vec [12, 13]. В случае рассматриваемой задачи нами было решено разработать для апробации метода несколько простых отношений порядка, представляющих собой различные уровни обобщения текстовых данных.
Также для корректного преобразования текстовых данных требуется, чтобы для каждого из рассматриваемых текстов для кодирования одинаковых слов использовались одинаковые численные значения. Достичь этого позволяет простая идея создания общего словаря путём объединения рассматриваемых текстов в один и сопоставления каждому из представленных слов того или иного значения.
Так как проблема преобразования текстов на естественном языке к виду случайных величин была решена, нам удалось применить метод исследования взаимосвязи текстов на основе расчёта дифференциальной энтропии взаимосвязи между этими текстами. Однако модель дифференциальной энтропии взаимосвязи предполагает, что рассматриваемые случайные величины имеют одинаковое число элементов в каждом случайном векторе, другими словами, мы можем сравнивать только тексты или фрагменты текстов, одинаковой длины. Также, в зависимости от используемого отношения порядка, метод может быть эффективен на текстах различных размеров, это зависит как от разнообразия словаря, так и от обобщающей способности используемого отношения порядка.
Для проверки работоспособности предложенного метода и отношений порядка был разработан эксперимент, включающий в себя апробацию рассматриваемых метода и отношений порядка на фрагментах текстов различной длины. Также в рамках этого эксперимента был предложен алгоритм, потенциально позволяющий находить заимствованные фрагменты одного текста в другом. Главной идеей алгоритма является простой проход окном с шагом в одно слово, фрагментом из одного текста по другому тексту, при этом на каждом шаге вычисляется дифференциальная энтропия взаимосвязи.
Материалы и методы исследования
Математическая модель энтропии взаи- мосвязи.
Энтропия взаимосвязи двух случайных векторов X и Y определяется как [11]
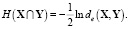(1)
В частности, для двух случайных величин X и Y, формула (1) принимает вид
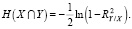(2)
Так как вид регрессионной зависимости в общем случае неизвестен, то согласно [9] вместо теоретического коэффициента детерминации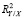 
можно воспользоваться эмпирическим коэффициентом детерминации
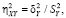
где
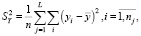(3)
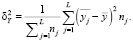(4)
В (3), (4) приняты следующие обозначения: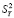 
– общая дисперсия переменной Y; L – число групп разбиения (X, Y); nj – размер j-й группы, 
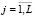; yj.i – элементы j-й группы; 
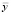– среднее значение всей переменной Y; 
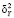– межгрупповая дисперсия переменной Y; 
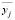– среднее значение переменной Y по j-й группе. В результате формула (2) принимает вид
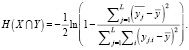(5)
В случае полного совпадения сравниваемых фрагментов текстов H(X∩Y) = +∞, поэтому для формулы (5) была выполнена регуляризация:
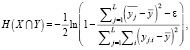(6)
где ε = 10-3 – параметр регуляризации.
Построение объединённого словаря.
Пусть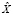 
и 
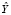– рассматриваемые тексты на естественном языке. Тогда 
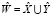– результат конкатенации рассматриваемых текстов 
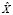и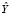 
. В таком случае словарём объединения текстов 
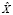и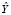 
будем считать множество V = {v1,v2,..,vn}, где vm – численное представление соответствующего уникального слова в словаре, полученное посредством преобразования исходного слова в соответствии с выбранным отношением порядка.
Построение отношений порядка.
Пусть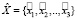 
– текст на естественном языке, где 
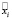– слово на i-й позиции в тексте 
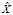, а Ord(a) – оператор преобразования слова a к выбранному отношению порядка. Тогда X = {x1,x2,..,xn}, где 
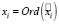– случайная величина, полученная посредством преобразования слов текста 
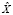в соответствии с выбранным отношением порядка.
Разработанные отношения порядка.
Для представления исследуемых текстов на естественном языке в виде векторов числовых значений были предложены следующие четыре отношения порядка:
1. Частотные отношения порядка имеют вид
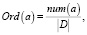(7)
где Ord(a) – оператор преобразования к отношению порядка, a – преобразуемое слово, num(a) – число вхождений слова a в словарь, |D| – длина рассматриваемого текста.
Данное отношение порядка представляет предположение о том, что слово может быть представлено как число его вхождений в рассматриваемый текст, нормированное длиной рассматриваемого текста. Предполагаемая обобщающая способность невысокая, особенно на словарях, построенных на основании текстов на специальном языке, особенно в случае их малой длины.
2. Лексикографические отношения порядка:
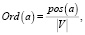(8)
где Ord(a) – оператор преобразования к отношению порядка, a – преобразуемое слово, pos(a) – позиция слова a в сортированном лексикографически списке уникальных слов рассматриваемого текста, |V| – размер словаря V.
Данное отношение порядка представляет предположение о том, что слово может быть представлено как его нормированное положение в сортированном словаре рассматриваемого текста. Предполагаемая обобщающая способность невысокая, особенно на словарях, построенных на основании текстов на специальном языке, особенно в случае их малой длины.
3. Случайные отношения порядка:
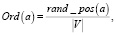(9)
где Ord(a) – оператор преобразования к отношению порядка, a – преобразуемое слово, rand_pos(a) – случайное значение от 0 до |V|, при этом каждое значение выдаётся единожды, таким образом обеспечивается уникальность кодирования каждого слова, |V| – размер словаря V.
Данное отношение порядка представляет предположение о том, что слово может быть представлено как его нормированное положение в словаре со случайным порядком рассматриваемого текста. Предполагаемая обобщающая способность невысокая, особенно на словарях, построенных на основании текстов на специальном языке, особенно в случае их малой длины. Данное отношение порядка разработано с целью проверки гипотезы о том, что энтропия взаимосвязи устойчива к конкретным значениям в случайных величинах и опирается только на взаимную упорядоченность рассматриваемых случайных величин.
4. Морфемные отношения порядка:
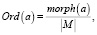(10)
где Ord(a) – оператор преобразования к отношению порядка, a – преобразуемое слово, morph(a) – номер морфемы, соответствующей слову a в списке морфем рассматриваемого языка, |M| – число морфем в рассматриваемом языке.
Данное отношение порядка разработано с целью поиска схожих синтаксических конструкций в рассматриваемых текстах, опираясь на предположении о возможной замене отдельных слов исходного заимствованного фрагмента текста словами-синонимами. Также, возможно, позволит в определённой степени определять автора текста, основываясь на характерных синтаксических конструкциях. Предполагаемая способность к обобщению довольно высокая.
Проблема текстов разной длины.
Так как метод расчёта энтропии взаимосвязи предполагает, что рассматриваемые случайные величины должны быть одинаковой длины, принято решение об использовании метода прохода фрагментом одного текста по другому тексту окном с шагом 1.
Общий алгоритм поиска возможных заимствований приведен на рис. 1.
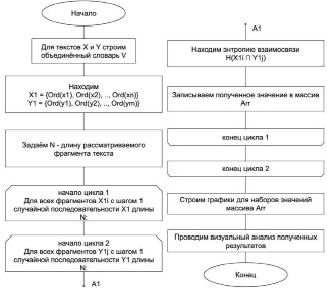
Рис. 1. Блок-схема общего алгоритма поиска возможных заимствований
Исходные данные
В качестве исходных данных для экспериментов использовались фрагменты различных художественных и научных текстов на естественном языке. Представленные в данной статье результаты экспериментов получены при использовании в качестве исходных данных фрагмента текста Михаила Булгакова «Белая гвардия» [14].
Результаты исследования и их обсуждение
Эксперимент проводится с целью показать, что разработанный алгоритм поиска возможных заимствований применим на практике и даёт прогнозируемый, легко интерпретируемый и достоверный результат. Эксперимент состоит из следующих этапов:
1) выбирается один фрагмент рассматриваемого текста;
2) в этом фрагменте текста выбирается фрагмент длины N, который будет считаться заимствованным;
3) для исходного фрагмента текста и выбранного заимствованного фрагмента выполняются шаги из алгоритма поиска возможных заимствований;
4) для полученных результатов строятся графики и проводится анализ;
Энтропия взаимосвязи характеризует степень взаимосвязи между двумя случайными последовательностями. В случае рассматриваемого эксперимента максимум значения энтропии взаимосвязи должен означать место заимствования фрагмента текста. Ожидается резкий скачок значения энтропии взаимосвязи в точке заимствования фрагмента текста. Также возможны другие скачки значения энтропии взаимосвязи в местах, имеющих высокую взаимосвязь с заимствованным фрагментом текста.
Рассмотрим результаты эксперимента.
На представленных ниже рис. 2–5 для каждого из экспериментов на оси абсцисс находятся номера слов в тексте, являющиеся стартовой точкой для итерации эксперимента, на оси ординат – значение энтропии взаимосвязи между заимствованным фрагментом текста и фрагментом текста, начинающимся с соответствующей стартовой точки. На рисунках под буквами «а», «б», «в», «г» располагаются графики для частотного, лексикографического, случайного и морфемного отношений порядка соответственно. Для большей наглядности показано окно по горизонтальной оси с 950 по 1050 стартовую точку, так как этот отрезок является ближайшей окрестностью места заимствования фрагмента текста, которое производилось всегда начиная со стартовой точки 1000, при этом длина заимствованного фрагмента варьировалась.
1. Длина заимствованного фрагмента текста 100 слов.
Для всех отношений порядка характерен скачок значения энтропии взаимосвязи в месте заимствования фрагмента текста. Различия между пиковыми значениями энтропии взаимосвязи на разных графиках можно объяснить вычислительной погрешностью. Также стоит отметить, что графики на рис. 2 практически идентичны, несмотря на то, что каждый соответствует своему отношению порядка.
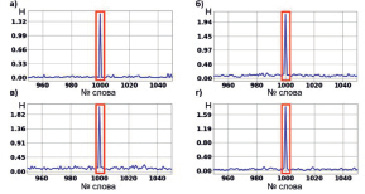
Рис. 2. Энтропия взаимосвязи для эксперимента с фрагментом текста длиной 100 слов для каждого из рассматриваемых отношений порядка
2. Длина заимствованного фрагмента текста 50 слов.
Для всех отношений порядка характерен скачок значения энтропии взаимосвязи в месте заимствования фрагмента текста. Различия между пиковыми значениями энтропии взаимосвязи на разных графиках рис. 3 можно объяснить вычислительной погрешностью. Практически полное отсутствие различий между графиками для разных отношений порядка продолжает сохраняться.
3. Длина заимствованного фрагмента текста 25 слов.
Для всех отношений порядка характерен скачок значения энтропии взаимосвязи в месте заимствования фрагмента текста. Различия между пиковыми значениями энтропии взаимосвязи на разных графиках можно объяснить вычислительной погрешностью. Также на графиках рис. 4 видно появление дополнительных скачков значения энтропии взаимосвязи, что говорит о том, что модель начинает обнаруживать фрагменты текста, имеющие слабую взаимосвязь с заимствованным фрагментом. В остальном, больших различий между графиками так и не появилось.
4. Фрагмент текста длиной 10 слов, начиная с 1000 слова.
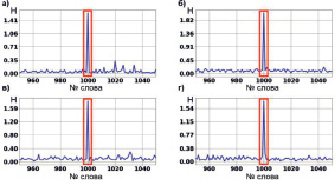
Рис. 3. Энтропия взаимосвязи для эксперимента с фрагментом текста длиной 50 слов для каждого из рассматриваемых отношений порядка
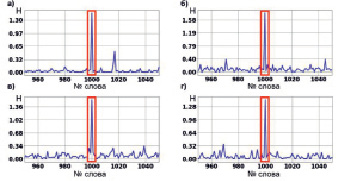
Рис. 4. Энтропия взаимосвязи для эксперимента с фрагментом текста длиной 25 слов для каждого из рассматриваемых отношений порядка
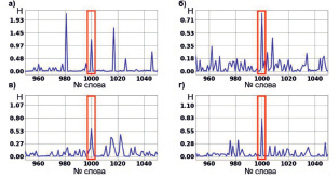
Рис. 5. Энтропия взаимосвязи для эксперимента с фрагментом текста длиной 10 слов для каждого из рассматриваемых отношений порядка
На рис. 5 на каждом из графиков появляются скачки значения энтропии взаимосвязи, сравнимые с пиком в месте заимствования фрагмента текста, причём некоторые по значению превосходят этот пик, однако это можно объяснить погрешностью вычислений. Исходя из появления дополнительных скачков значения энтропии взаимосвязи, можно утверждать, что для фрагментов текста длиной около 10 слов разработанный метод имеет высокую обобщающую способность, позволяя находить большое число схожих фрагментов текста. Такое поведение модель показывает на всех рассмотренных отношениях порядка, кроме морфемного, где значения дополнительных пиков значительно отличаются от значения в месте заимствования фрагмента текста. Также на фрагментах текста длиной около 10 слов появляются существенные различия между графиками для разных отношений порядка.
Повторяемость эксперимента
С целью проверки достоверности результатов эксперимента, а также повторяемости работы алгоритма, эксперимент был повторно произведён на ряде других художественных произведений отечественных авторов. Результат проведённых экспериментов позволяет утверждать о повторяемости работы алгоритма, приведённого в данной статье.
Заключение
Предложенный в данной статье метод позволяет получить легко интерпретируемый результат, причём для его работы не требуются большие наборы исходных данных. Этого удаётся достигнуть посредством использования дифференциальной энтропии взаимосвязи, физический смысл которой крайне прост для понимания, а также в силу кодирования исходных данных при помощи простых для интерпретации отношений порядка. К минусам предложенного метода можно отнести высокие требования к вычислительным ресурсам и большие затраты времени на анализ.
Также, исходя из рассмотренных примеров проведённого эксперимента, можно сделать вывод о том, что выбранное кодирование практически не влияет на итоговый результат, за исключением фрагментов малой (около 10 слов) длины, где использование различных отношений порядка начинает приводить к появлению существенных отличий в значении энтропии взаимосвязи в соответствующих точках. Таким образом, на фрагментах средней и большой длины все рассмотренные отношения порядка дают практически идентичный результат, тогда как сравнение предложенного алгоритма с использующимися в настоящее время методами представляется довольно сложным, в силу того что разработанный алгоритм не предполагает наличие стадии обучения модели, что делает его в корне отличным от использующихся аналогов. Преимуществом алгоритма является лучшая интерпретируемость результатов анализа из-за использования формальной модели, не требующей обучения.
Результаты анализа проведённого эксперимента позволяют говорить о возможности эффективного использования энтропийных моделей для решения задач анализа текстов на естественном языке.
Работа выполнена при финансовой поддержке гранта РФФИ, проект № 20-51-00001.