Нейронные сети (НС) получают все большее применение в различных системах управления, сбора и обработки информации, принятия решений и др. Характерные области применения, реализации и функции, выполняемые НС: 1) оптимальный фильтр объекта управления; 2) регулятор; 3) модель объекта управления; 4) комбинированный регулятор – регулятор типа П, ПИ, ПИД в сочетании с регулятором с нечеткой логикой; 5) регуляторы другого типа; 6) распознаватель или классификатор образов; 7) модуль принятия решений. Преимущества контроллеров, построенных с применением НС, в таких системах определяются следующими факторами: 1) быстродействие; 2) универсальность; 3) обучаемость; 4) отказоустойчивость; 5) простота применения.
В контексте нейронной сети обучение рассматривается как процесс настройки весов связей между нейронами из условия минимизации требуемого параметра оптимизируемой системы или процесса управления. По закону изменения параметров сети методы обучения делятся на детерминированные методы и стохастические. Первые основаны на коррекции параметров сети по текущим характеристикам величин входных, фактических и желаемых выходных сигналов. В классе детерминированных методов выделяются следующие основные подклассы в части алгоритмов обучения [1–3]: 1) по правилу Хэбба и Хопфилда; 2) методом выстраивания показателей; 3) коррекции по ошибке (желаемый вход-выход для всех ситуаций) и др.
Цель исследования: провести анализ алгоритмов настройки нейронной сети на основе градиентных методов первого порядка. При этом оценить влияние различных функций активации на показатели процесса настройки. Процесс настройки анализируется для типового входного воздействия систем автоматического управления – гармоническом входном сигнале.
Материалы и методы исследования
Методы обучения нейронных сетей. Рассмотрим аналитическое представление градиентных алгоритмов первого порядка, подлежащих анализу эффективности процесса обучения [4–6]. Эти алгоритмы основаны на коррекции параметров нейронной сети в функции градиента. В эту группу алгоритмов входят: метод градиентного спуска, метод моментов с регуляризацией, метод quickProp, метод rProp, метод сопряженных градиентов, метод NAG, метод AdaGrad (AdaptiveGradient), метод AdaDelta, метод Adam.
Градиентный метод первого порядка. Общий алгоритм обучения, реализуемый градиентными метода первого порядка, предусматривает следующую последовательность процедур.
1. Инициализация весов нейронной сети W.
2. Вычисление текущей ошибки E(h(X, W), C)).
3. Если значение ошибки находится в допустимом диапазоне, то коррекция параметров сети не требуется – конец работы.
4. Вычисление значения градиента функции потери: 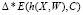 , здесь и далее Δ* – градиент функции.
, здесь и далее Δ* – градиент функции.
5. Вычисление изменения параметров: 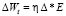 .
.
7. Коррекция параметров сети Wt = = Wt–1 – ΔWt. Здесь и далее индекс «t» обозначает текущую итерацию, индекс «t-1» – предыдущую.
8. Переход на п. 2.
Параметр η (скорость обучения) определяет величину шага процесса оптимизации, значение данного параметра находится в диапазоне 0 < η < 1.
Согласно п. 4 определяем градиент функции потери по выражению
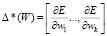 ,
,
где k – общее количество весов сети.
Составляющие определяются
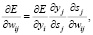
где E – функция потери; wij – вес связи нейронов i и j; yj – выход нейрона j; sj – состояние нейрона j.
Ошибки определены только для нейронов выходного слоя. Ошибки в скрытых и выходном слое соответственно определяются:
- для выходного слоя 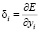 ;
;
- для скрытого слоя 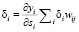 .
.
Совокупность процедур определения градиента функции потерь методом обратного распространения ошибки:
1) вычисление состояния нейронов s всех слоев сети – прямой проход;
2) определение 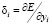 для выходного слоя;
для выходного слоя;
3) вычисление для скрытых слоев δi в обратном порядке – обратный проход;
4) определение 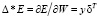 для каждого слоя и вычисление.
для каждого слоя и вычисление.
Метод обучения на основе обратного распространения ошибки (Backpropagation) предусматривает базовую последовательность процедур с учетом алгоритма обратного распространения ошибки.
На основе базового метода разработаны его модификации, состоящие в коррекции поправок при вычислении поправки ΔWt. Ниже приведем только результирующие выражения [4].
Метод моментов с регуляризацией. Классический метод градиентного спуска может «застревать» в локальных минимумах функции потери E, для предотвращения данных событий, широкое распространение получила модификация данного метода с использованием стратегии mini-batch и «моментов». Формально это описывается добавлением слагаемого к изменению весов:
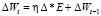 ,
,
где μ – коэффициент момента.
Одна из модификаций метода состоит в применении регуляризации, которая для борьбы с переобучением налагает штраф на чрезмерный рост значений весов:
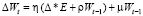 ,
,
где ρ – коэффициент регуляризации.
Для увеличения скорости сходимости процесса обучения можно ввести адаптивный коэффициент обучения, изменяемый на каждой итерации t в зависимости от изменения ошибки E.
Метод quick Prop. Отличие данного метода от рассмотренного выше состоит в том, что параметр момента μ и коэффициент скорости обучения η задаются индивидуально для каждого параметра. Изменение параметров описывается соотношением
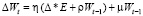 .
.
Метод r Prop. Является модификацией рассмотренного выше quickProp, в которой применяется стратегия full-batch. При этом параметр скорости обучения η рассчитывается для каждого веса индивидуально. Изменение параметров весов определяется соотношением
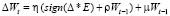 .
.
Метод сопряженных градиентов. Основан на специальном выборе направления изменения параметров, являющимся ортогональным к предыдущим направлениям. Изменение весов в этом случае имеет вид
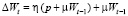 .
.
Коэффициент скорости обучения η, направление изменения параметров р, коэффициент сопряжения β вычисляются на каждом шаге путем решения задачи оптимизации:
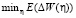 .
.
Для компенсации накапливающейся погрешности предусмотрен сброс сопряженного направления, т.е. β = 0, 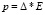 через каждые n циклов, число которых выбирается в зависимости от количества параметров сети.
через каждые n циклов, число которых выбирается в зависимости от количества параметров сети.
Метод Nesterov’s Accelerated Gradient (NAG). Здесь градиент вычисляется относительно сдвинутых на значение момента весов
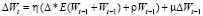 .
.
Метод Adaptive Gradient (AdaGrad). В группе адаптивных оптимизационных алгоритмов (Adagrad, RMSProp, Adadelta, Adam, NAdam) реализована динамическая модификация скорости обучения. Обновления производятся для значений признаков, представленных в меньшинстве, а более слабые обновления – для часто встречаемых значений. Этот принцип реализуется за счет того, что скорость обучения здесь фактически вычисляется отдельно для каждого из параметров на каждом шаге/такте обучения. При этом учитывается история значений градиентов gt. Выражение для изменения весов имеет вид
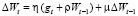 .
.
Метод AdaDelta. Является модификацией метода Adagrad и также учитывает историю значений градиента и историю изменения весов, однако при этом вместо полной суммы обновлений используется усреднённый по истории квадрат градиента (как экспоненциально затухающее бегущее среднее). Изменение весов аналогично.
Метод Adam (adaptive moment stimation). Сочетает в себе и идею накопления движения, и идею более слабого обновления весов для типичных признаков. Здесь используются «свои» аналитические выражения для коррекции градиента ошибки. Изменение весов аналогично.
Метод N Adam. Данный метод представляет собой модификацию метода Adam. Предусматривает коррекцию параметра учета истории значений градиентов gt.
Функции активации. Выходной сигнал нейрона определяется непосредственно видом функции активации. Наибольшее распространение получила функция активации в виде логистического сигмоида, обладающая всеми свойствами, необходимыми для нелинейности в нейронной сети: ограниченность (стремление к нулю при х → -∞ и к единице при х → ∞), дифференцируемость на всём диапазоне определения, малые вычислительные затраты на определение производной. Однако эксперименты Глоро и Бенджи с глубокими сетями с функцией активации в виде сигмоида, показали, что последний уровень сети очень быстро насыщается, и преодолеть эту ситуацию насыщения очень сложно [7].
Еще одной широко распространённой функцией активации является гиперболический тангенс. В отличие от сигмоида, функция гиперболического тангенса имеет более «крутые» характеристики в части нарастания и убывания выходного значения. При этом значение аргумента равное нулю является самой нестабильной промежуточной точкой, т.е. можно легко оттолкнуться от нуля и начать менять аргумент в любую сторону. Данный вид функции активации очень часто используется в области компьютерного зрения. Однако такие функции активации характеризуются недостаточно точным отражением состояния нейрона, т.е., по сути, они дают бинарный выходной сигнал, например активация нейрона «с силой 5» (для сигмоида выходное значение будет 0,9933) слабо отличается от активации «с силой 10» (выходное значение 0,99995). Позднее были разработаны такие функции, как логарифмическая и ReLU. Данные функции имеют сходные выходные характеристики. Однако для вычисления производной функции ReLU требуется лишь одно сравнение, то есть ReLU-сети при одних и тех же вычислительных затратах на обучение могут быть значительно больше по размеру.
Дальнейшее развитие этого направления – различные модификации и обобщения функции ReLU,– Leaky ReLU, Parameterized ReLU, ELU.
Результаты исследования и их обсуждение
Рассматривались следующие алгоритмы обучения: Backpropagation (MFE); quickProp; Rprop; Nesterov Accelerated Gradient (NAG); AdaDelta; Adam; NAdam. Точность работы алгоритмов оценивалась по абсолютной ошибке аппроксимации рассматриваемых функций в режиме онлайн-обучения нейронной сети при её стационарных параметрах, а также в составе адаптивной САУ [6–8]. В качестве параметров нейронной сети установлены: 1) количество слоев нейронной сети – 4; 2) количество нейронов в 1-м слое – 2; 3) количество нейронов в скрытых слоях – 10, 15 соответственно; 4) количество нейронов в выходном слое – 1; 5) дискретизация сети – 0,01 с; 6) функция активации в выходном слое – линейная. В качестве функций активации в скрытых слоях нейронной сети рассматривались три функции:
y = 1/(1 + exp(-s)); SoftPlusy = log(1 + exp(s)); ReLU if(s> = 0) y = s; elsey = 0.
В таблице представлены основные параметры алгоритмов обучения, используемые в процессе исследования.
Параметры алгоритмов обучения
|
Алгоритм обучения |
Сигмоидальная функция активации |
SoftPlus |
ReLU |
|
Backpropagation |
η = 0,5; μ = 0,1; ρ = 0 |
η = 0,5; μ = 0,1; ρ = 0 |
η = 0,5; μ = 0,1; ρ = 0 |
|
quickProp |
η = 0,8; μ = 0; ρ = 0 |
не стабилен |
η = 0,77; μ = 0; ρ = 0 |
|
Rprop |
η = 0,5;a = 1,01; b = 0,3 μ = 0; ρ = 0 |
η = 0,5;a = 1,01; b = 0,3 μ = 0; ρ = 0 |
η = 0,5;a = 1,01; b = 0,3 μ = 0; ρ = 0 |
|
NAG |
η = 0,5; m = 0,3; p = 0,5; μ = 0; ρ = 0 |
η = 0,5; m = 0,3; p = 0,5; μ = 0; ρ = 0 |
η = 0,5; m = 0,3; p = 0,5; μ = 0; ρ = 0 |
|
RMSprop |
η = 0,03; α = 0,4; μ = 0; ρ = 0 |
η = 0,03; α = 0,2; μ = 0; ρ = 0 |
η = 0,3; α = 0,2; μ = 0; ρ = 0 |
|
AdaDelta |
η = 0,5; μ = 0; ρ = 0 |
η = 0,5; μ = 0; ρ = 0 |
η = 0,5; μ = 0; ρ = 0 |
|
Adam |
η = 0,7; μ = 0; ρ = 0 |
η = 0,5; μ = 0; ρ = 0 |
η = 0,7; μ = 0; ρ = 0 |
|
NAdam |
η = 0,8; μ = 0; ρ = 0 |
η = 0,8; μ = 0; ρ = 0 |
η = 0,8; μ = 0; ρ = 0 |
На рис. 1–3 представлены ошибки обучения при аппроксимации функции вида y = Asin(ωt + φ) и различных функциях активации.
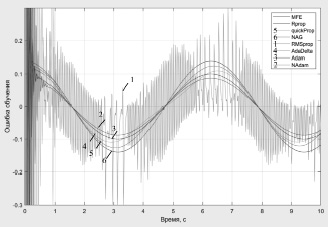
Рис. 1. Ошибки обучения нейронной сети при сигмоидальной функции активации
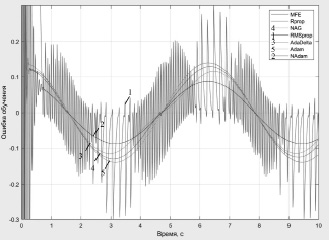
Рис. 2. Ошибки обучения нейронной сети при функции активации SoftPlus
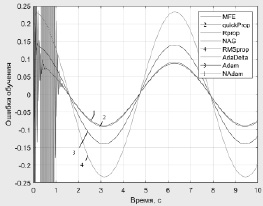
Рис. 3. Ошибки обучения нейронной сети при функции активации ReLU
Заключение
Результаты исследования показали, что рассматриваемые методы обладают примерно одинаковыми точностными характеристиками. Однако метод quickProp при использовании функции активации SoftPlus имел нестабильный характер процесса обучения, при этом варьированием параметров алгоритма не удалось обеспечить сходимость процесса обучения. При использовании метода RMSpropс функциями активации в виде сигмоиды и SoftPlus ошибки обучения имеет колебательный характер. В целом анализ результатов исследования свидетельствует о том, что методы Adam и NAdam с применением ReLU функции активации в скрытых слоях демонстрируют лучшие значения скорости сходимости обучения и меньшую вероятность застревания алгоритма в локальном минимуме, а также меньшие значения ошибки обучения. Наиболее целесообразным является использование метода NAdam.



