Считается, что спортивный судья обязан быть беспристрастным, особенно в том случае, когда его объективное суждение жизненно важно для спортсменов. Поэтому вопрос о том, принимают ли судьи предвзятые решения, и понимание причин, из-за которых судьи отступают от своей основной обязанности – беспристрастности, является фундаментальным не только с практической, но и с теоретической точки зрения. В то же время оценка распространенности этого явления и причин предвзятости судей имеет отношение к различным видам спорта. Предвзятость судей особенно актуальна в тех видах спорта, в которых субъективная предвзятость в принятии решений может определять результаты соревнований, что может иметь серьезные последствия для карьеры спортсменов [1], при этом эта предвзятость сохраняется даже при изменении системы оценки соревнований [2, 3].
С самого начала развития танцевального спорта пары на соревнованиях, так же как и в других видах спорта, оцениваются на основе определенных критериев и систем, которые с развитием танцевального спорта постоянно изменяются [4]. В настоящее время в зависимости от уровня соответствующего конкурса используются детально разработанные критерии, представляющие собой основные требования и параметры для оценки технических и артистических показателей танцевального выступления. Судьи оказывают ключевое влияние на конечный результат, показываемый спортсменами, как объективно, так и субъективно. В то же время, несмотря на все изменения, которые вносят в эти системы оценки эксперты WDSF, проблема объективной оценки выступлений спортсменов стоит все так же остро [5, 6]. Однако на соревнованиях по спортивным танцам на уровне отдельной страны, на которых используется старая система оценки спортсменов, присутствуют свои, хотя и менее заметные групповые идентичности, которые не могут быть так легко выявлены. В то же время факт, что общая групповая идентичность является определяющим фактором при принятии решений, хорошо согласуется с теоретической работой по идентификации и принятию индивидуальных решений [7].
В настоящее время в соревнованиях по танцевальному спорту применяются две системы – система «Skating» и новая система WDSF, которая используется для судейства на чемпионатах Европы и мира, а также GrandSlams и World Cups [8]. Система «Skating» включает в себя 11 правил [9]. В соответствии с этой системой танцевальные пары выступают в группах, и для участия в финале во время отборочных раундов общее количество пар уменьшается вследствие исключения пар, получивших самые низкие оценки. Существуют работы, в которых анализируются причины необъективности судейства в танцевальном спорте [7, 10]. Одной из таких причин считается то, что арбитры в танцевальном зачастую одновременно являются и тренерами, в связи с чем они могут судить на соревнованиях тренируемые ими пары («свои пары»). В то же время аналитические работы с результатами судейства соревнований, которые могли бы выявить реальную степень необъективности судейства и причины этого явления, в литературе отсутствуют.
Таким образом, целью настоящего исследования была попытка выявления статистической достоверности аномального судейства в финале соревнований по танцевальному спорту.
Материалы и методы исследования
Для достижения поставленной цели были проанализированы судейские протоколы финала соревнований по танцевальному спорту «Открытый международный фестиваль Танцевальные истории – 2019», проходивший в России, в г. Москве. При анализе 39 итоговых протоколов, в которых указаны тренеры спортсменов, были выделены две группы судей – имеющих на паркете тренируемые ими «свои пары» и не имеющих таковых, для которых все пары – «чужие пары». Результаты судейства в них были сгруппированы для каждой из пар, занявших первое, второе и третье места так, как показано на рисунке для наглядности выявления случаев аномального судейства, когда судья, к примеру, в пяти танцах дает паре все первые места.
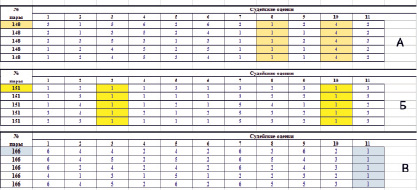
Сгруппированные по парам места, данные парам судьями в финале соревнований по результатам пяти танцев. А – «своя пара» № 148 для судьи № 8 заняла 1 место, Б – «своя пара» № 151 для судей № 3 и № 10 заняла второе место, В – «своя пара» № 166 для судьи № 11 заняла третье место. Судьи обозначены цифрами от 1 до 11. Цветом выделены случаи аномального судейства
Однако аномальное судейство, когда судья дает паре все первые места, как показано на рисунке, может происходить и по объективным причинам, в частности из-за того, что вследствие большого числа первых мест, данных всеми судьями паре, для конкретной пары вероятность такого судейства может быть достаточно высокой. В связи с этим нельзя априори определять такие случаи как несправедливые.
В связи с этим был проведен анализ вероятности такого судейства и его результаты сравнили с фактическими результатами судейства на соревнованиях. Для этого на основании данных, приведенных в первых столбцах таблиц (Отношение числа первых мест, данных паре, к общему числу выставленных ей оценок), при помощи формулы Бернулли (1), определяющей вероятность того, что в n независимых испытаниях будет ровно k раз наблюдаться событие, вероятность которого равна p:
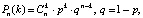 (1)
(1)
где p – вероятность возникновения события, 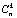 – количество сочетаний n по k [11].
– количество сочетаний n по k [11].
И формулы расчета полной вероятности события (2), когда вероятность события B равна сумме произведений вероятностей каждого из событий Ai на соответствующую условную вероятность события A:
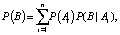 (2)
(2)
была рассчитана вероятность аномального судейства для чужих пар, занявших первое, второе и третье места.
Далее на основании этих данных рассчитывалось число случаев аномального судейства на судью в каждом случае, и на основании рассчитанных по описанным выше методикам данных для сравнения выборок проводился расчет t-критерия Стьюдента [12].
Результаты исследования и их обсуждение
Для расчета достоверности различий между этими вероятностями, прежде всего, были вычленены те финалы, в которых судьи имели занявшие вторые и третьи места «свои пары» на паркете (таковых было выявлено девять финалов – в пяти из них «свои пары» заняли второе место и в четырех заняли третье место), и те, в которых такие «свои пары» на паркете отсутствовали (шестнадцать финалов). Далее для них рассчитывалось отношение числа первых мест, данных паре, к общему числу выставленных ей оценок, данные которых далее были использованы для расчета числа теоретически возможных случаев аномального судейства и число случаев аномального судейства для этих пар, как абсолютное, так и в перерасчете на одного судью. Эти данные для варианта «чужие пары» приведены в табл. 1.
Таким образом были рассчитаны показатели аномального судейства в перерасчете на одного судью для судей, не имеющих на паркете своих пар, т.е. для варианта «чужие пары».
Для пар, занявших первое место, средняя арифметическая (М) числа случаев аномального судейства из расчета на одного судью составляла 0,62, а средняя ошибка средней арифметической (m) составляла 0,04 при числе единиц наблюдения (n): 14.
Для пар, занявших второе место, средняя арифметическая (М) числа случаев аномального судейства из расчета на одного судью составляла 0,03, а средняя ошибка средней арифметической (m) составляла 0,01 при числе единиц наблюдения (n): 14. Таким образом, при сравнении пар, занявших первые и вторые места, значение t-критерия Стьюдента равно 14,31 и, следовательно, различия между ними статистически значимы (p = 0,000000).
При этом для пар, занявших третье место, средняя арифметическая (М) числа случаев аномального судейства из расчета на одного судью составляла 0,00, а средняя ошибка средней арифметической (m) составляла 0,00 при числе единиц наблюдения (n): 14. Следовательно, при сравнении пар, занявших второе и третье места, значение t-критерия Стьюдента равно 3,00, в связи с чем различия между этими вариантами также статистически значимы (p = 0,006038).
Таким образом, для «чужих пар» наблюдается статистически достоверная разница между числом первых мест, выставленных в финале судьями, как между парами, занявшими первые и вторые места, так и между парами, занявшими вторые и третьи места, при высоком уровне значимости.
Далее был проведен аналогичный расчет для варианта «свои пары», занявшие вторые места в конечном зачете. Данные для этого варианта приведены в табл. 2.
Таблица 1
Отношение числа первых мест, данных паре, к общему числу выставленных ей оценок и число случаев аномального судейства для «чужих пар»
|
№ |
Число судей |
Отношение числа первых мест, данных паре, к общему числу выставленных ей оценок |
Число случаев аномального судейства |
|||||||
|
Пара, занявшая 1 место |
Пара, занявшая 2 место |
Пара, занявшая 3 место |
Пара, занявшая 1 место |
Пара, занявшая 2 место |
Пара, занявшая 3 место |
|||||
|
абсолютное |
На судью |
абсолютное |
На судью |
абсолютное |
На судью |
|||||
|
1 |
11 |
0,64 |
0,24 |
0,13 |
4 |
0,36 |
0 |
0,00 |
0 |
0,00 |
|
2 |
7 |
0,65 |
0,14 |
0,14 |
1 |
0,14 |
0 |
0,00 |
0 |
0,00 |
|
3 |
7 |
0,51 |
0,14 |
0,31 |
2 |
0,29 |
0 |
0,00 |
0 |
0,00 |
|
4 |
11 |
0,75 |
0,09 |
0,07 |
5 |
0,45 |
1 |
0,09 |
0 |
0,00 |
|
5 |
7 |
0,37 |
0,14 |
0,23 |
1 |
0,14 |
0 |
0,00 |
0 |
0,00 |
|
6 |
7 |
0,80 |
0,09 |
0,08 |
4 |
0,57 |
0 |
0,00 |
0 |
0,00 |
|
7 |
11 |
0,56 |
0,35 |
0,07 |
3 |
0,27 |
1 |
0,09 |
0 |
0,00 |
|
8 |
11 |
0,56 |
0,42 |
0,02 |
4 |
0,36 |
2 |
0,18 |
0 |
0,00 |
|
9 |
9 |
0,61 |
0,28 |
0,11 |
3 |
0,33 |
1 |
0,11 |
0 |
0,00 |
|
10 |
9 |
0,56 |
0,31 |
0,09 |
3 |
0,33 |
1 |
0,11 |
0 |
0,00 |
|
11 |
9 |
0,91 |
0,09 |
0,00 |
7 |
0,78 |
0 |
0,00 |
0 |
0,00 |
|
12 |
7 |
0,66 |
0,09 |
0,17 |
2 |
0,29 |
0 |
0,00 |
0 |
0,00 |
|
13 |
7 |
0,57 |
0,40 |
0,00 |
2 |
0,29 |
1 |
0,14 |
0 |
0,00 |
|
14 |
11 |
0,51 |
0,27 |
0,15 |
3 |
0,27 |
2 |
0,18 |
0 |
0,00 |
Таблица 2
Отношение числа первых мест, данных паре, к общему числу выставленных ей оценок и число случаев аномального судейства для «своих пар», занявших в конечном зачете второе место
|
№ |
Число судей |
Отношение числа первых мест, данных паре, к общему числу выставленных ей оценок |
Число случаев аномального судейства |
|||||||
|
Пара, занявшая 1 место |
Пара, занявшая 2 место |
Пара, занявшая 3 место |
Пара, занявшая 1 место |
Пара, занявшая 2 место |
Пара, занявшая 3 место |
|||||
|
абсолютное |
На судью |
абсолютное |
На судью |
абсолютное |
На судью |
|||||
|
1 |
7 |
0,49 |
0,26 |
0,09 |
1 |
0,14 |
1 |
0,14 |
0 |
0,00 |
|
2 |
7 |
0,17 |
0,40 |
0,00 |
1 |
0,14 |
1 |
0,14 |
0 |
0,00 |
|
3 |
9 |
0,33 |
0,39 |
0,14 |
1 |
0,11 |
1 |
0,11 |
1 |
0,11 |
|
4 |
7 |
0,57 |
0,43 |
0,00 |
3 |
0,43 |
1 |
0,14 |
0 |
0,00 |
|
5 |
7 |
0,40 |
0,40 |
0,00 |
1 |
0,14 |
2 |
0,29 |
0 |
0,00 |
На основании данных табл. 2 были рассчитаны следующие показатели аномального судейства в перерасчете на одного судью для судей, имеющих на паркете свои пары, занявшие в конечном зачете второе место: средняя арифметическая (М) числа случаев аномального судейства из расчета на одного судью составляла 0,16, а средняя ошибка средней арифметической (m) составляла 0,04 при числе единиц наблюдения (n): 5.
Сравнение «своих пар», занявших вторые места (среднее значение 0,16), с занявшими вторые места «чужими парами» (среднее значение 0,03) показало, что значение t-критерия Стьюдента в данном случае составляет 3,15 и различия между этими вариантами, соответственно, статистически значимы (p = 0,006157).
Таким образом, число первых мест, данных судьями «своим парам», занявшим вторые места, в пересчете на одного судью достоверно выше, чем данным «чужим парам», также занявшим вторые места.
Аналогичный расчет был проведен и для варианта «свои пары», занявшие третьи места в конечном зачете. Данные для этого варианта приведены в табл. 3. На основании данных табл. 3 были рассчитаны следующие показатели аномального судейства в перерасчете на одного судью для судей, имеющих на паркете свои пары, занявшие в конечном зачете третьи места: средняя арифметическая (М) числа случаев аномального судейства из расчета на одного судью составляла 0,16, а средняя ошибка средней арифметической (m) составляла 0.05 при числе единиц наблюдения (n): 4.
Таблица 3
Отношение числа первых мест, данных паре, к общему числу выставленных ей оценок и число случаев аномального судейства для «своих пар», занявших в конечном зачете третье место
|
№ |
Число судей |
Отношение числа первых мест, данных паре, к общему числу выставленных ей оценок |
Число случаев аномального судейства |
|||||||
|
Пара, занявшая 1 место |
Пара, занявшая 2 место |
Пара, занявшая 3 место |
Пара, занявшая 1 место |
Пара, занявшая 2 место |
Пара, занявшая 3 место |
|||||
|
абсолютное |
На судью |
абсолютное |
На судью |
абсолютное |
На судью |
|||||
|
1 |
11 |
0,61 |
0,11 |
0,18 |
4 |
0,36 |
0 |
0,00 |
2 |
0,18 |
|
2 |
11 |
0,58 |
0,09 |
0,33 |
4 |
0,36 |
0 |
0,00 |
3 |
0,27 |
|
3 |
11 |
0,62 |
0,13 |
0,22 |
4 |
0,36 |
0 |
0,00 |
1 |
0,09 |
|
4 |
11 |
0,45 |
0,31 |
0,15 |
1 |
0,09 |
2 |
0,18 |
1 |
0,09 |
Сравнение «своих пар», занявших третьи место (среднее значение 0,16), с занявшими третьи места «чужими парами» (среднее значение 0,00), показало, что значение t-критерия Стьюдента в данном случае составляет 3,20 и различия между этими вариантами, соответственно, также статистически достоверны (p = 0,005964). Таким образом, число первых мест, данных судьями «своим парам», занявшим третьи места, в пересчете на одного судью достоверно выше, чем у «чужих пар», также занявших третьи места.
В целом, сравнивая число первых мест, данных судьями «чужим парам», можно сделать вывод, что они ранжируются между парами, занявшими в результате первое, второе и третье места, как 1 > 2 > 3, причем различия между ними статистически значимы. В то же время, сравнивая места, данные судьями «чужим парам» и «своим парам», можно заключить, что «своим парам» судьи статистически достоверно выставляют более высокие места, чем «чужим парам».
Заключение
Данное статистическое исследование того, как наличие в финале соревнований на паркете «своих пар» влияет на оценки, выставляемые танцорам судьями, показывает, что наличие на паркете «своих пар» оказывает на судей непреодолимое воздействие, и они начинают судить аномально, большей частью не обращая внимания на фактическое качество исполнения танца танцорами, подсуживая при этом «своим парам» и засуживая при этом «чужие пары».
В то время как большая часть исследований в области исследования объективности судейства в танцевальном спорте была ранее сосредоточена на анкетировании как судей, так и спортсменов, исследование этого феномена при помощи математической статистики может помочь нам понять, какие организационные меры для активного воздействия на данный феномен необходимо принять в повседневной практике соревнований. По нашему мнению, прежде всего, такой мерой должен быть полный запрет на судейство в финале при наличии на паркете «своих пар».



