По определению параметр есть величина, значения которой позволяют различать элементы некоторого множества между собой. Рассмотрим, например, уравнения x = at – asint, y = a – acost. Видно, что каждому числу t, согласно этим равенствам, можно поставить в соответствие точку на плоскости с координатами (x, y). Множество всех таких точек, как известно, образует кривую, называемую циклоидой. Согласно приведенному определению, t следует назвать параметром.
При более общей трактовке понятия «параметр» некоторому числу или числам в соответствие ставится некоторый объект. Пусть, например,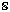 
– математическая модель (объект), структура которой задана, но некоторые величины, входящие в нее, заранее не определены. В простейших случаях модель 
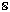с заданной структурой полностью определяется одним параметром λ, тогда говорят о семействе 
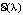. Таким образом, при этой трактовке понятия параметра каждому значению λ ставится в соответствие объект 
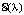, обладающий теми или иными свойствами, которые мы и изучаем при различных возможных изменениях λ. Объект может быть функцией (оператором, функционалом), системой уравнений или неравенств, пространственной кривой или поверхностью, совокупностью кривых на плоскости или в пространстве. Приведем простые примеры.
1. Пусть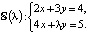 
Исследуйте решения системы в окрестности точки λ* = 6.
2. Пусть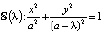 
. Изобразите всю совокупность кривых. Что с геометрической точки зрения отвечает параметру λ* = a?
3. Изобразите эскизы поверхностей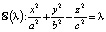 
. Что происходит при переходе через значение λ* = 0?
4. Пусть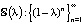 
. Каким λ отвечают сходящиеся последовательности?
5. Пусть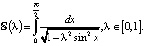 
Вычислите 
, 
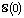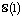. Докажите монотонность функции 
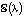в интервале 
.
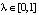6. Дано дифференциальное уравнение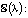 
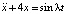. При каких λ решения уравнения ограничены (не ограничены)?
Целью настоящей статьи является построение методологии обучения математике в политехническом вузе, в центр которой предлагается ставить понятие семейства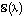 
математических моделей, зависящих от параметра. В целом для математики это не является новым. Новизна здесь в том, чтобы эта концепция проходила лейтмотивом через весь курс математики с акцентом на том, что наличие параметра (или параметров) в задаче вносит дополнительную особенность: требует повышенного внимания, оттачивает логику рассуждений, стимулирует интерес. Таким образом, рассмотрение таких задач способствует постепенному формированию у студентов исследовательских навыков [1–3]. Обратим внимание, что четко усвоенные алгоритмы решения задач и многочисленное их повторение на практике такой функции не решают, при этом притупляется сознание, а интерес у студентов пропадает. Задачи с параметрами можно ставить во всех разделах курса математики: алгебре, геометрии, анализе, теории вероятностей, но особенно в дифференциальных уравнениях и информатике. Последнее объясняется тем, что область исследования дифференциальных уравнений и отображений (так именуются дискретные динамические системы) с параметрами, называемая теорией бифуркаций, по существу, междисциплинарная и является краеугольным камнем современной нелинейной динамики, активно развивающейся в настоящее время [4–6]. В информатике рассмотрение таких задач дает возможность познакомить студентов с результатами, которые в науке были изучены сравнительно недавно. Здесь имеется в виду феномен детерминированного хаоса, открытого в 1970-х гг. [7, 8]. Подчеркнем, что параметр – это, с одной стороны, математический изыск, с другой – требование практики, и культуру работы с ним необходимо постепенно формировать и совершенствовать.
Разноуровневые исследовательские задачи
Прежде всего отметим, что параметры, входящие в математическую модель, выполняют разную роль. В одних задачах за ними скрываются числовые величины, изменение которых принципиально ничего не меняет в поведении модели, и это самое простое толкование параметра (в этом случае говорят о грубой модели [4]). При этом малым изменениям параметра отвечают малые изменения свойств в модели (в поведении системы). В других, принципиально иных задачах, параметр вводят в задачу специально, чтобы воспользоваться возникающими на этом пути возможностями в решении задачи [9]. В-третьих, параметр в исходной модели вовсе отсутствует, но появляется в процессе решения задачи [10–12]. В-четвертых, параметр отражает философский закон перехода количества в качество. А именно при переходе параметра через некоторое значение λ* модель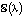 
изменяется качественно (в этом случае говорят, что модель не является грубой при λ*). Именно такие изменения являются предметом теории бифуркаций [4, 11]. Обсудить все возможные ситуации с достаточной полнотой в одной статье нам не удастся. Остановимся на некоторых отмеченных аспектах появления и использования параметра и расставим необходимые акценты.
Обсудим для начала идею введения параметра в математическую модель с целью решения задачи. Продемонстрируем метод на примерах из интегрального исчисления. Метод элементарен, познавателен и полезен как инструментарий многочисленных учебных заданий.
Пример 1. Требуется вычислить следующий несобственный интеграл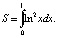 
С этой целью рассмотрим вспомогательный интеграл с параметром λ:
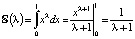
На первый взгляд, никакой связи между двумя интегралами нет. Однако, вычисляя последовательно производные по λ под знаком интеграла (данная операция здесь корректна), получим: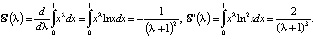 
Отсюда, полагая в последней формуле λ = 0, получим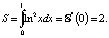 
Понятно, что на основе этой идеи вычисляются не только интегралы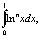 
но и другие.
Пример 2. Пусть требуется вычислить интеграл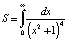 
. Мы знаем, что 
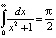. Рассмотрим его обобщение, 
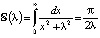. Дифференцируя последнее равенство по λ, легко находим 
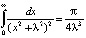. Дифференцируя еще раз, получим 
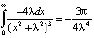. Отсюда находим 
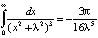. Дифференцируя третий раз, окончательно получаем 
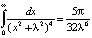. Таким образом, 
.
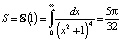Пример 3. Интеграл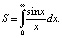 
Введем в рассмотрение параметр, обобщая наш интеграл 
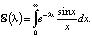Ясно, что 
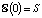. Продифференцируем 
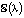по параметру 
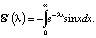Вычисляя последний интеграл по частям два раза, приходим к уравнению 
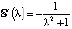. Отсюда, интегрируя, получим 
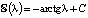. Для определения константы C перейдем в последнем равенстве к пределу при λ → +∞ и, учитывая, что 
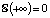, получим 
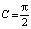. Тогда 
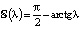. А тогда 
.
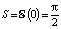Замечание. Идея искусственного введения параметра в модель с целью решения задачи используется в математике давно. Посмотрим на историческом примере [4], как в свое время она позволила разобраться с интегрированием уравнения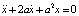 
(символы 
, 
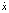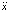обозначают 1-ю и 2-ю производные по t). Видно, что его характеристическое уравнение 
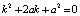имеет кратные корни 
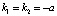и функция 
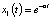– решение. Согласно теории, есть второе решение – линейно независимое с первым. Как же его нашли? Предположим, что корни характеристического уравнения были бы разные. Например, 
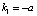и 
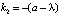. Здесь λ – малое число. Таким способом в задачу мы ввели параметр. Тогда вторым решением будет функция 
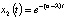. Но мы знаем из свойств решений линейных уравнений, что решением будет и комбинация 
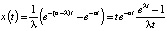. Переходя в этой последней формуле к пределу при λ ⟶ 0, получим 
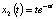. Таким образом, была найдена фундаментальная система решений 
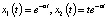дифференциального уравнения с кратными корнями.
Большие возможности для постановки учебно-исследовательских задач дает теория дифференциальных уравнений с параметрами. Начнем с задачи классификации типов положений равновесия линейных систем второго порядка. Постановка вопроса здесь предельно проста. Требуется дать классификацию положений равновесия в системе с параметром. Например, для системы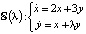 
провести разбиение прямой λ на промежутки с одинаковым поведением траекторий и изобразить все фазовые картины. Эта задача редуцируется к школьной – анализу квадратного уравнения с параметром λ [12] – и приведена в статье [13]. Ее можно отнести ко 2-му уровню сложности.
К задаче 3-го уровня сложности можно отнести следующую. Дано дифференциальное уравнение второго порядка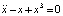 
и требуется найти решения, обладающие свойством 
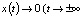). На первом шаге легко находится первый интеграл уравнения 
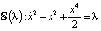. Заметим, что 
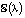есть семейство дифференциальных уравнений 1-го порядка. Затем на плоскости 
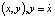строится семейство кривых 
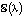. Далее необходимо сообразить, что искомое решение определяется значением параметра λ = 0, ибо уравнение 
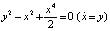задает инвариантное множество, проходящее через начало координат. Интегрируя последнее уравнение с начальными условиями 
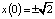, находим два искомых решения 
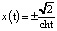. Обратим внимание, что параметр λ возник здесь естественным образом по ходу решения задачи. Другие подобные задачи приведены в статье [6].
Широкие возможности для постановки учебно-исследовательских задач предоставляет теория бифуркаций [4, 5, 13] – бурно развивающаяся сегодня отрасль нелинейной науки, имеющая многочисленные приложения в технике. Приведем несколько типовых задач такого плана, рассмотрение которых, с нашей точки зрения, является целесообразным.
Задача 1 сводится к бифуркационному анализу системы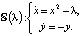 
Требуется исследовать ее по параметру как на плоскости x, y, так и в пространстве x, y, t. Заметим, что каждому значению параметра λ отвечает своя фазовая картина, т.е. множество «всех» траекторий на плоскости, отвечающих решениям x(t), y(t) системы. Причем при переходе через значение λ* = 0 фазовая картина качественно меняется, т.е. происходит бифуркация. Эта перестройка фазового портрета обсуждалась нами в статье [11]. При λ > 0 система имеет два состояния равновесия. Они являются устойчивым узлом и седлом. При λ* = 0 состояния равновесия сливаются в одно – полуустойчивое. При λ < 0 состояния равновесия исчезают. Такая бифуркация называется бифуркацией седла–узла. Эта задача может быть отнесена к первому уровню сложности, ибо уравнение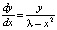 
легко интегрируется, и вся сложность ложится на анализ функции y(x, λ), зависящей от параметра.
Задача 2 знакомит с бифуркацией рождения предельного цикла из положения равновесия. Задача важна для многих технических специальностей (радиотехники, электроники, теории колебаний, теории регулирования). Модель имеет вид:
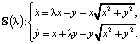
Учитывая специфику нелинейных членов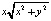 
и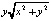 
, в этой системе целесообразно перейти к полярной системе координат, в которой система примет вид:
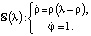
Решениями последней являются функции φ = t, ρ = ρ(t). Видно, что при λ < 0 функция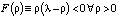 
. Стало быть, 
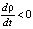и ρ(t), монотонно убывая, стремится при t → +∞ к единственному состоянию равновесия. При λ = 0 картина принципиально не изменяется (рекомендуется проинтегрировать соответствующие уравнения и разобраться с тонкостями стремления ρ(t) к нулю). При λ > 0 в системе возникает еще одно стационарное решение ρ = λ, которому на плоскости отвечает замкнутая траектория – окружность радиуса r = λ. При этом другие траектории стремятся к ней, навиваясь снаружи и изнутри (рис. 1). Это следует из анализа знака производной F'(λ).
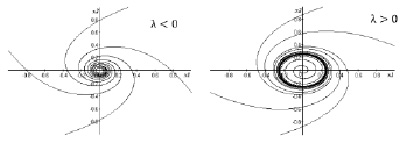
Рис. 1. Бифуркация рождения цикла
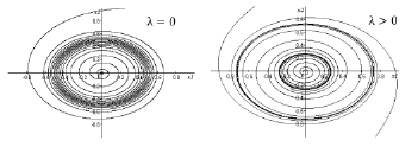
Рис. 2. Из сгущения траекторий (слева) рождаются два цикла (справа)
Задача 3 описывает бифуркацию рождения двух циклов – устойчивого и неустойчивого [14] из полуустойчивого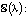 
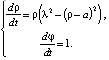(a – число).
Запишите эту систему в декартовой системе координат. Проверьте, что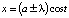 
, 
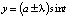– ее периодические решения, которым отвечают циклы. Проверьте, что при λ < 0 все траектории при t → +∞ спиралевидно наматываются на состояние равновесия ρ = 0. При λ = 0 возникает полуустойчивый цикл ρ = a: с одной стороны, траектории наматываются на цикл, с другой – сматываются с него (при t → +∞). При λ > 0 полуустойчивый цикл расщепляется на два: один устойчивый, т.е. притягивающий к себе траектории, другой (внутренний) – отталкивающий от себя траектории. Решение требуется дополнить фазовыми картинами, прибегнув к численному моделированию системы на ПК [15, 16] (рис. 2).
В задаче 4 требуется установить все бифуркации, среди которых новой является бифуркация рождения цикла из петли сепаратрисы седлового положения равновесия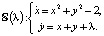 
Здесь требуется провести подробные аналитические вычисления, установить все бифуркационные значения параметра и провести компьютерные эксперименты для визуализации фазовых картин. Краткий анализ этой модели дан в статье [13].
Замечание. В приведенных выше задачах мы ограничились случаем одного параметра. Если в модели параметров больше, то их исследование существенно усложняется [4].
В курсе информатики к задачам высокого уровня сложности отнесем задачу численного исследования дискретного уравнения [7]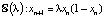 
. Несмотря на внешнюю простоту, эта математическая модель таит массу интересных эффектов. Феномен этой модели хорошо известен ученым (каскад бифуркаций удвоения периода, переход к хаосу). Однако численный анализ этой модели сегодня вполне посилен современному любознательному студенту. Таких дискретных моделей в современной математике и ее приложениях известно много. С ними можно ознакомиться по книгам [7, 8].
Вскользь коснемся понятия параметра, используемого в теории вероятностей. Хорошо известно, что закон распределения случайной величины ξ (как дискретной, так и непрерывной) задается функцией (распределения), включающей в себя постоянные величины – параметры, которые конкретизируются по ходу решения задачи. Так, например, для случайной величины, равномерно распределенной в замкнутом промежутке [a, b], числа a и b – суть параметры распределения; геометрическое распределение характеризуется одним числом p – вероятностью успеха в серии одинаковых испытаний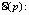 
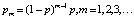; биномиальное распределение характеризуется уже двумя параметрами: числом независимых испытаний n и вероятностью успеха p: 
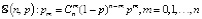; закон Пуассона 
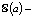одним – средним значением 
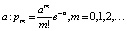; показательное распределение – также одним 
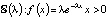; нормальный закон – двумя σ и m – среднеквадратическим отклонением и математическим ожиданием 
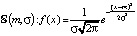. Мы считаем, вполне посильной, но сложной задачей доказательство предельной теоремы Пуассона: 
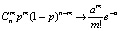(где p ≪ 1, n ≫ 1, np = a). Отметим, что распределение с двумя параметрами переходит в распределение с одним параметром [17].
Заключение
Древнейшая из наук математика за многовековую историю своего существования превратилась поистине в необъятную область человеческого знания, представимую сегодня конгломератом математических наук. Она востребована как никогда ранее, а возникающие прикладные задачи постоянно стимулируют ее развитие. Большие возможности открываются у математики в союзе с компьютерными методами и технологиями. Возросла роль дискретной математики. Вместе с тем преподавание общих курсов математики в технических вузах в сравнении с преподаванием других наук достаточно консервативно. Это объясняется фундаментальностью ее открытий, практической значимостью результатов ее применения и, к сожалению, временными рамками преподавания. Менять содержание и объемы излагаемого материала – дело опасное и ответственное, и это все хорошо понимают. Однако методик изложения математики во втузах существует множество в силу индивидуальных психологических различий и умственных способностей учащихся.
В настоящей статье мы обратились к анализу понятия «параметр», его сущности, предназначению и коснулись некоторых аспектов его применения. Заметим, что уровень профессионализма современного инженера в значительной степени определяется его умением оценивать влияние той или иной величины, присутствующей в математической модели, на ход протекания процесса или явления, т.е. работой с параметром (параметрами). В связи с этим особое положение здесь занимают математические модели, демонстрирующие ветвление (бифуркационные явления). С нашей точки зрения, элементы теории бифуркаций должны быть шире представлены в курсах математики втузов, подкреплены прикладными задачами из механики, физики, химии, экологии, экономики и иных, а понятию «параметр» в целом должно быть уделено большее внимание. Наша педагогическая практика многократно подтверждала, что математическое инженерное образование должно опираться на систему задач, среди которых важнейшее место следует отвести задачам с параметрами. Такие задачи наилучшим образом мотивируют студентов к обучению, формируют в них гибкость и креативность мышления. В силу сказанного мы и решили обратиться к этой теме.