Задача поиска и распознавания объектов с применением средств технического зрения сводится, как правило, к сравнению полутоновых описаний объекта с его эталоном, которое может быть выполнено различными способами [1]. Эталонные описания могут быть иерархическими, т.е. представляться в виде взаимосвязанных уровней. Например, изображения ригидных объектов в системах трехмерного моделирования полетов летательных аппаратов представляют в виде «пирамиды видимости» (viewing frustum) [2, 3], в которой первая иерархия (нижняя часть пирамиды) является наиболее полным описанием, далее изображение последовательно «сжимается» от слоя к слою по определенному правилу, что соответствует моделям изображения, наблюдаемого с разных расстояний.
Препятствием к распознаванию служат возможные изменения положения наблюдаемого объекта и его освещенности (яркости и контрастности), поэтому важным вопросом является инвариантность иерархических описаний к различным помехам и изменениям ракурса. Для нивелирования влияния сдвигов, поворотов и масштабирования целесообразно применять инвариантные моменты. Моменты имеют достаточно продолжительную историю, но продолжают эффективно использоваться в задачах распознавания образов [4, 5].
Для распознавания графического объекта, наблюдаемого системой технического зрения и представленного в базе данных иерархией полутоновых изображений, необходимо уметь проводить сравнение иерархий и определять расстояние между ними. Вопросы корректного сравнения иерархий рассмотрены в работе [6], в которой предложена специальная мера, основанная на схеме динамического программирования. В настоящей работе предлагаются подходы к решению проблем освещенности и корректного сравнения эталонных моделей с реальными изображениями объектов, представленных иерархиями.
Исследование направлено на построение и экспериментальное исследование метода сравнения объекта, видимого системой технического зрения, с эталонными изображениями, представленными в базе данных моделирующей системы. Особенностью подхода является представление всех объектов сцены в виде иерархий на основе слоев пирамид видимости, следовательно, необходимо уметь проводить сравнение иерархий и определять расстояние между ними. В основе сравнения лежит представление уровней иерархии сравниваемых объектов в виде наборов инвариантных моментов, обеспечивающих сжатие изображений и инвариантность к группе аффинных преобразований. Важной составляющей является вычисление расстояний между объектами специальным методом поиска минимального расстояния на основе одной из схем динамического программирования. Таким образом, целью исследования является построение работоспособного метода сравнения пирамид видимости объектов с эталонными пирамидами при условии снятия проблем освещенности, поворотов и сдвигов. Корректное сравнение эталонных моделей с реальными изображениями объектов, представленных иерархиями, в свою очередь лежит в основе распознавания объектов сцены в процессе траекторного движения летательного аппарата на основе эффективной процедуры сравнения с низкой вычислительной сложностью.
Материалы и методы исследования
1. Построение инвариантного эталона дальностного изображения
Для полутоновых моделей имеется набор инструментальных средств преобразования и распознавания, однако для их применения требуется нормирование яркости. Проблема освещенности решается переходом к дальностному изображению, применяемому в современных системах технического зрения.
Дальностное изображение – это цифровое изображение, у которого функция интенсивности d(i, j) в каждой точке изображения (x, y) принимает целые значения, равные расстоянию r до точки наблюдения [7]. Пусть задано максимальное целочисленное расстояние M, определяющее максимальную глубину наблюдения объекта системой технического зрения. В точках, для которых расстояние r > M, d(x, y) = 0, таким образом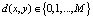 
. Дальностному изображению можно поставить в соответствие полутоновое изображение с функцией яркости p(x, y), которая принимает целые значения от 0 до B – 1, где B = 256. Таким образом, можно перейти к псевдополутоновому описанию, которое непосредственно не зависит от яркости. Недостаток подхода – необходимость иметь устройства измерения дальности. Это могут быть лазеры или ультразвуковые приборы. Не останавливаясь на этой проблеме, будем рассматривать распознавание полутоновых объектов, не зависящих от изменения яркости и контрастности.
2. Принципы сравнения иерархий
Вопросы пирамидального представления изображений и их сравнения (analytic hierarchy process) и идентификации рассмотрены, например, в работах [2, 6]. Отдельные вопросы сравнения иерархий рассматриваются в материалах [8]. Здесь можно рассмотреть два подхода, отличающиеся применяемыми метриками и способом представления данных.
Первый непосредственно связан с технологией сравнения иерархий в соответствии с работой [6]. Пусть, например, известны изображения наблюдаемого объекта с разных расстояний, увязанных в пирамиду. Попробуем сравнить его с проекцией 3D эталона, некоторого общего положения. Для этого представим изображение в виде графа – упорядоченного облака точек. Пусть, например, каждая точка характеризуется только одним значением (глубины, псевдояркости). Граф получаем путем развертки изображения по принципу растровой развертки «сверху вниз» и «слева направо». Первым шагом в процедуре является нахождение матрицы локальных расстояний d(i, j) между иерархиями эталона и текущего объекта. Сравнение уровней производится поиском похожих пар вершин, где каждая вершина является точкой изображения, которой приписаны координаты и «дальность». Пусть, например, уровень i первой иерархии сравнивается с уровнем j второй иерархии. Последовательно сравниваем каждую вершину первой иерархии с вершинами второй иерархии и находим похожую по весу вершину на выбранных уровнях. Затем находим расстояние между вершинами (как модуль разности весов). Разности между похожими вершинами заносим в счетчик и суммируем. Если для вершины нет пары, то вводим дополнительные вершины с нулевым весом. Полученное значение счетчика с минимальной суммой заносится в соответствующую ячейку таблицы. После заполнения таблицы в ней содержатся величины локальных расстояний между всеми парами уровней иерархий. Расстояние между иерархиями двух объектов соответствует «стоимости» оптимального перевода уровней иерархии первого объекта в соответствующие уровни иерархии второго объекта. Для этого перевода используем методы динамического программирования. Движение от верхней левой клетки к нижней правой клетке таблицы осуществляется по диагонали, горизонтали и вертикали. В проложенном пути производим суммирование чисел, находящихся в клетках, входящих в оптимальный путь. При этом учитываются дополнительно весовые коэффициенты перехода по горизонтали, вертикали и диагонали соответственно. Для определенности будем пользоваться схемой, когда по диагонали движение осуществляется с коэффициентом 1, а по вертикали и горизонтали с коэффициентом 2 (по схеме 2–1–2). В случае неоднозначности движения по клеткам для измерения расстояния следует рассмотреть все альтернативные пути. В качестве простейшего примера построим пирамиду видимости для полутонового изображения, представленного матрицей значений пикселей размером 4х4 (рис. 1).
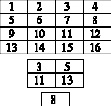
Рис. 1. Пример пирамиды видимости для полутонового изображения
Пирамида видимости отражает уровни детализации. Пример построения иерархического представления приведен на рис. 2.
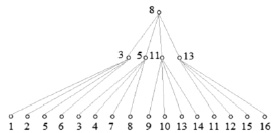
Рис. 2. Иерархическое представление изображения 4х4
3. Сравнение изображений на основе инвариантов
Рассмотрим метод сравнения иерархий, альтернативный к рассмотренному выше методу. Промежуточным этапом является получение инвариантных моментов для каждой иерархии объекта, что приводит к следующим положительным эффектам: одинаковой размерности сравниваемых изображений; существенному сокращению размерности описаний сравниваемых объектов; нивелированию возможных искажений, связанных с поворотами и смещениями изображений.
Предлагается воспользоваться инвариантами Ху [9, 10]. Пусть функция яркости f(x, y) принимает значение с плавающей точкой от 0 до 1. Вначале проведем вычисление величин
, 
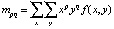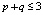, f(x, y),
где (x, y) – координаты точки, f(x, y) – яркость точки.
Средние значения:
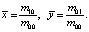
Рассмотрим поэтапно вычисление инвариантных моментов.
1 этап: Получение центральных моментов
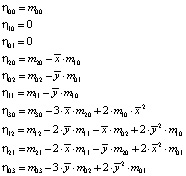
2 этап: Переход к формулам для инвариантных моментов
1) вычисляем все величины:
,
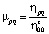где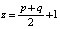 
;
2) получение моментов, инвариантных к операциям поворота, переноса и масштаби- рования:
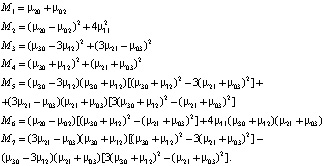
Результаты исследования и их обсуждение
Далее представлены полученные экспериментальные данные. Пусть даны три полутоновых объекта, изображения которых размерности 639 x 472 образуют первый уровень иерархии. На базе этих объектов могут быть получены изображения других уровней пирамиды видимости по принципу последовательного «сжатия». Уровни пирамиды видимости для каждого объекта представлены в табл. 1 (всего по семь уровней), для наглядности они приведены в одном масштабе.
Таблица 1
Исходные графические объекты
|
Объект 1 (Эйфелева башня) |
Объект 2 (Кремль) |
Объект 3 (Крымский мост) |
|
|
|
|
|
639 x 472 |
||
|
|
|
|
|
320 x 236 |
||
|
|
|
|
|
160 x 118 |
||
|
|
|
|
|
80 x 59 |
||
|
|
|
|
|
40 x 30 |
||
|
Окончание табл. 1 |
||
|
Объект 1 (Эйфелева башня) |
Объект 2 (Кремль) |
Объект 3 (Крымский мост) |
|
|
|
|
|
20 x 15 |
||
|
|
|
|
|
10 x 8 |
||
Инвариантные моменты для полученных слоев (уровней иерархии) изображения внесены в табл. 2. В таблицу не включены моменты М1, которые обычно используются для измерения расстояний до известных объектов (M1 = r∙h = const, где r – размер видимого изображения, h – расстояние до объекта).
Таблица 2
Расчет инвариантных моментов
|
Уровни |
Инвариантные моменты для изображений |
||
|
Первый объект |
Второй объект |
Третий объект |
|
|
1 (639 x 472) |
9.3976e-02 7.8943e-04 5.6717e-04 2.0075e-07 -7.7095e-05 3.2207e-07 |
8.2227e-02 2.4902e-03 1.1548e-03 -1.2724e-06 -6.7270e-05 1.4885e-06 |
9.0056e-02 2.3284e-03 2.5347e-03 6.0836e-06 -6.3594e-04 -9.5224e-07 |
|
2 (320 x 236) |
9.4928e-02 7.7041e-04 5.6738e-04 2.1076e-07 -7.3733e-05 3.1032e-07 |
8.3059e-02 2.4785e-03 1.1515e-03 -1.2659e-06 -6.7994e-05 1.4770e-06 |
9.1032e-02 2.3003e-03 2.5202e-03 5.9983e-06 -6.3611e-04 -9.1791e-07 |
|
3 (160 x 118) |
9.5162e-02 6.9756e-04 5.5662e-04 2.2471e-07 -6.3840e-05 2.6420e-07 |
8.3033e-02 2.4769e-03 1.1373e-03 -1.1892e-06 -7.5499e-05 1.4933e-06 |
9.1373e-02 2.2292e-03 2.5307e-03 5.9351e-06 -6.3782e-04 -9.5030e-07 |
|
4 (80 x 59) |
9.5498e-02 6.5512e-04 5.6365e-04 2.6840e-07 -4.8844e-05 2.1279e-07 |
8.3087e-02 2.5135e-03 1.1057e-03 -1.0431e-06 -8.9350e-05 1.5199e-06 |
9.1723e-02 2.0912e-03 2.5509e-03 5.8116e-06 -6.4345e-04 -9.6826e-07 |
|
5 (40 x 30) |
8.8721e-02 3.8116e-04 5.1909e-04 2.1703e-07 -2.7237e-05 7.8815e-08 |
7.4773e-02 2.6425e-03 1.0901e-03 -6.9596e-07 -1.2476e-04 1.7144e-06 |
8.3208e-02 2.1236e-03 2.7022e-03 6.3549e-06 -6.4283e-04 -1.2308e-06 |
|
6 (20 x 15) |
8.9320e-02 3.8594e-04 5.1911e-04 2.1976e-07 -2.4991e-05 7.5457e-08 |
7.5170e-02 2.6777e-03 1.0986e-03 -7.0216e-07 -1.2594e-04 1.7487e-06 |
8.3806e-02 2.1518e-03 2.7230e-03 6.4871e-06 -6.5242e-04 -1.1674e-06 |
|
Окончание табл. 2 |
|||
|
Уровни |
Инвариантные моменты для изображений |
||
|
Первый объект |
Второй объект |
Третий объект |
|
|
7 (10 x 8) |
5.8582e-02 4.2102e-04 4.8924e-04 2.1442e-07 -3.5690e-05 5.7653e-08 |
4.6629e-02 3.1866e-03 1.3313e-03 -1.8914e-07 -1.6599e-04 2.7356e-06 |
5.3794e-02 2.8490e-03 3.4106e-03 1.0473e-05 -6.6328e-04 -1.8308e-06 |
В табл. 3–5 – расстояния между всеми парами изображений трех объектов по метрике Евклида на основе вычисленных инвариантных моментов.
Таблица 3
Расстояния между уровнями первого и второго объектов
|
Уровни объекта 1 |
Уровни объекта 2 |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
1.1886e-02 |
1.1062e-02 |
1.1087e-02 |
1.1038e-02 |
1.9300e-02 |
1.8908e-02 |
4.7414e-02 |
|
2 |
1.2830e-02 |
1.2006e-02 |
1.2031e-02 |
1.1981e-02 |
2.0249e-02 |
1.9857e-02 |
4.8366e-02 |
|
3 |
1.3072e-02 |
1.2248e-02 |
1.2006e-02 |
1.2223e-02 |
2.0489e-02 |
2.0097e-02 |
4.8603e-02 |
|
4 |
1.3410e-02 |
1.2586e-02 |
1.2611e-02 |
1.2561e-02 |
2.0828e-02 |
2.0436e-02 |
4.8941e-02 |
|
5 |
6.8567e-03 |
6.0706e-03 |
6.0931e-03 |
6.0522e-03 |
1.4142e-02 |
1.3756e-02 |
4.2193e-02 |
|
6 |
7.4260e-03 |
6.6321e-03 |
6.6551e-03 |
6.6127e-03 |
1.4733e-02 |
1.4347e-02 |
4.2791e-02 |
|
7 |
2.3745e-02 |
2.4572e-02 |
2.4545e-02 |
2.4602e-02 |
1.6353e-02 |
1.6752e-02 |
1.2299e-02 |
Расстояние между иерархиями объектов 1 и 2 по схеме 2–1–2 динамического программирования составит
R12 = 1.1886e-02 + 1.2006e-02 + 1.2006e-02 + 1.2561e-02 + 1.4142e-02 + + 1.4347e-02 + 1.2299e-02 = 8.9247e-2
Таблица 4
Расстояния между уровнями первого и третьего объектов
|
Уровни объекта 1 |
Уровни объекта 3 |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
4.6818e-03 |
3.8830e-03 |
3.6078e-03 |
3.3209e-03 |
1.1073e-02 |
1.0500e-02 |
4.0339e-02 |
|
2 |
5.5093e-03 |
4.6530e-03 |
4.3516e-03 |
4.0346e-03 |
1.2003e-02 |
1.1427e-02 |
4.1289e-02 |
|
3 |
5.7423e-03 |
4.8796e-03 |
4.5746e-03 |
4.2527e-03 |
1.2242e-02 |
1.1666e-02 |
4.1527e-02 |
|
4 |
6.0539e-03 |
5.1796e-03 |
4.8691e-03 |
4.5409e-03 |
1.2575e-02 |
1.1999e-02 |
4.1863e-02 |
|
5 |
3.1636e-03 |
3.6608e-03 |
3.8565e-03 |
4.0553e-03 |
6.2100e-03 |
5.7036e-03 |
3.5139e-02 |
|
6 |
2.9580e-03 |
3.3124e-03 |
3.4690e-03 |
3.6318e-03 |
6.7471e-03 |
6.2268e-03 |
3.5735e-02 |
|
7 |
3.1603e-02 |
3.2573e-02 |
3.2910e-02 |
3.3252e-02 |
2.4791e-02 |
2.5389e-02 |
6.1443e-03 |
R13 = 4.6818e-03 + 4.6530e-03 + 4.5746e-03 + 4.5409e-03 + 6.2100e-03 + + 6.2268e-03 + 6.1443e-03=3.70314e-2
Таблица 5
Расстояния между уровнями второго и третьего объектов
|
Уровни объекта 2 |
Уровни объекта 3 |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
7.9711e-03 |
8.9300e-03 |
9.2702e-03 |
9.6230e-03 |
1.9551e-03 |
2.3259e-03 |
2.8531e-02 |
|
2 |
7.1563e-03 |
8.1114e-03 |
8.4508e-03 |
8.8033e-03 |
1.6981e-03 |
1.8645e-03 |
2.9361e-02 |
|
3 |
7.1841e-03 |
8.1390e-03 |
8.4784e-03 |
8.8308e-03 |
1.7107e-03 |
1.8845e-03 |
2.9335e-02 |
|
4 |
7.1370e-03 |
8.0910e-03 |
8.4305e-03 |
8.7833e-03 |
8.7833e-03 |
1.8923e-03 |
2.9391e-02 |
|
5 |
1.5363e-02 |
1.6334e-02 |
1.6676e-02 |
1.7030e-02 |
8.6198e-03 |
9.2085e-03 |
2.1114e-02 |
|
6 |
1.4968e-02 |
1.5938e-02 |
1.6281e-02 |
1.6635e-02 |
8.2316e-03 |
8.8192e-03 |
2.1508e-02 |
|
7 |
4.3455e-02 |
4.4430e-02 |
4.4773e-02 |
4.5126e-02 |
3.6624e-02 |
3.7221e-02 |
7.4848e-03 |
R23 = 7.9711e-03 + 8.1114e-03 + 8.4784e-03 + 8.7833e-03 + + 2*(8.7833e-03 + 1.8923e-03 + 9.2085e-03 + 8.8192e-03) + 7.4848e-03 = 9.82356e-2.
Таким образом, наиболее близкими являются изображения 1 и 3 с наименьшим расстоянием R13 = 3.70314e-2. В данном случае проверка показывает, что расстояния соответствуют требованиям метрики (правило треугольника).
Утверждение: расстояние между иерархиями по установленной схеме сравнения является метрикой.
Доказательство этого утверждения лежит вне настоящей работы и может выполнено с использованием подходов, изложенных в работах [11, 12].
Нетрудно проверить, что расстояние между двумя идентичными объектами равно нулю, R11 = 0 + 0 + 0 = 0. Так для объекта на рис. 1 имеем ситуацию, представленную в табл. 6.
Таблица 6
Измерение расстояний между иерархиями
|
Иерархии Изображения на рис. 1 |
1 |
2 |
3 |
|
|
1 |
0 |
104 |
128 |
|
|
2 |
104 |
0 |
24 |
|
|
3 |
128 |
24 |
0 |
Аналогичная ситуация имеет место и для других рассмотренных полутоновых изображений.
Заключение
В ходе выполненного исследования рассмотрены инструментальные средства, предназначенные для корректного сопоставления пирамид видимости объектов как иерархических структур. Совмещение и сравнение пирамид (3D-моделей объектов) показывает, что здесь хорошо работают инвариантные моменты, которые существенно сжимают слои (уровни) объектов и приводят их к одной размерности, что позволяет использовать расстояние Евклида. Применение инвариантов и схемы динамического программирования упрощает построение систем распознавания объектов на трехмерных сценах.
Работа выполнена при финансовой поддержке следующих проектов РФФИ: 18-29-03011-мк и 20-07-00022-а.