Методы оптимизации и линейного программирования берут свое начало в 1820 г., когда Фурье предложил метод направленного перебора смежных вершин в направлении возрастания целевой функции – симплекс-метод, ставший на долгое время основным при решении задач линейного программирования [1]. Позднее в 1947 г. метод был расширен и дополнен американским ученым Джоржем Данцигом. Класс экстремальных задач, определяемых линейным функционалом на множестве, задаваемом линейными ограничениями, относят к 1930-м гг., когда появились первые разработки по решению задач линейного программирования исследователей Джона фон Неймана, Л.В. Канторовича [2, 3]. Тем же Канторовичем совместно с М.К. Гавуриным в 1949 г. был разработан метод потенциалов, являвшийся модификацией симплекс-метода решения задачи линейного программирования применительно к транспортной задаче. В последующих работах Л.В. Канторович, В.С. Немчинов, В.В. Новожилов, А.Л. Лурье, А. Брудно развили математическую теорию линейного и нелинейного программирования, в том числе развивая приложения к этой теории. В целом, в связи с развитием электронно-вычислительных средств и компьютерной техники, начиная с 1955 г. опубликовано множество работ как в области нелинейного программирования, так и в области квадратичного программирования (работы Баранкина, Дорфмана и пр.) [4, 5].
Актуальным вопросом при исследовании сложных систем зачастую становится задача упрощения сложных звеньев более простыми. В частности, сложный объект управления с большим количеством обратных связей – судовой главный двигатель – зачастую необходимо упростить или заменить более простым звеном.
Авторами была сформулирована цель исследования – рассмотреть и проанализировать возможность программной реализации метода роя частиц (МРЧ) в задаче аппроксимации сложного динамического звена простым апериодическим звеном второго порядка.
Материалы и методы исследования
Для рассмотрения передаточной функции топливной аппаратуры необходимо рассмотреть принцип произведения впрыска в судовом главном двигателе с электронным управлением подачей топлива типа MAN B&W xSxx ME-C. Принцип действия топливной аппаратуры раскрывает рис. 1 [6]. На последних моделях двигателей MAN B&W серии ME-C в качестве гидравлического блока цилиндра используется гидравлический блок HCU (Hydraulic cylinder unit), состоящий из топливного насоса высокого давления (ТНВД), исполнительного механизма выпускного клапана, гидравлического аккумулятора, лубрикатора цилиндра, электрогидравлического клапана корректировки подачи топлива, блока распределения гидравлики, трубопроводов, а также датчиков положения механизмов.
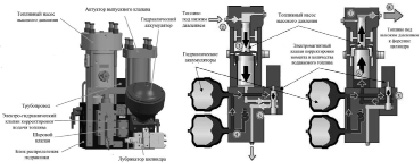
Рис. 1. Устройство и принцип действия блока HCU двигателя MAN B&W 6S90 ME-C
Рис. 2. Структурная схема контура подготовки топлива и клапана FIVA
Таким образом, в данном случае процесс подачи топлива можно представить в виде нескольких систем уравнений: уравнений работы электромеханической части электромагнитного клапана корректировки, уравнений работы гидравлической части электромагнитного клапана корректировки, уравнений работы распределителя гидравлики с трубопроводами, а также уравнений ТНВД с форсункой (рис. 2).
Положим эквивалентную передаточную функцию сложного звена равной
Wтопл(s) =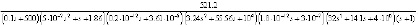 
Тогда целевой задачей является аппроксимация звена Wтопл(s) звеном:
Wэкв(s) =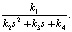 
Алгоритм роя частиц декларирует в своем составе рой одинаковых с точки зрения выполняемой функции частиц, обладающих положением и скоростью в текущий момент времени. Такими же свойствами обладает и весь рой в целом. Решение задачи оптимизации сводится к поиску оптимального положения частицы в n-мерном пространстве поиска решения посредством определения текущей ошибки положения частицы, вычисления скорости частицы, а также соответствующих свойств роя.
Корректировка скоростей и положений каждой из частиц в изначальной конфигурации производилась в соответствии с формулами [7]:
;
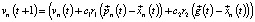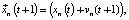
где vn(t + 1) – скорость частицы n в момент времени (t + 1), vn(t) – скорость частицы в текущий момент времени t, c1 = const – когнитивная весовая доля, r1 = const – случайная переменная в диапазоне [0;1],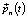 
– векторная величина, описывающая лучшее положение частицы, найденное на данный момент, 
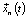– текущая позиция частицы, 
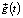– лучшая известная позиция, найденная для любой из частиц в рое, 
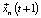– положение частицы n в момент времени (t + 1).
Текущая задача была решена на основе приложения, написанного на языке Visual C#. Для этого целесообразно рассмотреть алгоритм решения поставленной задачи при помощи рис. 3.
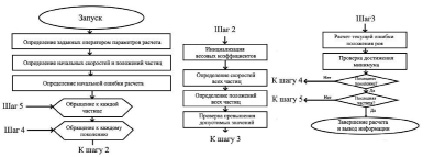
Рис. 3. Алгоритм решения задачи поиска минимума функции по методу роя частиц
Алгоритм берет свое начало с процедуры определения заданных оператором параметров расчета. Среди них – количество эпох расчета для каждого шага времени t, количество частиц n, размерность пространства поиска решений, а также максимально допустимые значения искомых параметров. Следом производится расчет начального положения частиц и их скоростей, исходя из значений которых определяется текущая ошибка расчета:
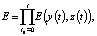
где y(t) и z(t) – временные зависимости заданной и искомой временной характеристики.
Далее инициализируется основной цикл обращения к каждой частице, содержащий в своем составе еще несколько циклов и основные операции, а именно: определение скоростей и положений всех частиц в последующие моменты времени, определение ошибок всех рассчитанных положений и проверки на превышение максимально допустимых текущими параметрами значений. Рассмотрим реализацию поставленной задачи подробнее.
В основу работы приложения заложен метод, реализующий инициализацию роя частиц, описание их свойств, расчет текущих скоростей и положений и определение ошибки положения каждой частицы и всего роя, который представляет собой код [8, 9]:
1 private void button2_Click(object sender, EventArgs e)
2 {
3 Random ran = null;
4 ran = new Random(0);
5 try
6 {
7 Particle[] swarm = new Particle[numberParticles];
8 double bestGlobalFitness = double.MaxValue;
9 double minV = -1.0 * maxX;
10 double maxV = maxX;
11 for (int i = 0; i < swarm.Length; ++i) 30 {
12 double[] randomPosition = new double[Dim];
13 for (int j = 0; j < randomPosition.Length; ++j)
14 {
15 double lo = minX;
16 double hi = maxX;
17 randomPosition[j] = (hi - lo) * ran.NextDouble() + lo;
18 }
19 double fitness = ObjectiveFunction(randomPosition);
20 double[] randomVelocity = new double[Dim];
21 for (int j = 0; j < randomVelocity.Length; ++j)
22 {
23 double lo = -1.0 * Math.Abs(maxX - minX);
24 double hi = Math.Abs(maxX - minX);
25 randomVelocity[j] = (hi - lo) * ran.NextDouble() + lo;
26 }
27 swarm[i] = new Particle(randomPosition, fitness, randomVelocity, randomPosition, fitness);
28 if (swarm[i].fitness < bestGlobalFitness)
29 {
30 bestGlobalFitness = swarm[i].fitness;
31 swarm[i].position.CopyTo(bestGlobalPosition, 0);
32 }
33 }
34 double w = 0.729;
35 double c1 = 1.49445;
36 double c2 = 1.49445;
37 double r1, r2;
38 while (iteration < numberIterations)
39 {
40 ++iteration;
41 double[] newVelocity = new double[Dim];
42 double[] newPosition = new double[Dim];
43 double newFitness;
44 for (int i = 0; i < swarm.Length; ++i)
45 {
46 Particle currP = swarm[i];
47 for (int j = 0; j < currP.velocity.Length; ++j)
48 {
49 r1 = ran.NextDouble();
50 r2 = ran.NextDouble();
51 newVelocity[j] = (w * currP.velocity[j]) +
52 (c1 * r1 * (currP.bestPosition[j] - currP.position[j])) +
53 (c2 * r2 * (bestGlobalPosition[j] - currP.position[j]));
54 if (newVelocity[j] < minV)
55 newVelocity[j] = minV;
56 else if (newVelocity[j] > maxV)
57 newVelocity[j] = maxV;
58 }
59 newVelocity.CopyTo(currP.velocity, 0);
60 for (int j = 0; j < currP.position.Length; ++j)
61 {
62 newPosition[j] = currP.position[j] + newVelocity[j];
63 if (newPosition[j] < minX)
64 newPosition[j] = minX;
65 else if (newPosition[j] > maxX)
66 newPosition[j] = maxX;
67 }
68 newPosition.CopyTo(currP.position, 0);
69 newFitness = ObjectiveFunction(newPosition);
70 currP.fitness = newFitness;
71 if (newFitness < currP.bestFitness)
72 {
73 newPosition.CopyTo(currP.bestPosition, 0);
74 currP.bestFitness = newFitness;
75 }
76 if (newFitness < bestGlobalFitness)
77 {
78 newPosition.CopyTo(bestGlobalPosition, 0);
79 bestGlobalFitness = newFitness;
80 }
81 }
82 }
83 }
84 catch (Exception ex)
85 {
86 }
87 }
Цикл начинается с присваивания случайного значения переменной ran, необходимой для расчета случайного значения коэффициентов r1 и r2 в формуле определения последующей скорости частицы vn(t + 1). Строка 5 инициализирует цикл try, в котором и осуществляется расчет всех параметров частиц на всех итерациях состояний всех моментов времени до появления некоторой ошибки расчета, реализуемой функцией catch (Exception ex). Инициализация роя частиц возложена на код строки 7, в котором при помощи внешнего класса Particle инициализируется переменная swarm, передающая в конструктор один-единственный заданный оператором параметр – numberParticles – количество частиц роя. Цикл строки 13 определяет положение текущей частицы в текущий момент времени. Строка 19 определяет ошибку текущего положения текущей частицы на каждой итерации времени моделирования посредством вызова внешнего метода ObjectiveFunction:
static double ObjectiveFunction(double[] k_T_b)
{
int k = 0;
double[] cur_error = new double[101];
double result = 1;
for (int n = 0; n < cur_error.Length; ++n)
{
cur_error[n] = 1;
}
for (double i = 0.1; i < 10.1; i=i+.1)
{
cur_error[k] = (2.46 * Math.Pow(10, -15) * Math.Exp(-5 * Math.Pow(10, -3)) * i + 7.68 * Math.Pow(10, -46) * Math.Exp(-1.81 * Math.Pow(10, 7)) - 1.62 * Math.Pow(10, -27) * Math.Exp(-1.67 * Math.Pow(10, 5) * i) - 26.6 * Math.Exp(-1 * i) + 12.9 + 13.7 * Math.Exp(-10 * i) * Math.Cosh(7.92 * i) + 13.8 * Math.Exp(-10 * i) * Math.Sinh(7.92 * i) - 7.11 * Math.Pow(10, -4) * Math.Exp(-8.57 * i) * Math.Cos(54.9 * i) + 2.84 * Math.Pow(10, -3) * Math.Exp(-8.57 * i) * Math.Sin(54.9 * i) - 8.92 * Math.Pow(10, -9) * Math.Cos(354 * i) -2.74 * Math.Pow(10, -7) * Math.Exp(-221 * i) * Math.Sin(354 * i)) - (1 * (k_T_b[0] - k_T_b[0] * Math.Exp(k_T_b[1] * i) * Math.Cos(k_T_b[2] * i) - 0.115 * Math.Exp(k_T_b[1] * i) * Math.Sin(k_T_b[2] * i)));
k = k + 1;
}
for (int j = 0; j < cur_error.Length; ++j)
{
result = Math.Abs(result * cur_error[j]);
}
return result;
}
Цикл строки 21 определяет массив значений скоростей каждой частицы. Строка 21 инициализирует частицу swarm с определенными ранее параметрами. Условие if строки 28 проверяет соответствие значения текущей ошибки положения частицы заданному. Далее инициализируются переменные расчета новых положения и скорости частицы c1, c2, r1, r2 и весовой коэффициент инерции w. Последующие циклы определяют новое положение и скорость текущей частицы и новую ошибку ее положения, в случае нового минимального значения которой последнее обновляется и ему присваивается значение текущей ошибки расчета.
Результаты исследования и их обсуждение
Задачей алгоритма служит определение коэффициентов α, β и γ аппроксимирующего звена в соответствии с его временной характеристикой:
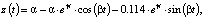
полученной посредством обратного преобразования Фурье:
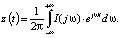
Функция ObjectiveFunction принимает в качестве параметра лишь один аргумент – массив значений переменных α, β и γ double[] k_T_b. В этом массиве содержатся все текущие значения решений поставленной задачи аппроксимации. Цикл for (double i = 0.1; i < 10.1; i = i+.1) производит определение текущей ошибки E итерации k посредством определения разности значения переходной характеристики эталонного звена и искомого аппроксимирующего звена, а также заполняет массив значений cur_error[k]. Переменная result определяет результирующую ошибку расчета на всех итерациях, возвращая рассчитанное значение в основной цикл try.
Итогом расчета является оптимальное положение частицы в трехмерном пространстве поиска решения. В данном случае аппроксимация указанной сложной передаточной функции реализуется массивом тысячи эпох перемещения частиц посредством звена вида (рис. 4):
Wтопл(s) =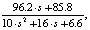 
которому соответствует временная характеристика вида
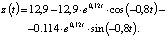
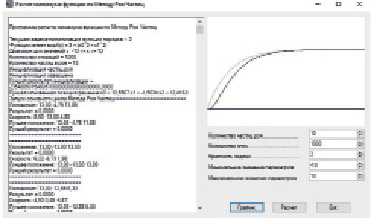
Рис. 4. Интерфейс программного обеспечения для поиска минимума по МРЧ
Заключение
Рассмотренная структура предназначена для аппроксимации сложных звеньев и подтверждает допустимую возможность определения аппроксимирующего апериодического звена второго порядка для сложного динамического звена. Как видно из предоставленного результата, данный метод не лишен недостатков. Стоит отметить уже обозначенный выше недостаток – вероятность определения неистинного минимума, что косвенно подтверждается и в данном случае. Начало переходного процесса полученного звена недостаточно корректно соответствует эталонному сложному звену. Однако здесь следует сделать замечание относительно возможностей описанного алгоритма. Так как поиск решения ведется в трехмерном пространстве, то неизменным остается коэффициент -0,114 при отрицательной части полинома. По этой причине очевидна дальнейшая необходимость модификации описанной структуры с целью минимизации ошибки расчета и поиска решения на пространстве четырех измерений.